我的题解(3)-求最小循环节(KMP,POJ2406)
KMP(烤馍片)算法想必大家都会吧,这次让我们来做一道题——求最小循环节。
先上题,题目大意是这样的(我对原题进行了一些改动):给你一个字符串s(|s|≤1,000,000),求其最小循环节。最小循环节指有一s的子串a,s=aaa...a,也就是共n个a可顺序拼成原串s(原题是说s=a^n)。
样例:
1.abcd 最小循环节为其本身
2.aaaa 最小循环节为a
3.ababab 最小循环节为ab
很多大佬会说:这不是弱智题吗?那你就错了,请看我慢慢道来。
首先看到这道题,第一反应应该就是哈希(划掉)KMP,我们对它进行一个变形。
从哪里入手呢?想想next数组?
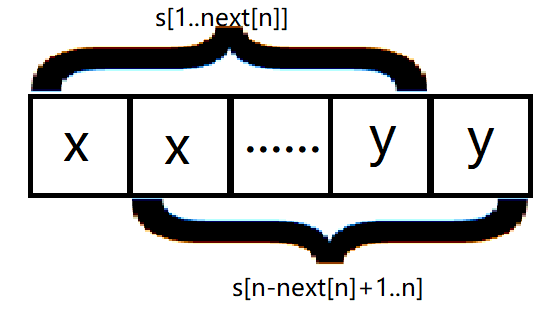
首先,我们看看next数组的定义
next[i]=max{k
通俗地讲,next[i]表示s的前i个字符构成的子串t中t的前缀与后缀相等的最长长度。
这个大家都懂的吧,如果还不知道KMP,那么先学学吧。
看了这个,大家是否有什么感觉了呢?next...相等...前缀与后缀...循环节!只有前缀与后缀相等,这个前缀(或后缀)才有可能是循环节!
不错,其实我们根本就不用考虑KMP的匹配,用next数组就可以求出答案。
讲到这里,一般的解题博客就开始贴代码了,emmm...要不我也贴个代码?
#include
#include
#include
using namespace std;
char s[1000001];
int Next[1000001],lens,nextN;
void getNext(){
int k=0;
Next[1]=0;
for(int i=2;i<=lens;i++){
while(k&&s[k+1]!=s[i]) k=Next[k];
if(s[k+1]==s[i]) k++;
Next[i]=k;
}
}
int main(){
while(1){
scanf("%s",s+1);
if(s[1]=='.') return 0;
lens=strlen(s+1);
memset(Next,0,sizeof(Next));
getNext(),nextN=lens-Next[lens];
if(lens%nextN==0) printf("%d\n",lens/nextN);else
printf("1\n");
}
return 0;
} (注:原题代码)
(前方高能)
求next数组大家一定很清楚,但是
if(lens%nextN==0) printf("%d\n",lens/nextN);else
printf("1\n");
嗯,这就是这道题的难点!
我们来理解一下。为了方便,我们令|s|=n。
这两行代码的意思是,若n-next[n]可以整除n,则next[n]为最小循环节,否则整个串就是最小循环节。
看到这里,如果你想问"为什么"或你只有一个草率的理由,你就是不懂这道题!
证明!!!
为了方便,我们不妨令nextN=n-next[n].
我们要证明的命题有:
1.当nextN|n时,nextN是一个循环节的长度;
2.当nextN|n时,没有比nextN更小的循环节长度;
3.当nextN不整除n时,不存在比nextN更大的循环节长度(原串除外)。
我们先证第一个。
根据next的定义,s的前next[n]个和后next[n]个是相等的,也就是s[1..next[n]]=s[nextN+1..n]。
我们取next[n]的前nextN个字符。
根据这些前提,可以推出s[1..nextN]=s[nextN+1..2nextN],s[n-2nextN+1..n-nextN]=s[n-Next[n]..n]。
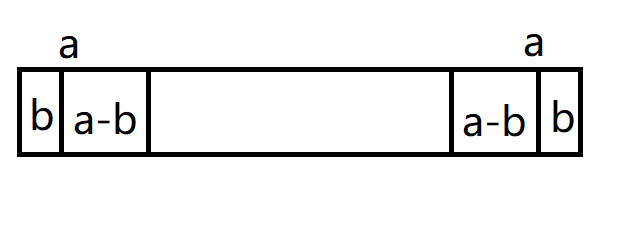
正是因为这个,我们可以将s设为xx...yy(注:中间一段是不确定的)。
我们继续取第二段长度为nextN的。
可以推出s[nextN+1..2nextN]=s[2nextN+1..3nextN],s[n-3nextN+1..n-2nextN]=s[n-2nextN+1..n-nextN]。
我们将前面的等式连等起来,可以将s进一步设为xxx...yyy(注:中间一段是不确定的)。
像这样一直推下去,直到去next[n]的最后nextN个字符。
s[n-2nextN+1..n-nextN]=s[n-Next[n]..n],s[1..nextN]=s[nextN+1..2nextN]。
到这里,我们就完整地得到——x=y!
(注:其实当x与y交叉时,就可以推出;特殊情况:当n为偶数且nextN=n/2时,显然推出nextN是循环节长度。)
我们想想,能推出这样的结论的前提是什么?对,是nextN|n。
只有nextN|n时,才能根据上述方法推到最后,不然,字符会错位哦~就不相等了!
我们——终于——证完了——第一个命题- -(如果看不懂,自己举个栗子吧,如ababababab)
第二个命题略简单哦~
开始证第二个,用反证。
若存在一个比nextN更小的循环节长度p,则我们可列出一不等式:
nextN>p⇒n-next[n]>p⇒n-p>next[n]
∵p是循环节,∴n-p可以是next[n]的更大长度。这时就与next的定义-最大矛盾了!
所以next[n]必须是最大的,也就是nextN必须是最小的循环节长度。
我们开始证第三个命题。
首先,我们需要找到所有可能为s的循环节的子串长度。
令集合X={next[n],next[next[n]],...,0},则根据next的定义,只有n-X[i](1≤i≤|X|)才有可能为循环节的长度。
好,根据假设,(n-X[1])不整除n,也就是nextN不是可行的循环节。
我们这次使用数学归纳法来证明——除了n本身,其他的长度都不可行。
我们取b=n-X[i],a=n-X[i+1],b
首先,i以及i之前的长度都是不可行的,我们就先取出i吧,也就是b不整除n。
假设a|n,那么我们可以类似地使用命题(1),证出a也是一个可行的循环节长度。
则显然,a-b也是一个可行的循环节长度;接着,若a-b
这样以此类推,我们最后发现这是求最大公因数的更相减损法!(若不了解更相减损法,就先去学学吧)
最终,我们得到gcd(a,b)为循环节长度,因为gcd(a,b)≤b
但是gcd(a,b)≤b啊!假设里不是说“i以及i之前的长度都是不可行的”吗?
所以,我们找到了一个更小的循环节长度,与假设出现矛盾!
这时,我们就得出a不能整除n了。根据此方法类推,我们一直推到X的最后一个元素——0.
由于n-0=n,而n绝对是s的循环节长度(n就是s本身的长度,只需1个循环节便可以表示出整个字符串)
所以,当nextN不整除n时,最小循环节就是n。
证完这三个命题,我们才算完成了这道题目!
根据原题意(POJ2406),我们要算出最小循环节的个数,那么用最小循环节的长度去除一下n即可。
在简单的两行代码
if(lens%nextN==0) printf("%d\n",lens/nextN);else
printf("1\n");
中,奥秘无穷!
结语:这就是编程,真正的大佬是对每一步都精打细算的!
emmmm...然而我只是个蒟蒻,希望大家多多指出错误哦~