最近看了一篇颇有趣的并查集文章,放在这里推荐一下,顺便自己也想总结一下。
http://blog.csdn.net/dellaserss/article/details/7724401/
并查集:
判断图是否连通,以及有几个连通分量。
其实现方法,却是用树来进行查找。
原理:
把每一个连通分量都看做一个树,判断两个结点是否在一个连通分量中(即是否属于一棵树),需要查找是否有同一个根节点,如果是,则是同一个连通分量,不是,则不是同一个连通分量。
实现方法:
每一个结点都记录其双亲结点,双亲结点再记录自己的双亲结点,直到根节点,其记录的双亲结点是自己的下标。
int find(int x)
{
int r=x;
while (pre[r ]!=r)
r=pre[r ] ;
return r ; }
初始化方案:
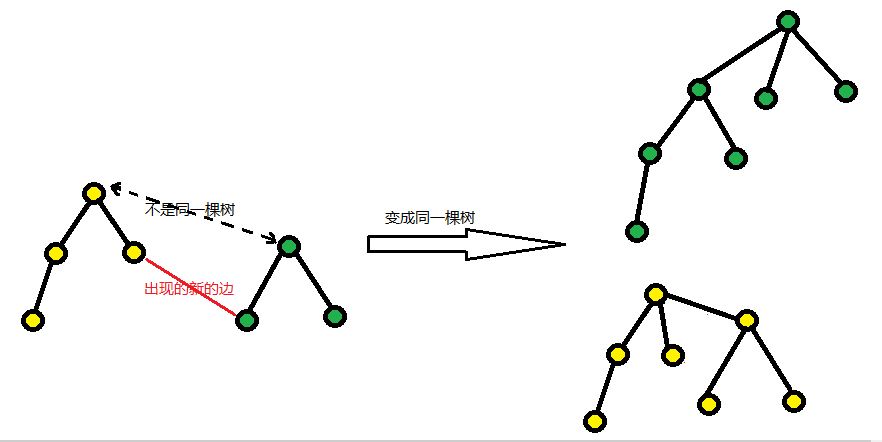
可以把每一个结点的pre值都记录为自己,每当出现一条边,如果两个结点属于不同的连通分量,边的一个结点的根节点就等于另一个结点的根节点,如果觉得不容易理解,看图解:
最后结合成的两种树都是正确的合并方式,可以根据自己的意愿结合。
void join(int x,int y)
{
int fx=find(x),fy=find(y);
if(fx!=fy)
pre[fx ]=fy;
}
优化:
每次判断两个结点是否是同一个联通分量都需要从该结点开始迭代到根节点,为了节省时间复杂度,可以让每一个结点都记录所在树的根节点,当出现树的合并时,每向上迭代寻找一次双亲结点就重新赋值一次:
r=find(x);
int i=x,j;
while(pre[i]!=r)
{
j=pre[i];
pre[i]=r;
i=j;
}
在实现的时候送上一道经典的例题和解法,需要注意的是在解题当中如何初始化pre数组和对数组的赋值过程原理。
实现:
#include int pre[1000 ];
int find(int x)
{
int r=x;
while (pre[r ]!=r)
r=pre[r ];
int i=x; int j;
while(i!=r)
{
j=pre[i ];
pre[i ]=r;
i=j;
}
return r;
}
int main()
{
int n,m,p1,p2,i,total,f1,f2;
while(scanf("%d",&n) && n) //读入n,如果n为0,结束
{ //刚开始的时候,有n个城镇,一条路都没有 //那么要修n-1条路才能把它们连起来
total=n-1;
//每个点互相独立,自成一个集合,从1编号到n //所以每个点的上级都是自己
for(i=1;i<=n;i++) { pre[i ]=i; } //共有m条路
scanf("%d",&m); while(m--)
{ //下面这段代码,其实就是join函数,只是稍作改动以适应题目要求
//每读入一条路,看它的端点p1,p2是否已经在一个连通分支里了
scanf("%d %d",&p1,&p2);
f1=find(p1);
f2=find(p2);
//如果是不连通的,那么把这两个分支连起来
//分支的总数就减少了1,还需建的路也就减了1
if(f1!=f2)
{
pre[f2 ]=f1;
total--;
}
//如果两点已经连通了,那么这条路只是在图上增加了一个环
//对连通性没有任何影响,无视掉
}
//最后输出还要修的路条数
printf("%d\n",total);
}
return 0;
}
在对并查集进行了学习后,不妨拿出一道例题,进行深一步的利用:
分析题意:
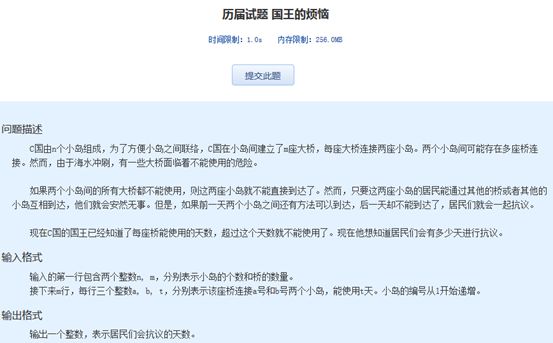
题目所给定的是两个小岛在有一天突然由连通变成不连通的时候进行抗议一天,求解共抗议多少天。
逆序思维:
将时间从大到小排序,可以知道小岛从开始的不连通渐渐连通,而我们要求得是在加上一座桥的时候两个小岛从连通到不连通的数量。
故在加入一座桥时可以分为两种情况:
1、判断两个小岛是否连通,如果是,那么加上桥以后还连通,所以该桥毁掉后居民不会抗议。
2、如果不连通,那么在这天居民将会举行游行,游行天数加一。
之所以将时间由大到小排序后再进行判断,是为了解决以下问题:
1、可能有两座桥是在同一天坏的且坏掉后都会进行抗议,那么为了统计重复的天数还要另外开辟数组且每次都要遍历查重。
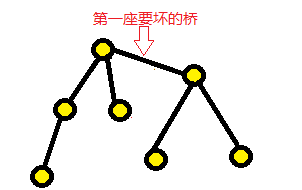
2、如果是从时间由小到大排的,那么需要解决的问题是:首先从第一座要坏的桥开始,初始化所有的桥,建立一棵或多棵树,然后从第一座桥开始判断,是否两个小岛连通。需要注意的是,该树的生成已经是在加入了该座桥的情况下产生的,可以参考之前的图片:
想要知道是否加上该座桥后连通,需要做的只能是在不建立这座桥之前进行建树,而按照从小到大排序建树的规则是不允许做到的,所以只有按照从大到小排序建树。
在理解到这里的情况下,就可以编码解决问题了:
#include
#include
#include
#include
using namespace std;
struct node
{
int x,y,d;
} s[100000+5];
int n,f[10000+5];
bool cmp(node a,node b)
{
return a.d>b.d;
}
void Set()
{
for (int i=1; i<=n; i++)
f[i]=i;
}
int Find(int x)//查找根节点
{
if (f[x]==x)
return x;
return f[x]=Find(f[x]);
}
bool Union(int x,int y)
{
x=Find(x);
y=Find(y);
if (x!=y)
{
f[x]=y;
return 1;
}
return 0;
}
int main()
{
int m;
while (~scanf("%d%d",&n,&m))
{
for (int i=1; i<=m; i++)
{
scanf("%d%d%d",&s[i].x,&s[i].y,&s[i].d);
}
sort(s+1,s+m+1,cmp);
Set();
int pre=-1,ans=0;//表示前一次是在第几天进行反抗的
for (int i=1; i<=m; i++)
{
int way=Union(s[i].x,s[i].y);//way=0表示之前有桥,不需要在建桥
if (way==1&&s[i].d!=pre)
{
ans++;
pre=s[i].d;
}
}
cout<