视觉SLAM笔记--第7篇: 单目相机位姿估计流程

参考书籍

参考书籍：《视觉SLAM十四讲》 高翔博士

整体流程

1. 坐标系变换

已知：匹配的像素点对$(u,v)，(u^{{}^{\prime }},v^{{}^{\prime }})$，相机内参矩阵$K$
求解：相机归一化坐标$(X^{{}^{\prime }},Y^{{}^{\prime }},1)$
通过相机与像素间的坐标变换关系，可以得到下面公式：
$$\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{X}^{{}^{\prime }}\\ Y^{{}^{\prime }}\\ 1\end{array}\right]$$表示像素坐标与相机归一化平面坐标的变换关系。

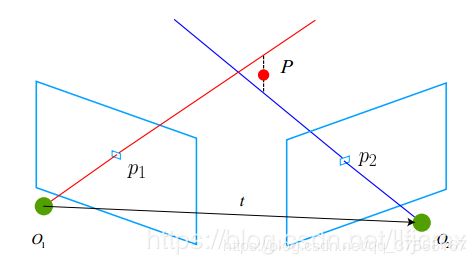
2. 对极约束

利用对极约束关系，具体推导可参见博客，利用求得的相机归一化坐标$x_1，x_2$，可以求解基础矩阵和本质矩阵：
$$x_{2}E{x}_1=0$$分解$E$便可以得到变换矩阵$R,t$，注意，由于E(本质矩阵)本身具有尺度等价性,它分解得到的$R、t$也有一个尺度等价性。

3. 单目初始化

在单目视觉中，我们对两张图像的t进行归一化，相当于固定了一个尺度。虽然我们不知道它的实际长度是多少，但是我们可以以这时的 $t$为单目1，计算相机运动和特征点的3D位置，这一步称为单目SLAM的初始化。

通常把 $t$ 进行归一化，让它的长度等于1.

初始化的两张图片必须要有一定程度的平移，而后的轨迹和地图都将会以这一步的平移为单位。单目初始化不能只有纯旋转，必须要有一定程度的平移，如果没有平移，单目将无法初始化。

4. 三角测量

按照对极几何中的定义，如果设$x_1,x_2$为两个特征点的归一化坐标，于是有下列关系式：
$$s_1{x}_1=s_2{x}_{2}R+t$$已知：坐标系$o到o_1$的变换矩阵$R、t$归一化坐标$x_1,x_2$，现在要求的就是两个特征点的深度$s_1,s_2$

左乘$[x_1{]}_{\times }$可得$s_1[x_1{]}_{\times }{x}_1=0$：
$$s_2[x_1{]}_{\times }{x}_{2}R+[x_1{]}_{\times }t=0$$可以解出$s_2$, 将其带入原来的式子可解出$s_1$.
但是，由于噪声的存在，我们求出来的R,t不一定能够使得上式精确等于0，因此在实际情况中，更常见的做法是求最小二乘解而不是零解。

5. 求解空间3D坐标

已知：像素点坐标$(u,v)$，相机内参矩阵$K$，像素点的空间深度$s$
求解：相机坐标$(X,Y,Z)$
通过相机与像素间的坐标变换关系，可以得到下面公式：
$$s\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}X\\ Y\\ Z\end{array}\right]$$
利用计算得到的相邻两帧相机变换关系$R，t$ 以及相机坐标$P_c=(X,Y,Z)$，可以求解世界坐标$P_w$
$$P_c=R\ast P_w+t$$注意：这是以第一帧相机原点作为世界坐标系的原点进行求得，后面由于相机在不断移动，因此相机间的变换矩阵在不断改变，通过变换矩阵累乘的方式将相机坐标变化为世界坐标。

重点：
如果要计算第$n$ 个相机下，其相机坐标到世界坐标的变换，需要用以下的公式计算：

已知：第一帧相机到第二帧相机的变换矩阵$T_{12}$（世界坐标到相机坐标系变换就很），第二帧相机到第三帧相机的变换矩阵$T_{23}$，以此类推，第$n-1$帧相机到第$n$帧相机的变换矩阵$T_{(n-1)n}$， 第$n$帧相机下的相机坐标$P_c^{(n)}$

求解：第$n$帧相机下的世界坐标$P_w^{(n)}$

$$P_w^{(n)}=T_{12}\ast T_{23}\ast ......\ast T_{(n-1)n}\ast P_c^{(n)}$$其中$T_{12}\ast T_{23}\ast ......\ast T_{(n-1)n}\ast P_c^{(n)}$就是相机到世界坐标系的欧式变换矩阵，是重投影误差的初始值。

6. 最小化重投影误差

已知：3D空间坐标$P_i$，及其投影像素坐标$u_i$，相机的初始位姿$T$(相机到世界坐标系的变换矩阵)，可以由第(5)步得到。

求解目标函数：
$$T^{\ast }=\underset{T}{\mathrm{argmin}}\frac{1}{2}||u_i-\frac{1}{s_i}KT{P}_i|{|}^2$$根据高斯牛顿法，可得：
$$e(x+\Delta x)=e(x)+J^T\Delta x$$其中$J^T$表示目标函数(误差)关于$T$的一阶导数，雅可比矩阵，根据链式法则可以将其分解如下：

其中$P^{{}^{\prime }}$表示相机坐标，因此可以将求解的世界坐标转换为对相机坐标求导。

可以得雅可比矩阵：


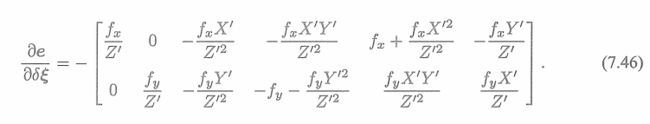
通过高斯牛顿或者LM法不断优化重投影误差，便可以得到较为准确的位姿。