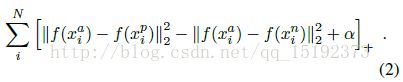传统的基于CNN的人脸识别方法为:
1. 利用CNN的siamese网络来提取人脸特征
2. 然后利用SVM等方法进行分类
facnet亮点
1. 利用DNN直接学习到从原始图片到欧氏距离空间的映射,从而使得在欧式空间里的距离的度量直接关联着人脸相似度;
2. 引入triplet损失函数,使得模型的学习能力更高效。
部分结果展示:
而这篇文章中他们提出了一个方法系统叫作FaceNet,它直接学习图像到欧式空间上点的映射,其中呢,两张图像所对应的特征的欧式空间上的点的距离直接对应着两个图像是否相似。
图1
这是一个简单的示例,其中图中的数字表示这图像特征之间的欧式距离,可以看到,图像的类内距离明显的小于类间距离,阈值大约为1.1左右。
实现
这篇文章中,最大的创新点应该是提出不同的损失函数,直接是优化特征本身,用特征空间上的点的距离来表示两张图像是否是同一类。网络结构如下:
图2
上图是文章中所采用的网络结构,上图步骤可以描述为:
1.前面部分采用一个CNN结构提取特征,
2.CNN之后接一个特征归一化(使其特征的||f(x)||2=1,这样子,所有图像的特征都会被映射到一个超球面上),
3.再接入一个embedding层(嵌入函数),嵌入过程可以表达为一个函数,即把图像x通过函数f映射到d维欧式空间。
4.此外,作者对嵌入函数f(x)的值,即值阈,做了限制。使得x的映射f(x)在一个超球面上。
5.接着,再去优化这些特征,而文章这里提出了一个新的损失函数,triplet损失函数(优化函数),而这也是文章最大的特点所在。
Triplet Loss(三元组损失函数):
以下是Triplet损失函数的原理(Triplet翻译为三元组):
思想:
什么是Triplet Loss呢?故名思意,也就是有三张图片输入的Loss(之前的都是Double Loss或者是 SingleLoss)。
本文通过LDA思想训练分类模型,使得类内特征间隔小,类间特征间隔大。为了保证目标图像 与类内图片(正样本)特征距离小,与类间图片(负样本)特征距离大。需要Triplet损失函数来实现。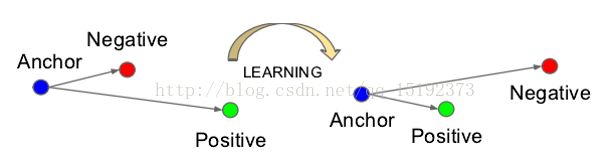
根据上文,可以构建一个约束条件:
把上式写成损失(优化)函数,通过优化(减小)损失函数的值,来优化模型。损失函数为:
Triplet Selection(generate)
在上面中,如果严格的按照上式来进行学习的话,它的T(穷举所有的图像3元组)是非常大的。
举个例子:在一个1000个人,每人有20张图片的情况下,其T=(1000*20)*19*(20*999)(总图片数*每个图片类内组合*每个图片类间组合),也就是O(T)=N^2 ,所以,穷举是不大现实的。那么,我们只能从这所有的N^2个中选择部分来进行训练。现在问题来了,怎么从这么多的图像中挑选呢?答案是选择最难区分的图像对。
给定一张人脸图片,我们要挑选:
1.一张hard positive:即在类内的另外19张图像中,跟它最不相似的图片。(正样本里面最差的样本)
2.一张hard negative:即在类间的另外20*999图像中,跟它最为相似的图片。(负样本里面最差的样本)
挑选hard positive 和hard negative有两种方法,offline和online方法,具体的差别只是在训练上。
问题描述:为了确保模型快速收敛,选择违反公式1的约束条件的三元组(损失函数的负样本,与前面的类间图片表示的“负样本”不一样)是至关重要的。这意味着给定![]() ,我们需要:
,我们需要:
1.选择一个![]() ,使得
,使得![]()
2.选择一个![]() ,使得
,使得 ![]()
解决方案:
在整个训练集上寻找argmax和argmin是困难的。如果找不到,会使训练变得困难,难以收敛,例如错误的打标签和差劲的反映人脸。因此需要采取两种显而易见的方法避免这个问题:
1.离线更新三元组(每隔n步)。采用最近的网络模型的检测点 并 计算数据集的子集的argmin和argmax(局部最优)。
2.在线更新三元组。在mini-batch上 选择不好的正(类内)/负(类间)训练模型。(一个mini-batch可以训练出一个子模型)
本文中采用上述第二种方法。本文中,采用以下方法:
1.使用大量 mini-batch,从而得到几千个不好的训练模型。
2.计算mini-batch上的argmin和argmax。
总结:以上所有过程博主概括为:为了快速收敛模型-->需要找到训练的不好的mini-batch上的差模型(负样本)-->从而找到 不满足约束条件/使损失增大 的三元组
在本文中,训练集的每个mini-batch包含:
1. 每个身份的40个人脸
2. 随机放一些负样本人脸
实际采用方法:
1.采用在线的方式 (作者说,在线+不在线方法结果不确定)
2.在mini-batch中挑选所有的anchor positive 图像对 (因为实际操作时,发现这样训练更稳定)
3.依然选择最为困难的anchor negative图像对 (可以提前发现不好的局部最小值)
特殊情况:
选择最为困难的负样本,在实际当中,容易导致在训练中很快地陷入局部最优,或者说整个学习崩溃f(x)=0 //我在CNN学习的时候也经常会遇到这个问题,不过我的是f(x)=1。为了避免这个问题,在选择negative的时候,使其满足式(3):
左边:Positive pair的欧式距离右边:negative pair的欧式距离。把这一个约束叫作semi-hard (半序关系)。因为虽然这些negative pair的欧式距离 远小于 Positive pair的欧式距离,但是 negative pair的欧式距离的平方 接近于Positive pair的欧式距离的平方。
深度网络结构
最优化算法:
1. SGD+标准BP
2. AdaGrad
起始的学习率:0.05 (之后逐渐递减,直到模型收敛)
训练时间:在cpu集群上训练1000-2000 h,从500 h开始,loss大幅减少。
参数:设置为0.02
网络结构:(均使用修正的线性单元作为非线性激活函数)
1. 左边是ZF-Net。原文描述如下:
步长不为1的时候,输入维数又很大的时候,该怎么计算,经过自己的研究得出公式(池化也是一样计算):
input_size: 输入维数大小
filter_size: 卷积核大小
stride: 步长
feature map = [(input_size - filter_size+ stride) /stride] ;;上取整,边界不丢弃(加上一个stride再除以stride,因为最后1次滑动也算入)
输入层:224*224像素,3颜色通道
1st隐藏层:卷积。每个颜色通道96个滤波器,大小7*7,x和y方向上的步长均为2。卷积得到110*110的特征图( 特征图边长=(224-7+2)/2)--> 经过 一个修正的线性单元(Relu, 图中未显示)-->池化。3*3的最大池化,x和y方向上的步长均为2。池化得到50*50的特征图( 特征图边长=(110-3+2)/2) )
BN层:对比和归一化这96个特征层
2345层:原理同上
67层:全连接层,把第5层的特征图转化成一维向量。
8层:softmax层,把输出值归一化( soft(软化)+max(最大值归1,其余归0) )
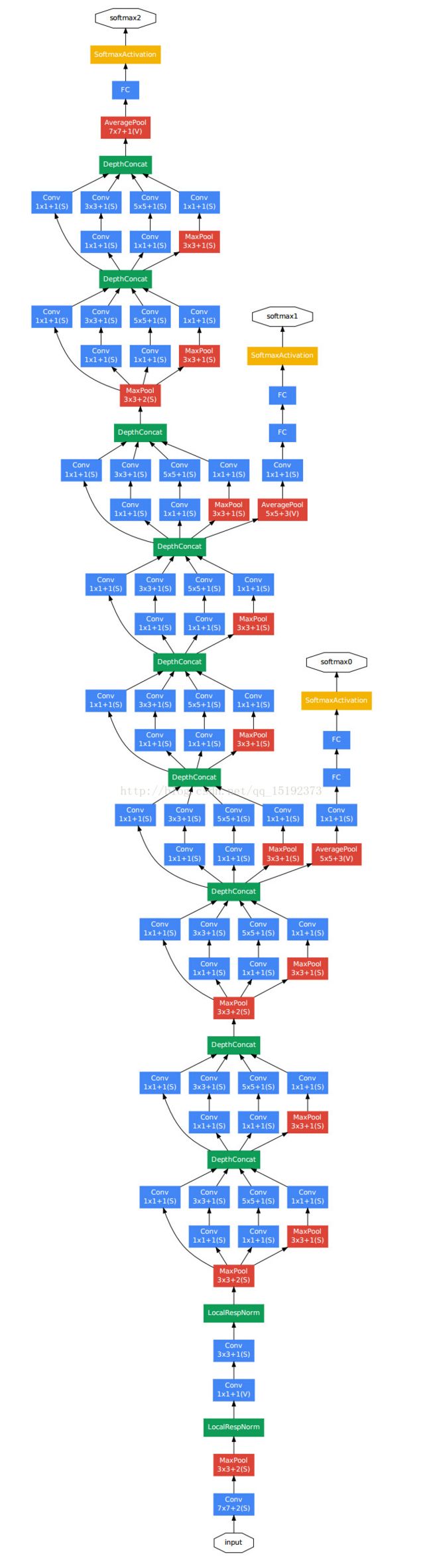
2.右边是GooLeNet。层数更多,参数更少。网络结构如下:
对上图做如下说明:
1 . 显然GoogLeNet采用了模块化的结构,方便增添和修改;
2 . 网络最后采用了average pooling来代替全连接层,想法来自NIN,事实证明可以将TOP1 accuracy提高0.6%。但是,实际在最后还是加了一个全连接层,主要是为了方便以后大家finetune;
3 . 虽然移除了全连接,但是网络中依然使用了Dropout ;
4 . 为了避免梯度消失,网络额外增加了2个辅助的softmax用于向前传导梯度。文章中说这两个辅助的分类器的loss应该加一个衰减系数,但看caffe中的model也没有加任何衰减。此外,实际测试的时候,这两个额外的softmax会被去掉。
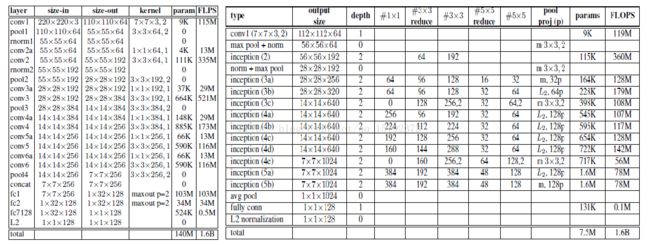
下面是文中实验用到的一些网络模型:
NN1:ZF-Net(Zeiler&Fergus),在前几个卷积层中加入了1*1*d的卷积层,有效的减小了参数的个数。但和GoogleNet相比,参数量还是很大。
NN2:GooleNet。如图6。与原模型主要区别在于:
1.使用的是L2池化而不是max池化。
2.池化的卷积核大小一般是3*3(除了最后那个平均池化),并且并行于每个输入模块里的卷积模块。
如果在1*1,3*3,5*5池化后有维度下降,那么把它们连接起来作为最后的输出。
NNS1:剪裁后的GooleNet。为了使得模型可以嵌入到移动设备中,本文中也对模型进行了裁剪。NNS1即只需要26M的参数和220M的浮点运算开销。
NNS2:剪裁后的GooleNet。NNS2则只有4.3M的参数和20M的浮点运算量。
NN3:GooleNet。与NN2结构一样,但输入图片大小只有160*160。这样极大幅度的降低了对CPU的需求。
NN4:GooleNet。与NN2结构一样,但输入图片大小只有96*96。这样极大幅度的降低了对CPU的需求。