视觉惯性里程计（VIO）

视觉惯性里程计（VIO）

本文是 Forster et al. 的阅读笔记，自己补充了一点基于鱼眼相机的噪声传递内容。

概述

使用视觉和惯性部件可以分别定位目标。双目相机通过在像素平面捕捉目标、确定相差从而计算出目标物体的三维坐标，对于低速运动的目标能够较为准确地定位；然而对于高速（或运动状态剧烈改变）的物体这种定位方式甚至难以运行，而即使低速状态也无法避免光照或背景干扰的影响。使用搭载在目标物体上的惯性部件（如 IMU 或磁力仪等）能够高速、实时地测量物体的运动状态（或运动状态的改变），对于视觉方法难以处理的快速运动或运动状态剧烈变化等情况具有良好的适应性。不过基于微机电系统（MEMS, Micro-Electro-Mechanical System）的惯性部件都不可避免的存在系统偏差（bias），又因为惯性部件直接测量到的是运动量（如角速度）或运动改变量（如加速度），为了得到物体位置或姿态必须对其进行时间积分，这将导致上述偏差不断累积最终让结果无法使用。

融合视觉和惯性部件将能够大幅度提升定位的准确性和稳定性。不过因为两套方法测量的数据类型（视觉测量物体在像素平面上投影的坐标，而惯性部件测量的是物体的三维加速度和转动角速度）和测量速率（视觉受制于相机帧率和图像处理速度采样率只能达到几十帧每秒，惯性部件则可以轻松达到数百甚至上千帧每秒的采样率）都存在较大差异，对两者数据进行融合时无论是将惯性部件测量到的运动量转换为物体坐标（积分中bias累积）或是把视觉量转变为运动量（微分时由于定位偏差导致计算出的加速度大幅度震荡）都会引入额外的误差，这让融合变得不是很简单。

一般来说，比起对视觉量做微分，融合中通常选择将惯性部件测量到的运动量积分为物体坐标后与视觉量进行融合。如此需要在积分中排除掉（未知的）系统偏移量（bias）的影响，或是用最优化的方法同时估计出偏移量和待求物体的坐标。若使用最优化的思路，参考 SLAM 中 VIO（Visual-Inertial Odometry）的方法，通过计算并最大化物体位置和姿态坐标在视觉、惯性测量数据下的后验概率给出位姿坐标的最优解，从而实时跟踪目标位置。

下述推导中我们假设相机相对世界坐标的位姿固定不变，因此排除了物体到相机坐标系间的转换带来的误差。更一般的情况需要首先通过 SLAM 方法确定出相机位姿再与物体上惯性器件进行融合（或使用最优化方法同时完成目标物体定位与 SLAM）。

惯性元件和预积分

这里暂时忽略惯性器件的初始化问题，仅考虑视觉和惯性器件在运行过程中的最优化问题。根据文献 Forster et al. 的方法，可以在固定于物体上的坐标系内进行积分从而消除初始状态未知带来的影响。

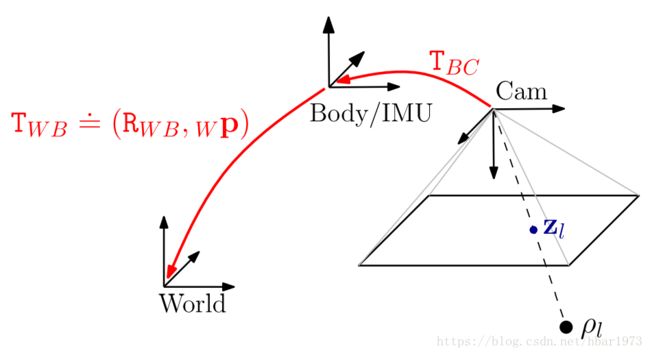
具体来说，上图中假设目标物体（IMU）的坐标系为 B(ody) 系，世界坐标系为 W(orld) 系，忽略地球自转因此 W 系是一个惯性系，而 B 系中IMU的测量值 Bω~WB(t) B ω ~ W B ( t ) （角速度）和 Ba~(t) B a ~ ( t ) （加速度）满足：

Bω~WB(t)Ba~(t)=BωWB(t)+bg(t)+ηg(t),=RTWB(t)[Wa(t)−Wg]+ba(t)+ηa(t). B ω ~ W B ( t ) = B ω W B ( t ) + b g ( t ) + η g ( t ) , B a ~ ( t ) = R W B T ( t ) [ W a ( t ) − W g ] + b a ( t ) + η a ( t ) .

其中 RWB R W B 是 B 系到 W 系的转动， BωWB(t) B ω W B ( t ) 和 Ba(t) B a ( t ) 是IMU 感受到的真实角速度和加速度（未知）， bg(a) b g ( a ) 是惯性器件的系统偏差， ηg(a) η g ( a ) 是噪声信号，而 Wg W g 则是重力加速度。

IMU 在 W 系满足运动学方程

R˙WB=RWBBω∧WB,Wv˙=Wa,Wp˙=Wv. R ˙ W B = R W B B ω W B ∧ , W v ˙ = W a , W p ˙ = W v .

其中 (⋅)˙ ( ⋅ ) ˙ 代表对时间求导， (⋅)∧ ( ⋅ ) ∧ 是矢量的反对称化算符， Wv W v 和 Wp W p 是 W 系中物体的速度和三维坐标。对上述运动学方程在两次测量的间隔 [t,t+Δt] [ t , t + Δ t ] 内积分并代入第一组方程后得到目标位置和运动学量与 IMU 测量值的关系（不造成误解的情况下省略下标）：

R(t+Δt)v(t+Δt)p(t+Δt)===R(t)Exp{[ω~(t)−bg(t)−ηgd(t)]Δt},v(t)+gΔt+R(t)[a~(t)−ba(t)−ηad(t)]Δt,p(t)+v(t)Δt+12gΔt2+12R(t)[a~(t)−ba(t)−ηad(t)]Δt2.(1)(2)(3) (1) R ( t + Δ t ) = R ( t ) E x p { [ ω ~ ( t ) − b g ( t ) − η g d ( t ) ] Δ t } , (2) v ( t + Δ t ) = v ( t ) + g Δ t + R ( t ) [ a ~ ( t ) − b a ( t ) − η a d ( t ) ] Δ t , (3) p ( t + Δ t ) = p ( t ) + v ( t ) Δ t + 1 2 g Δ t 2 + 1 2 R ( t ) [ a ~ ( t ) − b a ( t ) − η a d ( t ) ] Δ t 2 .

其中 Exp 定义为李代数到转动矩阵的变换（详见文献 Forster et al. 第三节），此外由于对时间进行了离散化，噪声信号重新标记为 ηgd(ad) η g d ( a d ) ，对于白噪声其期望值不变、方差变为 Cov[ηgd(ad)(t)]=1ΔtCov[ηg(a)(t)] C o v [ η g d ( a d ) ( t ) ] = 1 Δ t C o v [ η g ( a ) ( t ) ] 。

预积分

因为 IMU 和照相机采集的信号类型不同且采样率差异巨大（下图），为了同步两者的数据一般需要在图片的两帧之间对 IMU 数据进行积分。图里假设已经同步了初始的图像和 IMU 数据，另外因为不是每帧图像上都能成功捕捉并定位到目标物体，因此我们选取能够定位到物体的帧为关键帧（Keyframes）并计算 IMU 数据在关键帧之间的积分。

预积分处理了上述积分里的两个问题：

• 第一，实际运行时需要不断地对 IMU 的初始信号进行调整以获得接近真实的定位，然而直接对 IMU 数据积分的积分值大小与初始值有关，因此每做一次调整都需要重新进行积分；
• 第二，由于积分导致的非线性，最优化 IMU 初始值必须使用非线性的算法。

预积分将 IMU 的积分中与初始值无关的部分分离避免了重复计算，剩下的部分与积分初始值呈简单的（线性）关系方便优化。（预积分的物理意义是坐标系变换，通过在初始时刻的非惯性系中进行积分，从而排除了初始时刻的影响）

如图中所示，计算关键帧 [ti,tj] [ t i , t j ] 间物体位姿的变化时将积分分解为其间所有 Δt Δ t 上的积分之和（每个 Δtk Δ t k 可能不同）。则初始值（ t=ti t = t i 时刻的值）无关的预积分值可以写为：

ΔRijΔvijΔpij≐RTiRj=∏k=ij−1Exp[(ω~k−bgk−ηgdk)Δt],≐RTi(vj−vi−gΔtij)=∑k=ij−1ΔRik(a~k−bak−ηadk)Δt,≐RTi(pj−pi−viΔtij−12gΔt2ij)=∑k=ij−1[ΔvikΔt+12ΔRik(a~k−bak−ηadk)Δt2]. Δ R i j ≐ R i T R j = ∏ k = i j − 1 E x p [ ( ω ~ k − b k g − η k g d ) Δ t ] , Δ v i j ≐ R i T ( v j − v i − g Δ t i j ) = ∑ k = i j − 1 Δ R i k ( a ~ k − b k a − η k a d ) Δ t , Δ p i j ≐ R i T ( p j − p i − v i Δ t i j − 1 2 g Δ t i j 2 ) = ∑ k = i j − 1 [ Δ v i k Δ t + 1 2 Δ R i k ( a ~ k − b k a − η k a d ) Δ t 2 ] .

其中 (⋅)i≐(⋅)(ti) ( ⋅ ) i ≐ ( ⋅ ) ( t i ) ，且有 Δtij≐tj−ti Δ t i j ≐ t j − t i 。公式中三个预积分量 ΔRij Δ R i j 、 Δvij Δ v i j 和 Δpij Δ p i j 分别是在非惯性参考系 Bi B i 中物体在 t=tj t = t j 时刻的转动矩阵、速度和位置。其中参考系 Bi B i 是 t=ti t = t i 时刻跟随物体做“自由落体运动的”的坐标系（ Bi B i 参考系相对 W 系速度为 vi v i ，加速度为重力加速）。所以实际积分值可以写为初始状态和预积分值的简单组合：

Rjvjpj=RiΔRij,=RiΔvij+vi+gΔtij,=RiΔpij+pi+viΔtij+12gΔt2ij. R j = R i Δ R i j , v j = R i Δ v i j + v i + g Δ t i j , p j = R i Δ p i j + p i + v i Δ t i j + 1 2 g Δ t i j 2 .

调整初始状态 Ri R i 、 vi v i 和 pi p i 后带入上式即可得到后续状态的积分结果。

预积分中的（高斯）噪声传递

上述公式里虽然将积分与初始值分离，但积分项里仍然存在（未知的）偏移和噪声，对实际计算来说仍然难以使用（或者直接使用后计算结果随时间推移将会出现较大偏差）。实际上通常需要预先标定好惯性器件的偏移（即 bg b g 与 ba b a ）再带入公式计算。

更一般的，在算力允许的情况下可以不直接使用上述公式，而是通过最小化噪声的影响从而估计出 R R 、 v v 、 p p 和 b b 的大小（虽然可以选取不同的最优化模型量化噪声的影响，但所有模型中其大小都将与待测量相关，因此才可以进行最优化估计）。第二个方法可以自然地推广到多种探测器的情形，因此适用于惯性器件与视觉融合的情况，本节也将主要介绍如何预估待测物理量的误差。

已知噪声 ηgdk η k g d 和 ηadk η k a d 满足的分布函数，原则上我们可以直接通过预积分方程数值计算出 R R 、 v v 、 p p 的分布函数，进而得到使得联合概率分布最大时的各物理量的取值。然而随着数据量的积累，上述过程消耗的运算量几何级增加，对于长时间实时定位来说不可能适用。因此根据 Forster et al. 里介绍的方法，我们通过小量展开的方式分离并线性化积分项里噪声的贡献（假设噪声远小于测量信号），再进一步假设噪声满足均值为零的高斯分布，从而得到了计算量较小的最优化算法。

首先将方程重新写为误差函数的形式：

δϕijδvijδpij≐−Log(ΔR~TijRTiRj),≐Δv~ij−RTi(vj−vi−gΔtij),≐Δp~ij−RTi(pj−pi−viΔtij−12gΔt2ij). δ ϕ i j ≐ − L o g ( Δ R ~ i j T R i T R j ) , δ v i j ≐ Δ v ~ i j − R i T ( v j − v i − g Δ t i j ) , δ p i j ≐ Δ p ~ i j − R i T ( p j − p i − v i Δ t i j − 1 2 g Δ t i j 2 ) .

其中 Log(⋅) L o g ( ⋅ ) 函数为 Exp(⋅) E x p ( ⋅ ) 函数的逆运算。上式中等号左边是各物理量的误差函数，右边是物理量和 IMU 测量值的组合。建立一套最优化模型，已知各时刻 IMU 的测量数据，根据等号左边各误差函数满足的概率分布，调节右侧物理量的大小使模型达到最优的解即为我们需要的结果。

上式中 ΔR~ij Δ R ~ i j 、 Δv~ij Δ v ~ i j 和 Δp~ij Δ p ~ i j 是去除噪声后的预积分，定义为：

ΔR~ijΔv~ijΔp~ij≐∏k=ij−1Exp[(ω~k−bgi)Δt],≐∑k=ij−1ΔR~ik(a~k−bai)Δt,≐∑k=ij−1[Δv~ikΔt+12ΔR~ik(a~k−bai)Δt2]. Δ R ~ i j ≐ ∏ k = i j − 1 E x p [ ( ω ~ k − b i g ) Δ t ] , Δ v ~ i j ≐ ∑ k = i j − 1 Δ R ~ i k ( a ~ k − b i a ) Δ t , Δ p ~ i j ≐ ∑ k = i j − 1 [ Δ v ~ i k Δ t + 1 2 Δ R ~ i k ( a ~ k − b i a ) Δ t 2 ] .

其大小只依赖于 IMU 的测量值和偏移量。

误差函数 ηΔij≐[δϕTij,δvTij,δpTij]T η i j Δ ≐ [ δ ϕ i j T , δ v i j T , δ p i j T ] T 为噪声导致的偏差，一阶近似下其为噪声 ηgdk η k g d 、 ηadk η k a d 的线性组合：

δϕijδvijδpij≃∑k=ij−1ΔR~Tk+1,jJkrηgdkΔt,≃∑k=ij−1ΔR~ik[−(a~k−bai)∧δϕik+ηadk]Δt,≃∑k=ij−1[δvikΔt−12ΔR~ik(a~k−bai)∧δϕikΔt2+12ΔR~ikηadkΔt2]. δ ϕ i j ≃ ∑ k = i j − 1 Δ R ~ k + 1 , j T J r k η k g d Δ t , δ v i j ≃ ∑ k = i j − 1 Δ R ~ i k [ − ( a ~ k − b i a ) ∧ δ ϕ i k + η k a d ] Δ t , δ p i j ≃ ∑ k = i j − 1 [ δ v i k Δ t − 1 2 Δ R ~ i k ( a ~ k − b i a ) ∧ δ ϕ i k Δ t 2 + 1 2 Δ R ~ i k η k a d Δ t 2 ] .

已知噪声的统计分布后，可以很容易地使用上式计算出各物理量的误差分布。方程中符号 Jkr≐Jr[(ω~k−bgi)Δt] J r k ≐ J r [ ( ω ~ k − b i g ) Δ t ] ，其中 Jr(ϕ) J r ( ϕ ) 是 SO(3) 群的 right Jacobian，其定义请参见文献 Forster et al. 第三节的介绍。

视觉部分（高斯）噪声传递

本节中视觉定位的误差项主要产生于图像捕捉和匹配过程中的定位误差。考虑到眼镜上搭载的相机为鱼眼式，本节主要推导双目鱼眼相机定位时的误差项 δpci δ p i c 。类似于惯性器件的情况，选定一个最优化模型并输入 δpci δ p i c ，即可得到需要的目标物体的位置信息。

双目相机定位的原理和公式有许多参考资料，因此不介绍了。设左眼相机（C(amera) 系）到世界系（W 系）间的变换为 (RWC,pC) ( R W C , p C ) ，右眼相机相对左眼相机的位姿为 (RLR,pR) ( R L R , p R ) 。一般来说左右眼相机的位姿 (RLR,pR) ( R L R , p R ) 会提前标定好，可以认为其大小固定不变；本节中方便推导假设 RLR=I R L R = I 、 pR=[b,0,0]T p R = [ b , 0 , 0 ] T （即假设右眼相机相对左眼相机只有 x 轴方向的平移且平移量等于 b）。实时定位相机的位姿 (RWC,pC) ( R W C , p C ) 本身即为一个难题（SLAM），本节假设 (RWC,pC) ( R W C , p C ) 已知，所以有：

δpci=RWCηlci. δ p i c = R W C η i l c .

其中 ηlci η i l c 是左眼相机的相机系里物体位置坐标的误差函数，大小等于

(ηlci)x(ηlci)y(ηlci)z=b(x¯′L−x¯′R)2(−x¯′Rη′L+x¯′Lη′R),=b(x¯′L−x¯′R)2y¯′L(−η′L+η′R)+bx¯′L−x¯′Rζ′L,=b(x¯′L−x¯′R)2(−η′L+η′R). ( η i l c ) x = b ( x ¯ L ′ − x ¯ R ′ ) 2 ( − x ¯ R ′ η L ′ + x ¯ L ′ η R ′ ) , ( η i l c ) y = b ( x ¯ L ′ − x ¯ R ′ ) 2 y ¯ L ′ ( − η L ′ + η R ′ ) + b x ¯ L ′ − x ¯ R ′ ζ L ′ , ( η i l c ) z = b ( x ¯ L ′ − x ¯ R ′ ) 2 ( − η L ′ + η R ′ ) .

式中 p′L(R)≐[x¯′L(R)+η′L(R),y¯′L(R)+ζ′L(R),1]T≡[xL(R)/zL(R),yL(R)/zL(R),1]T p L ( R ) ′ ≐ [ x ¯ L ( R ) ′ + η L ( R ) ′ , y ¯ L ( R ) ′ + ζ L ( R ) ′ , 1 ] T ≡ [ x L ( R ) / z L ( R ) , y L ( R ) / z L ( R ) , 1 ] T 是约化的相机系坐标，其中 [xL(R),yL(R),zL(R)]T [ x L ( R ) , y L ( R ) , z L ( R ) ] T 分别是左（右）眼相机参考系中的位置坐标，而 (⋅)¯ ( ⋅ ) ¯ 和 η′ η ′ 、 ζ′ ζ ′ 则指代坐标的均值和误差项。

之后为简化记号因此不再区分左右相机。对鱼眼相机，误差函数满足：

(η′ζ′)=Θ−1(1/fx1/fy)ηt, ( η ′ ζ ′ ) = Θ − 1 ( 1 / f x 1 / f y ) η t ,

其中 ηt η t 是像素平面上物体坐标的测量误差：

pp=(u+ηtv+ηt), p p = ( u + η t v + η t ) ,

fx f x 和 fy f y 是相机的焦距，而矩阵 Θ Θ 为 2×2 2 × 2 矩阵，其中各元素等于

θ11θ12θ21θ22=x¯′2(a+y¯′2x¯′2θdr¯′3),=x¯′y¯′(a−θdr¯′3),=x¯′y¯′(a−θdr¯′3),=y¯′2(a+x¯′2y¯′2θdr¯′3). θ 11 = x ¯ ′ 2 ( a + y ¯ ′ 2 x ¯ ′ 2 θ d r ¯ ′ 3 ) , θ 12 = x ¯ ′ y ¯ ′ ( a − θ d r ¯ ′ 3 ) , θ 21 = x ¯ ′ y ¯ ′ ( a − θ d r ¯ ′ 3 ) , θ 22 = y ¯ ′ 2 ( a + x ¯ ′ 2 y ¯ ′ 2 θ d r ¯ ′ 3 ) .

其中

r¯′θθda=x¯′2+y¯′2−−−−−−−√,=arctan(r¯′)=θ(1+k1θ2+k2θ4+k3θ6+k4θ8),=2θ2(k1+2k2θ2+3k3θ4+4k4θ6)+θd/θr¯′2(1+r¯′2). r ¯ ′ = x ¯ ′ 2 + y ¯ ′ 2 , θ = arctan ⁡ ( r ¯ ′ ) θ d = θ ( 1 + k 1 θ 2 + k 2 θ 4 + k 3 θ 6 + k 4 θ 8 ) , a = 2 θ 2 ( k 1 + 2 k 2 θ 2 + 3 k 3 θ 4 + 4 k 4 θ 6 ) + θ d / θ r ¯ ′ 2 ( 1 + r ¯ ′ 2 ) .

ki k i （ i=1∼4 i = 1 ∼ 4 ）是鱼眼相机的畸变参数。