【多目标优化算法】非支配的精英策略遗传算法:NSGA-II
多目标优化算法,非支配的精英策略遗传算法:NSGA-II
1.算法简介
-
NSGA-II算法特点:快速非支配排序算法、精英保留策略、拥挤度分配策略。
-
相比于NSGA的优势:
-
排序算法的时间复杂度 O ( M N 2 ) O(MN^2) O(MN2)
-
精英保留策略
-
无需要共享的参数
2.算法相关概念
2.1 Pareto optimum
Pareto解又称非支配解或不受支配解(nondominated solutions):在有多个目标时,由于存在目标之间的冲突和无法比较的现象,一个解在某个目标上是最好的,在其他的目标上可能是最差的。这些在改进任何目标函数的同时,必然会削弱至少一个其他目标函数的解称为非支配解或Pareto解。一组目标函数最优解的集合称为Pareto最优集。最优集在空间上形成的曲面称为Pareto前沿面。一组目标函数最优解的集合称为Pareto最优集。
2.2 非支配的快速排序
整个种群的大小为P,首先需要计算出种群中的每个个体的 p p p和被支配个数 n p n_p np和该个体支配解的集合 S p S_p Sp。
- 生成 n p n_p np和 S p S_p Sp的算法过程
for each p ∈ P p\in P p∈P (遍历种群中的每个个体)
S p = ∅ S_p=\emptyset Sp=∅
n p = 0 n_p = 0 np=0
for each q ∈ P q\in P q∈P
if( p < q p < q p<q )then (如果p能支配q)
S p S_p Sp = S p S_p Sp ⋃ \bigcup ⋃ { p } \{p\} {p}(将q加入到被p支配的解集中)
else if( q < p q < p q<p) then
n p = n p + 1 n_p = n_p +1 np=np+1 (增加p的支配数)
if n p = 0 n_p = 0 np=0 then
p r a n k = 1 p_{rank}= 1 prank=1
F 1 = F 1 ⋃ { p } F_1=F_1 \bigcup \{p\} F1=F1⋃{p}
- 排序算法过程
i = 1 i = 1 i=1
while F i ≠ ∅ F_i \neq \emptyset Fi̸=∅
Q = ∅ Q = \emptyset Q=∅ (用来存储下一个的集合)
for each p ∈ F i p \in F_i p∈Fi
for each q ∈ S p q \in S_p q∈Sp (遍历支配解)
n q = n q − 1 n_q = n_q -1 nq=nq−1
if n q = 0 n_q = 0 nq=0 then (q属于下一个集合)
q r a n k = i + 1 q_{rank}= i + 1 qrank=i+1
Q = Q ⋃ { q } Q = Q \bigcup \{q\} Q=Q⋃{q}
i = i + 1 i = i +1 i=i+1
F i = Q F_i = Q Fi=Q
2.3 拥挤度分配
我们引入了拥挤距离KaTeX parse error: Expected '}', got 'EOF' at end of input: I[i]_{distance}$来代替用户定义的共享参数,为了使解在目标空间更加均匀,并且提高了计算复杂度。算法步骤如下:
crowding-distance-assignment( I I I)
-
n u m = ∣ I ∣ . n num = |I|.n num=∣I∣.n,记录 I I I的数量
-
for each i i i, 设 I [ i ] d i s t a n c e = 0 I[i]_{distance}= 0 I[i]distance=0
-
for each objective m m m(对每个目标函数 f m f_m fm):
- 根据目标函数对该种群进行个体排序,其中 f m m a x f_m^{max} fmmax为目标函数 f m f_m fm的最大值, f m m i n f_m^{min} fmmin为最小值
- 排序后的前边界 I [ 1 ] d i s t a n c e I[1]_{distance} I[1]distance和后便捷 I [ n u m ] d i s t a n c e I[num]_{distance} I[num]distance拥挤距离设为 ∞ \infty ∞
- for i = 2 i = 2 i=2 to ( n u m − 1 ) (num - 1) (num−1),计算除边界外所有点 I [ i ] d i s t a n c e = I [ i ] d i s t a n c e + ( f m ( i + 1 ) − f m ( i − 1 ) ) / ( f m m a x − f m m i n ) I[i]_{distance} = I[i]_{distance}+(f_m(i+1)-f_m(i-1))/(f_m^{max}-f_m^{min}) I[i]distance=I[i]distance+(fm(i+1)−fm(i−1))/(fmmax−fmmin)
该拥挤距离度,就是使目标能生成最大的矩阵,且不干扰到其他点。

2.4 精英保留策略
算法步骤如下:
-
将父代种群 P i P_i Pi和子代种群 C i C_i Ci合并成 R i R_i Ri,此时种群数量为 2 N 2N 2N
-
R i R_i Ri根据Pareto进行排序,根据Pareto的等级,将等级最低的优先放入新的父代种群 P i P_i Pi,直到此代放满既定种群数量N
-
在第二步放入排序中,按照拥挤距离从大到小放入到 P i P_i Pi
2.5 锦标赛选择
算法步骤如下:
-
确定每次选择的个体数量 k k k,种群总数为 N N N, k < N k < N k<N
-
从种群中随机选择 k k k个个体(每个个体被选中的概率相同),根据每个个体的适应度,选择适应度值最好的个体进入下一代种群
-
重复步骤(2),直到新的种群规模达到原来的总数 N N N为止
3.算法实现流程图
主体循环部分:
1.随机初始化一个种群 P 0 P_0 P0,对 P 0 P_0 P0进行非支配排序,初始化每个个体的rank值, i = 0 i=0 i=0。
2.通过锦标赛法从 P i P_i Pi选择个体,进行交叉和变异,产生新一代种群 Q i Q_i Qi。
3.将 P i P_i Pi和 Q i Q_i Qi合并,产生一个结合后的种群 R i R_i Ri。
4.对 R i R_i Ri进行非支配排序,并使用拥挤距离和精英保留策略选出每代的N个个体,组成新一代种群 P i + 1 P_{i+1} Pi+1。
5.跳转至2,直至达到预期代数。
4.仿真结果及说明
以下是对ZDT1,ZDT2,ZDT3,ZDT4,ZDT6测试问题的仿真
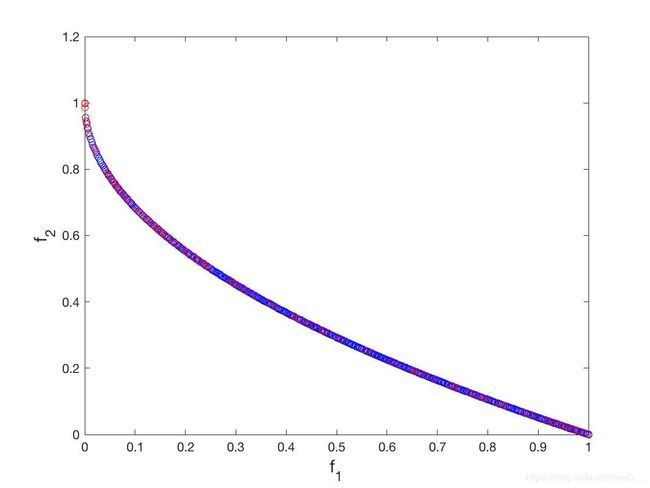
- ZDT1
f 1 ( X ) = x 1 f_1(X) = x_1 f1(X)=x1
f 2 ( X ) = g ( X ) [ 1 − x 1 / g ( X ) ] f_2(X) = g(X)[1-\sqrt{x_1/g(X)}] f2(X)=g(X)[1−x1/g(X)]
g ( X ) = 1 + 9 ( ∑ i = 2 n x i ) / ( n − 1 ) g(X) = 1+9(\sum_{i=2}^nx_i)/(n-1) g(X)=1+9(i=2∑nxi)/(n−1)
n = 30 , n=30, n=30,
x 1 ∈ [ 0 , 1 ] , x i = 0 x_1\in[0,1],x_i = 0 x1∈[0,1],xi=0
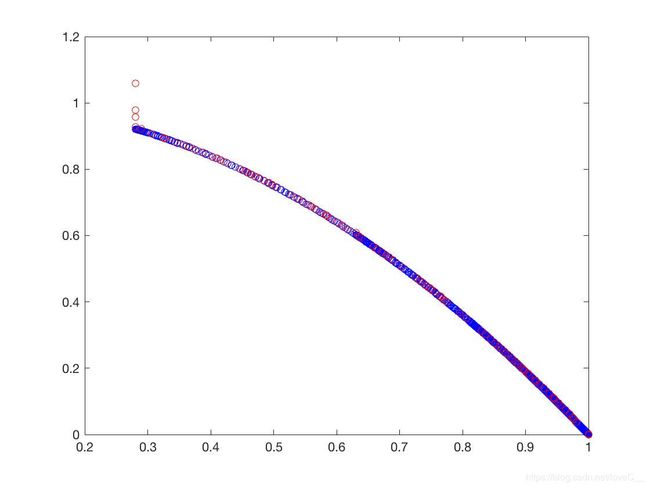
设置初始种群大小为500,迭代次数为500代, p c = 0.9 , p m = 1 / 30 , η c = 20 , η m = 20 p_c = 0.9,p_m=1/30,\eta_c =20,\eta_m=20 pc=0.9,pm=1/30,ηc=20,ηm=20。结果如图(1)所示。

- ZDT2
f 1 ( X ) = x 1 f_1(X) = x_1 f1(X)=x1
f 2 ( X ) = g ( X ) [ 1 − ( x 1 / g ( X ) ) 2 ] f_2(X) = g(X)[1-(x_1/g(X))^2] f2(X)=g(X)[1−(x1/g(X))2]
g ( X ) = 1 + 9 ( ∑ i = 2 n x i ) / ( n − 1 ) g(X) = 1+9(\sum_{i=2}^nx_i)/(n-1) g(X)=1+9(i=2∑nxi)/(n−1)
n = 30 , n=30, n=30,
x 1 ∈ [ 0 , 1 ] , x i = 0 x_1\in[0,1],x_i = 0 x1∈[0,1],xi=0
设置初始种群大小为500,迭代次数为500代, p c = 0.9 , p m = 1 / 30 , η c = 20 , η m = 20 p_c = 0.9,p_m=1/30,\eta_c =20,\eta_m=20 pc=0.9,pm=1/30,ηc=20,ηm=20。结果如图(3)所示。
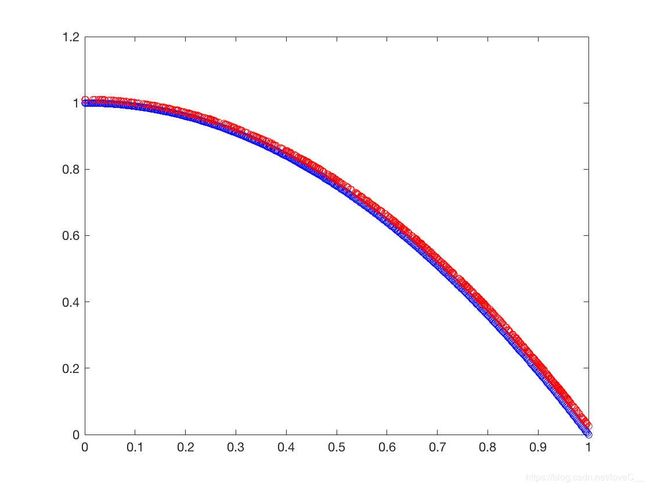
f 1 ( X ) = x 1 f_1(X) = x_1 f1(X)=x1
f 2 ( X ) = g ( X ) [ 1 − x 1 / g ( X ) − x 1 g ( X ) sin ( 10 π x 1 ) ] f_2(X) = g(X)[1-\sqrt{x_1/g(X)}-{\frac{x_1}{g(X)}}\sin(10\pi x_1)] f2(X)=g(X)[1−x1/g(X)−g(X)x1sin(10πx1)]
g ( X ) = 1 + 9 ( ∑ i = 2 n x i ) / ( n − 1 ) g(X) = 1+9(\sum_{i=2}^nx_i)/(n-1) g(X)=1+9(i=2∑nxi)/(n−1)
n = 30 , n=30, n=30,
x 1 ∈ [ 0 , 1 ] , x i = 0 x_1\in[0,1],x_i = 0 x1∈[0,1],xi=0
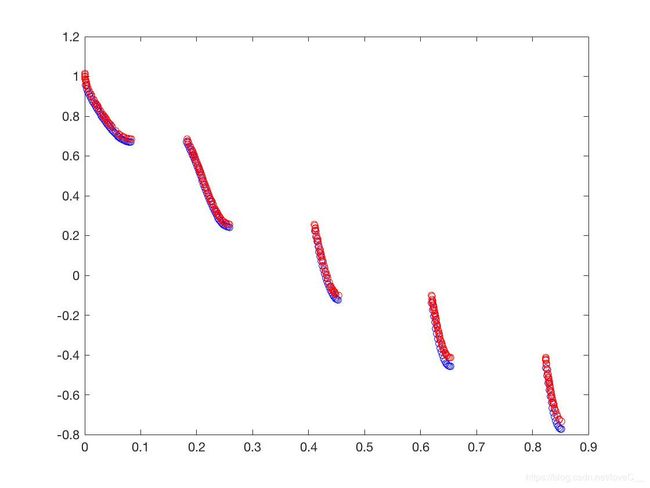
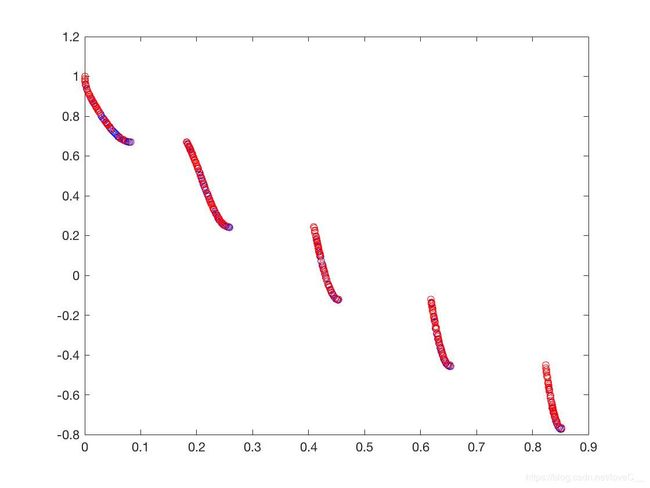
设置初始种群大小为250,迭代次数为500代, p c = 0.9 , p m = 1 / 30 , η c = 20 , η m = 20 p_c = 0.9,p_m=1/30,\eta_c =20,\eta_m=20 pc=0.9,pm=1/30,ηc=20,ηm=20。结果如图(5)所示。
f 1 ( X ) = x 1 f_1(X) = x_1 f1(X)=x1
f 2 ( X ) = g ( X ) [ 1 − x 1 / g ( X ) ] f_2(X) = g(X)[1-\sqrt{x_1/g(X)}] f2(X)=g(X)[1−x1/g(X)]
g ( X ) = 1 + 10 ( n − 1 ) + ∑ n i = 2 [ x i 2 − 10 cos ( 4 π x i ) ] g(X) = 1+10(n-1)+\sum_n^i=2[x_i^2-10\cos(4\pi x_i)] g(X)=1+10(n−1)+n∑i=2[xi2−10cos(4πxi)]
n = 10 , n=10, n=10,
x 1 ∈ [ 0 , 1 ] , x i = 0 x_1\in[0,1],x_i = 0 x1∈[0,1],xi=0
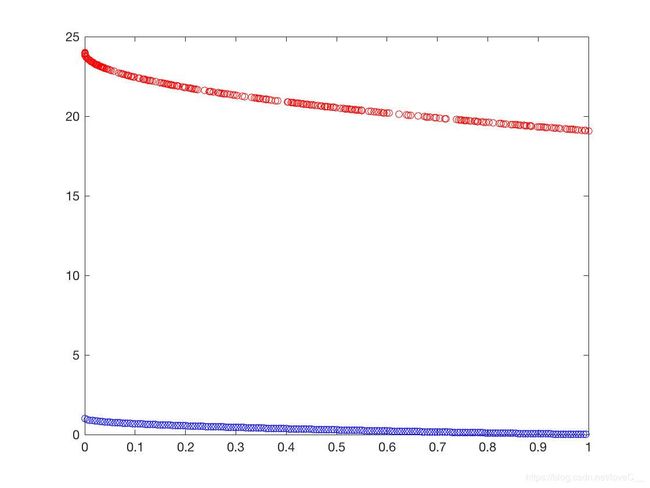
设置初始种群大小为250,迭代次数为500代, p c = 0.9 , p m = 1 / 10 , η c = 20 , η m = 20 p_c = 0.9,p_m=1/10,\eta_c =20,\eta_m=20 pc=0.9,pm=1/10,ηc=20,ηm=20。结果如图(7)所示。
f 1 ( X ) = 1 − e x p ( − 4 π x 1 ) sin 6 ( 6 π x i ) f_1(X)= 1-exp(-4\pi x_1)\sin^6(6\pi x_i) f1(X)=1−exp(−4πx1)sin6(6πxi)
f 2 ( X ) = g ( X ) [ 1 − ( f 1 ( X ) / g ( X ) ) 2 ] f_2(X)= g(X)[1-(f_1(X)/g(X))^2] f2(X)=g(X)[1−(f1(X)/g(X))2]
g ( X ) = 1 + 9 [ ( ∑ n i = 2 x i ) / ( n − 1 ) ] 0.25 g(X) = 1+9[(\sum_n^{i=2}x_i)/(n-1)]^{0.25} g(X)=1+9[(n∑i=2xi)/(n−1)]0.25
n = 10 , n=10, n=10,
x 1 ∈ [ 0 , 1 ] , x i = 0 x_1\in[0,1],x_i = 0 x1∈[0,1],xi=0
设置初始种群大小为100,迭代次数为500代, p c = 0.9 , p m = 1 / 10 , η c = 20 , η m = 20 p_c = 0.9,p_m=1/10,\eta_c =20,\eta_m=20 pc=0.9,pm=1/10,ηc=20,ηm=20。结果如图(9)所示。
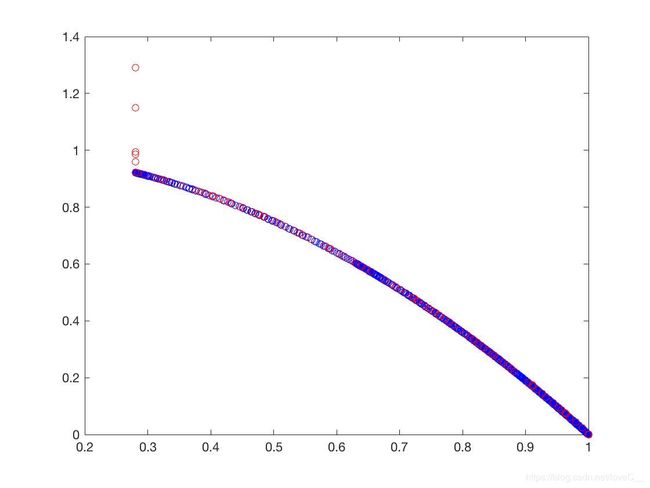
设置初始种群大小为100,迭代次数为500代, p c = 0.9 , p m = 1 / 10 , η c = 20 , η m = 20 p_c = 0.9,p_m=1/10,\eta_c =20,\eta_m=20 pc=0.9,pm=1/10,ηc=20,ηm=20。结果如图(10)所示。
从仿真结果可以得到NSGA-II在测试问题ZDT1、ZDT2、ZDT3甚至是ZDT6都呈现出了不错的结果,非常接近Pareto-front值,只有在ZDT4问题上表现较差。
Δ \Delta Δ的Mean和Vairance
| Problem | ZDT1 | ZDT2 | ZDT3 | ZDT4 | ZDT6 |
|---|---|---|---|---|---|
| Mean(500) | 0.4569 | 0.4583 | 0.6731 | 0.4972 | 0.6956 |
| Vairance(500) | 0.0010 | 0.0317 | 0.0052 | 0.0083 | 0.0041 |
| Mean(2000) | 0.4954 | 0.4890 | 0.6925 | 0.4977 | 0.4544 |
| Vairance(2000) | 0.0056 | 0.0013 | 0.0013 | 0.0057 | 0.0031 |
γ \gamma γ的Mean和Vairance
| Problem | ZDT1 | ZDT2 | ZDT3 | ZDT4 | ZDT6 |
|---|---|---|---|---|---|
| Mean(500) | 0.0118 | 0.1000 | 0.9240 | 22.4199 | 0.5100 |
| Vairance(500) | 0.0082 | 0.0033 | 0.0042 | 0.5061 | 0.0380 |
| Mean(2000) | 0.0013 | 0.0011 | 0.0900 | 16.7371 | 0.4400 |
| Vairance(2000) | 0.0001 | 0.0005 | 0.0003 | 0.4937 | 0.0032 |
根据图(1)和图(2),图(3)与图(4),图(5)与图(6)的对比可以发现,迭代的代数是对最优解结果有一定的影响的,能得到更好的接近Pareto最优值。由图(7)与图(8)可以的看出迭代次数对ZDT6的影响不大。在数据表中 γ \gamma γ数据可以得出,在ZDT4问题上效果较差,从 Δ \Delta Δ数据可以看出,以上5个问题的传播多样性较好。