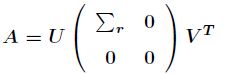几种矩阵分解算法： LU分解，Cholesky分解，QR分解，SVD分解，Jordan分解

目录

1.LU分解

2. LDLT分解法

3. Cholesky分解的形式

4. QR分解

5.SVD分解

5.1 SVD与广义逆矩阵

6. Jordan 分解

参考文章：

---

                                                                                                                                                        ---------我只是搬运工，汇总在此

1.LU分解

       假定我们能把矩阵A写成下列两个矩阵相乘的形式：A=LU，其中L为下三角矩阵，U为上三角矩阵。这样我们可以把线性方程组Ax= b写成

      Ax= (LU)x = L(Ux) = b。令Ux = y，则原线性方程组Ax = b可首先求解向量y 使Ly = b，然后求解 Ux = y，从而达到求解线性方程组Ax= b的目的。

 

2. LDLT分解法

实际问题中，当求解方程组的系数矩阵是对称矩阵时，则用下面介绍的LDLT分解法可以简化程序设计并减少计算量。

从定理可知，当矩阵A的各阶顺序主子式不为零时，A有唯一的Doolittle分解A= LU。矩阵U的对角线元素Uii 不等于0，将矩阵U的每行依次提出，

定理：若对称矩阵A的各阶顺序主子式不为零时，则A可以唯一分解为A= LDLT，这里

LT为L的转置矩阵。

当A有LDLT分解时，利用矩阵运算法则及相等原理易得计算ljk和dk的公式为

3. Cholesky分解

 

Cholesky分解是一种分解矩阵的方法, 在线形代数中有重要的应用。Cholesky分解把矩阵分解为一个下三角矩阵以及它的共轭转置矩阵的乘积（那实数界来类比的话，此分解就好像求平方根）。与一般的矩阵分解求解方程的方法比较，Cholesky分解效率很高。

Cholesky分解的条件

一、Hermitianmatrix：矩阵中的元素共轭对称（复数域的定义，类比于实数对称矩阵）。Hermitiank意味着对于任意向量x和y，(x*)Ay共轭相等

二、Positive-definite：正定（矩阵域，类比于正实数的一种定义）。正定矩阵A意味着，对于任何向量x，(x^T)Ax总是大于零(复数域是(x*)Ax>0)

Cholesky分解的形式

可记作A = L L*。其中L是下三角矩阵。L*是L的共轭转置矩阵。

可以证明，只要A满足以上两个条件，L是唯一确定的，而且L的对角元素肯定是正数。反过来也对，即存在L把A分解的话，A满足以上两个条件。

•     Hermitianmatrix：矩阵中的元素共轭对称（复数域的定义，类比于实数对称矩阵）。Hermitiank意味着对于任意向量x和y，(x*)Ay共轭相等
•    Positive-definite：正定（矩阵域，类比于正实数的一种定义）。正定矩阵A意味着，对于任何向量x，(x^T)Ax总是大于零(复数域是(x*)Ax>0)

如果A是半正定的（semi-definite），也可以分解，不过这时候L就不唯一了。

特别的，如果A是实数对称矩阵，那么L的元素肯定也是实数。

另外，满足以上两个条件意味着A矩阵的特征值都为正实数，因为Ax = lamda * x,

(x*)Ax = lamda * (x*)x > 0, lamda > 0

4. QR分解

• 矩阵的QR分解是指，可以将矩阵A分级成一个正交阵Q和一个上三角矩阵R的乘积。实际中，QR分解经常被用来解线性最小二乘问题

。

• 对于非方阵的m∗n(m≥n)m∗n(m≥n)阶矩阵A也可能存在QR分解。这时Q为m*m阶的正交矩阵，R为m*n阶上三角矩阵。这时的QR分解不是完整的(方阵)，因此称为约化QR分解(对于列满秩矩阵A必存在约化QR分解)。同时也可以通过扩充矩阵A为方阵或者对矩阵R补零，可以得到完全QR分解。

5.SVD分解

 对任意矩阵，都能被奇异值分解为

   

   其中是的正交矩阵，是的正交矩阵，是由个沿对角线从大到小排列的奇异值

   组成的方阵，就是矩阵的秩。奇异值分解是一种正交矩阵分解法。

    更多解释参考4.

   SVD分解常用在信息压缩，以及求广义逆：

5.1 SVD与广义逆矩阵

       在认识矩阵的广义逆之前，先来回顾一下方阵的逆。

       对于一个的方阵，如果存在一个矩阵，使得，那么方阵的逆为。

       那么对于非方阵来说情况又是怎样的？ 比如对于的矩阵，它的逆是怎样计算的？这就是我将要    讨论的广义逆矩阵。   矩阵的广义逆由Moore在1920年提出，后来在1955年经过Penrose发展得到如下定义    对任意复数矩阵，如果存在的矩阵，满足

   

   则称为的一个Moore-Penrose逆，简称广义逆，记为。并把上面四个方程叫做Moore-Penrose    方程，简称M-P方程。 

   由于M-P的四个方程都各有一定的解释，并且应用起来各有方便之处，所以出于不同的目的，常常考虑满足

   部分方程的，叫做弱逆，弱逆不唯一。为了引用方便，下面给出广义逆矩阵的定义

   对于的矩阵，若存在的矩阵，满足M-P方程中的全部或者其中的一部分，则称为

   的广义逆矩阵。

   实际上有结论：如果满足M-P方程中的全部四个条件，那么得到的矩阵是唯一的，如果只满足部分条件，

   那么得到的矩阵不唯一。也就是说一个矩阵的Moore-Penrose逆是唯一的。

   而广义逆的计算可以利用的SVD分解得到，假设矩阵的SVD分解为

   

   那么，不难验证

   

   有了广义逆矩阵，那么就可以用来求解线性方程组，假设现在已经知道了矩阵的广义逆，

   如果矩阵的秩是，则其唯一解是，如果秩小于，则有无穷多组解，其中最小范数解仍然是

   ，通常我们关心的也就是这个解。

 

6. Jordan 分解

 

但运行速度从快到慢为： 
LU分解 > Qr分解 > 求逆

参考文章：

1. https://blog.csdn.net/zhouliyang1990/article/details/21952485
2. https://blog.csdn.net/qq_30981697/article/details/71545519
3. https://blog.csdn.net/renhaofan/article/details/80740697
4. https://blog.csdn.net/billbliss/article/details/78579308
5. https://blog.csdn.net/xuehuafeiwu123/article/details/53321730