视觉slam14讲——第8讲 视觉里程计2
本系列文章是记录学习高翔所著《视觉slam14讲》的内容总结，文中的主要文字和代码、图片都是引用自课本和高翔博士的博客。代码运行效果是在自己电脑上实际运行得出。手动记录主要是为了深入理解
- 直接法简介
- 1 特征点法的缺点
- 2 克服这些缺点的思路
- 3 特征点法和直接法区别
- 光流法
- 1 LK光流
- 直接法Direct Method
- 1 简介推导
- 2 直接法分类
- 3 直接法的讨论
- 4 直接法的优缺点总结
- 代码实践
- 1 LK光流
- 2 RGB-D直接法
- 21 稀疏直接法
- 22 半稠密直接法
相比于特征点法，主要是介绍了视觉里程计的另一个分支——直接法。
1 直接法简介
1.1 特征点法的缺点
- 关键点的提取和描述子计算非常耗时
- 使用特征点忽略了除特征点以外的其他信息
- 相机可能运动到特征点缺失的地方，这些地方没有明显的纹理信息
1.2 克服这些缺点的思路
- 提取特征点，但是只计算关键点，不计算描述子，使用光流法（Optical Flow）
这种方法仍然使用特征点，只是把匹配描述子替换成光流跟踪，估计相机运动仍然使用对极几何、PnP或者ICP算法 - 提取特征点，但是只计算关键点，不计算描述子，使用直接法（Direct Method）
- 不使用特征点，根据像素灰度差异，直接计算相机运动
后两种方法称为直接法
1.3 特征点法和直接法区别
- 特征点法：最小化重投影误差（Reprojection Error）优化相机运动，需要精确地知道空间点在两个相机中投影后的像素位置，这也是需要匹配跟踪的原因，但是计算量大。
- 直接法：不需要知道点和点的匹配关系，通过最小化光度误差（Photometric Error）
2 光流法
直接法是从光流法演变而来，他们具有相同的假设条件。光流是描述像素随时间在图像之间运动的方法。
- 计算部分像素运动的稀疏光流
- 计算所有像素运动的稠密光流
主要介绍Lucas-Kanade光流，成为LK光流。
2.1 LK光流
灰度不变假设：同一空间点的像素灰度值在各个图像中是固定不变的。
I(x+dx,y+dy,t+dt)=I(x,y,t)
对左边进行泰勒一阶展开，两边同时除以 dt 。
记 Ix，Iy 是图像梯度， u,v 是像素运动速度， It 是图像灰度时间变化。写成矩阵形式
[IxIy][uv]=−It
考虑一个大小 ω∗ω 窗口，含有 ω2 个像素，得到 ω2 个方程。
[IxIy]k[uv]=−Itk,k=1,2,...,ω2
记作$\begin{bmatrix}
I_x & I_y
\end{bmatrix} k 系列方程矩阵为 A ， I{tk} 系列方程矩阵为 b$,
A[uv]=−b
传统解法是求最小二乘解，
[uv]∗=−(ATA)−1ATb
3 直接法（Direct Method）
3.1 简介推导
投影方程如下
p1=[uv]1=D1Z1KP
p2=[uv]2=D1Z2K(RP+t)=D1Z2Kexp(ξ∧)P
在直接法中，是求解一个优化问题，但这个优化最小化的不是重投影误差，而是测量误差（Photometric Error），也就是 P的两个像的亮度误差
e=I1(p1)−I2(p2)
优化该误差的目标函数
minξJ(ξ)=eTe
3.2 直接法分类
在上面的推导中，P是一个已知位置的空间点，在RGB-D相机下，我们可以把任意像素反投影到三维空间，然后投影到下一个图像中。如果在单目相机中，可以使用已经估计好位置的特征点（虽然是特征点，但直接法里是可以避免计算描述子的）。根据P的来源，把直接法进行分类：
- P来自于稀疏特征点，称之为稀疏直接法。通常我们使用数百个特征点，并且会像L-K光流那样，假设它周围像素也是不变的。这种稀疏直接法速度不必计算描述子，并且只使用数百个像素，因此速度最快，但只能计算稀疏的重构。
- P来自部分像素, 这称之为半稠密（Semi-Dense）的直接法，考虑只使用带有梯度的像素点，舍弃像素梯度不明显的地方，可以重构一个半稠密结构。
- P为所有像素，称为稠密直接法。稠密重构需要计算所有像素（一般几十万至几百万个），因此多数不能在现有的 CPU上实时计算，需要GPU的加速。
可以看到，从稀疏到稠密重构，都可以用直接法来计算。它们的计算量是逐渐增长的。稀疏方法可以快速地求解相机位姿，而稠密方法可以建立完整地图。
3.3 直接法的讨论
比于特征点法，直接法完全依靠像优化来求解相机位姿，像素梯度引导着优化的方向。如果想要得到正确的优化结果，就必须保证大部分像素梯度能够把优化引导到正确的方向。
一次迭代的图像化演示
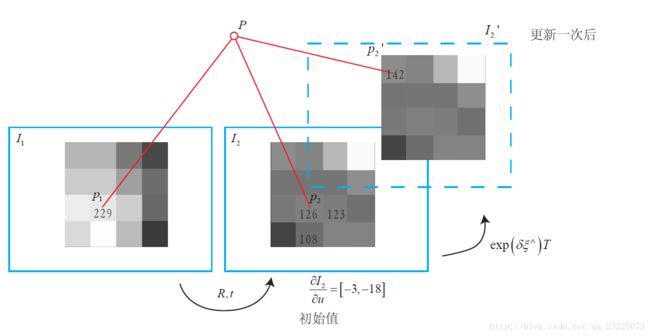
如何知道往哪里微调像素会更亮呢？这就需要用到像素梯度。
直接法的梯度是直接由图像梯度确定的，因此我们必须保证沿着图像梯度走时，灰度误差会不断下降。然而，图像通常是一个很强烈的非凸函数，如下图所示。实际当中，如果我们沿着图像梯度前进，很容易由于图像本身的非凸性（或噪声）落进一个局部极小值中，无法继续优化。只有当相机运动很小，图像中的梯度不会有很强的非凸性时，直接法才能成立。
3.4 直接法的优缺点总结
最后，我们总结一下直接法的优缺点。大体来说，它的优点如下：
- 可以省去计算特征点、描述子的时间。
- 只要求有像素梯度即可，无须特征点。因此，直接法可以在特征缺失的场合下使用。
- 可以构建半稠密乃至稠密的地图，这是特征点法无法做到的。
另一方面，它的缺点也很明显：
- 非凸性。直接法完全依靠梯度搜索，降低目标函数来计算相机位姿。其目标函数中需要取像素点的灰度值，而图像是强烈非凸的函数。这使得优化算法容易进入极小，只在运动很小时直接法才能成功。
- 单个像素没有区分度。找一个和他像的实在太多了！——于是我们要么计算图像块，要么计算复杂的相关性。由于每个像素对改变相机运动的“意见”不一致。只能少数服从多数，以数量代替质量。
- 灰度值不变是很强的假设。如果相机是自动曝光的，当它调整曝光参数时，会使得图像整体变亮或变暗。光照变化时亦会出现这种情况。特征点法对光照具有一定的容忍性，而直接法由于计算灰度间的差异，整体灰度变化会破坏灰度不变假设，使算法失败。
4 代码实践
4.1 LK光流
#include
#include return 1;
}
string path_to_dataset = argv[1];
string associate_file = path_to_dataset + "/associate.txt";
ifstream fin( associate_file );
if ( !fin )
{
cerr<<"I cann't find associate.txt!"<return 1;
}
string rgb_file, depth_file, time_rgb, time_depth;
list< cv::Point2f > keypoints; // 因为要删除跟踪失败的点，使用list
cv::Mat color, depth, last_color;
for ( int index=0; index<100; index++ )
{
fin>>time_rgb>>rgb_file>>time_depth>>depth_file;
color = cv::imread( path_to_dataset+"/"+rgb_file );
depth = cv::imread( path_to_dataset+"/"+depth_file, -1 );
if (index ==0 )
{
// 对第一帧提取FAST特征点
vector detector = cv::FastFeatureDetector::create();
detector->detect( color, kps );
for ( auto kp:kps )
keypoints.push_back( kp.pt );
last_color = color;
continue;
}
if ( color.data==nullptr || depth.data==nullptr )
continue;
// 对其他帧用LK跟踪特征点
vectordouble>>( t2-t1 );
cout<<"LK Flow use time："<" seconds."<// 把跟丢的点删掉
int i=0;
for ( auto iter=keypoints.begin(); iter!=keypoints.end(); i++)
{
if ( status[i] == 0 )
{
iter = keypoints.erase(iter);
continue;
}
*iter = next_keypoints[i];
iter++;
}
cout<<"tracked keypoints: "<if (keypoints.size() == 0)
{
cout<<"all keypoints are lost."<break;
}
// 画出 keypoints
cv::Mat img_show = color.clone();
for ( auto kp:keypoints )
cv::circle(img_show, kp, 10, cv::Scalar(0, 240, 0), 1);
cv::imshow("corners", img_show);
cv::waitKey(0);
last_color = color;
}
return 0;
} 
4.2 RGB-D直接法
4.2.1 稀疏直接法
class EdgeSE3ProjectDirect: public BaseUnaryEdge< 1, double, VertexSE3Expmap>
{
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
EdgeSE3ProjectDirect() {}
EdgeSE3ProjectDirect ( Eigen::Vector3d point, float fx, float fy, float cx, float cy, cv::Mat* image )
: x_world_ ( point ), fx_ ( fx ), fy_ ( fy ), cx_ ( cx ), cy_ ( cy ), image_ ( image )
{}
virtual void computeError()
{
const VertexSE3Expmap* v =static_cast<const VertexSE3Expmap*> ( _vertices[0] );
Eigen::Vector3d x_local = v->estimate().map ( x_world_ );
float x = x_local[0]*fx_/x_local[2] + cx_;
float y = x_local[1]*fy_/x_local[2] + cy_;
// check x,y is in the image
if ( x-4<0 || ( x+4 ) >image_->cols || ( y-4 ) <0 || ( y+4 ) >image_->rows )
{
_error ( 0,0 ) = 0.0;
this->setLevel ( 1 );
}
else
{
_error ( 0,0 ) = getPixelValue ( x,y ) - _measurement;
}
}
// plus in manifold
virtual void linearizeOplus( )
{
if ( level() == 1 )
{
_jacobianOplusXi = Eigen::Matrix<double, 1, 6>::Zero();
return;
}
VertexSE3Expmap* vtx = static_cast ( _vertices[0] );
Eigen::Vector3d xyz_trans = vtx->estimate().map ( x_world_ ); // q in book
double x = xyz_trans[0];
double y = xyz_trans[1];
double invz = 1.0/xyz_trans[2];
double invz_2 = invz*invz;
float u = x*fx_*invz + cx_;
float v = y*fy_*invz + cy_;
// jacobian from se3 to u,v
// NOTE that in g2o the Lie algebra is (\omega, \epsilon), where \omega is so(3) and \epsilon the translation
Eigen::Matrix<double, 2, 6> jacobian_uv_ksai;
jacobian_uv_ksai ( 0,0 ) = - x*y*invz_2 *fx_;
jacobian_uv_ksai ( 0,1 ) = ( 1+ ( x*x*invz_2 ) ) *fx_;
jacobian_uv_ksai ( 0,2 ) = - y*invz *fx_;
jacobian_uv_ksai ( 0,3 ) = invz *fx_;
jacobian_uv_ksai ( 0,4 ) = 0;
jacobian_uv_ksai ( 0,5 ) = -x*invz_2 *fx_;
jacobian_uv_ksai ( 1,0 ) = - ( 1+y*y*invz_2 ) *fy_;
jacobian_uv_ksai ( 1,1 ) = x*y*invz_2 *fy_;
jacobian_uv_ksai ( 1,2 ) = x*invz *fy_;
jacobian_uv_ksai ( 1,3 ) = 0;
jacobian_uv_ksai ( 1,4 ) = invz *fy_;
jacobian_uv_ksai ( 1,5 ) = -y*invz_2 *fy_;
Eigen::Matrix<double, 1, 2> jacobian_pixel_uv;
jacobian_pixel_uv ( 0,0 ) = ( getPixelValue ( u+1,v )-getPixelValue ( u-1,v ) ) /2;
jacobian_pixel_uv ( 0,1 ) = ( getPixelValue ( u,v+1 )-getPixelValue ( u,v-1 ) ) /2;
_jacobianOplusXi = jacobian_pixel_uv*jacobian_uv_ksai;
}
// dummy read and write functions because we don't care...
virtual bool read ( std::istream& in ) {}
virtual bool write ( std::ostream& out ) const {}
protected:
// get a gray scale value from reference image (bilinear interpolated)
inline float getPixelValue ( float x, float y )
{
uchar* data = & image_->data[ int ( y ) * image_->step + int ( x ) ];
float xx = x - floor ( x );
float yy = y - floor ( y );
return float (
( 1-xx ) * ( 1-yy ) * data[0] +
xx* ( 1-yy ) * data[1] +
( 1-xx ) *yy*data[ image_->step ] +
xx*yy*data[image_->step+1]
);
}
public:
Eigen::Vector3d x_world_; // 3D point in world frame
float cx_=0, cy_=0, fx_=0, fy_=0; // Camera intrinsics
cv::Mat* image_=nullptr; // reference image
}; 
4.2.2 半稠密直接法
// select the pixels with high gradiants
for ( int x=10; x10; x++ )
for ( int y=10; y10; y++ )
{
Eigen::Vector2d delta (
gray.ptr<uchar>(y)[x+1] - gray.ptr<uchar>(y)[x-1],
gray.ptr<uchar>(y+1)[x] - gray.ptr<uchar>(y-1)[x]
);
if ( delta.norm() < 50 )
continue;
ushort d = depth.ptr<ushort> (y)[x];
if ( d==0 )
continue;
Eigen::Vector3d p3d = project2Dto3D ( x, y, d, fx, fy, cx, cy, depth_scale );
float grayscale = float ( gray.ptr<uchar> (y) [x] );
measurements.push_back ( Measurement ( p3d, grayscale ) );
} 