【Gym 102134-E】Kth subtree【权值树状数组、二分统计第k大+dfs离线操作】

题意：

给出一棵 $n$ 个点的树，一共有 $q$ 组询问，每次询问给出$v$、$k$，表示将点 $v$ 当做根节点之后，所有节点中子树大小的第 $k$ 大是多少。$(1\le n\le 10^5,1\le q\le 10^5)$

---

思路：

首先需要观察的是换根之后，哪些节点的子树大小会发生改变。稍微模拟一下就会发现，如果新根为 $y$，则只有从 $root$ 到 $y$ 这条路径上的点的子树大小会发生变化。假设节点$y$的父节点为$now$，则节点$now$子树大小变化为 $n-siz[y]$。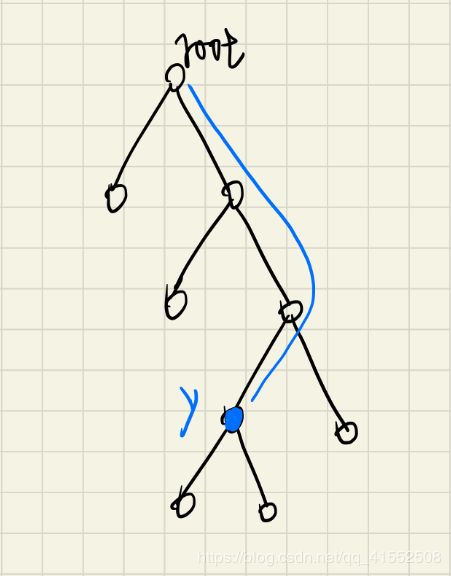
因此我们考虑离线操作，先记录哪些节点会成为新根，并且记录这些节点成为新根之后需要统计的$k$。然后从上往下进行$dfs$时，将经过的节点的子树大小进行改变，然后统计当前状态下的第$k$大数。对于这步操作我们可以使用权值树状数组+二分来进行统计，然后求出答案即可。

---

总结：

这题主要收获在于在线转离线，并且练习了权值树状数组+二分代替了权值线段树。

---

代码：

#include 
#include 
#include 
#include 
#include 
#include 
#define LOG1(x1,x2) cout << x1 << ": " << x2 << endl;
#define LOG2(x1,x2,y1,y2) cout << x1 << ": " << x2 << " , " << y1 << ": " << y2 << endl;
#define LOG3(x1,x2,y1,y2,z1,z2) cout << x1 << ": " << x2 << " , " << y1 << ": " << y2 << " , " << z1 << ": " << z2 << endl;
#define rep(i,a,b) for(int i = a; i <= b; i++)
using namespace std;
const int N = 1e5+10;
const int M = 1e5+10;
 
int t[N];
int n,q,tot,head[N],sz,flag[N];
struct Edge{
	int to,next;
}e[2*M];
int query[N][2],siz[N];
vector<int> vis[N],mp[N];
void add(int x,int y){
	e[++tot].to = y, e[tot].next = head[x], head[x] = tot;
}

inline int lowbit(int x) { return x&(-x); }
inline void update(int x,int cc) { while(x <= n) t[x] += cc, x += lowbit(x); }
inline int ask(int x){ int tp = 0; while(x) tp += t[x], x -= lowbit(x); return tp;}
 
int dfs(int x,int fa){
	int cc = 0;
	if(vis[x].size() >= 1) cc = 1; //求出节点siz[x]
	siz[x] = 1;
	for(int i = head[x]; i; i = e[i].next){
		int y = e[i].to;
		if(y == fa) continue;
		if(dfs(y,x)) cc = 1;
		siz[x] += siz[y];
	}
	flag[x] = cc;
	return cc;
}	

int find(int kk){
	int l = 1, r = n, ans = 1e6;
	while(l <= r){
		int mid = (l+r)>>1;
		int numm = ask(mid);
		if(numm >= kk) r = mid-1, ans = min(ans,mid);
		else if(numm < kk) l = mid+1;
	}
	return ans;
}

void dfs_ans(int x,int fa){
	if(!flag[x]) return;
	update(siz[x],-1);
	for(int i = head[x]; i; i = e[i].next){
		int y = e[i].to;
		if(y == fa) continue;
		update(n-siz[y],1);
		dfs_ans(y,x);
		update(n-siz[y],-1);
	}
	update(n,1);
	if(vis[x].size()){
		for(int j = 0; j < vis[x].size(); j++){
			int y = find(vis[x][j]); //找第k大
			mp[x].push_back(y); //mp存答案
		}
	}
	update(n,-1); //消除影响
	update(siz[x],1); //恢复原来状态
}

int main()
{
	scanf("%d%d",&n,&q);
	rep(i,1,n-1){
		int x,y; scanf("%d%d",&x,&y);
		add(x,y); add(y,x);
	}
	rep(i,1,q){
		int x,y; scanf("%d%d",&x,&y);
		query[i][0] = x;
		vis[x].push_back(y);
		query[i][1] = vis[x].size()-1;
	}
	dfs(1,-1);
	rep(i,1,n) update(siz[i],1); //插入初始值
	dfs_ans(1,-1);
	rep(i,1,q){
		int x = query[i][0], y = query[i][1];
		printf("%d\n",mp[x][y]);
	}
	return 0;
}