Java二叉树笔试题总结
1、前序遍历,中序遍历,后序遍历;层次遍历;
2、求树的结点数;
3、求树的叶子数;
4、求树的深度;
5、求二叉树第 k 层的结点个数;
6、判断两棵二叉树是否结构相同;
7、求二叉树的镜像;
8、求两个结点的最低公共祖先结点;
9、求任意两结点距离;
10、找出二叉树中某个结点的所有祖先结点;
11、不使用递归和栈遍历二叉树;
12、二叉树前序中序推后序;
13、判断二叉树是不是完全二叉树;
14、判断是否是二叉查找树的后序遍历结果;
15、给定一个二叉查找树中的结点,找出在中序遍历下它的后继和前驱;
16、二分查找树转化为排序的循环双链表;
17、有序链表转化为平衡的二分查找树;
18、判断是否是二叉查找树。
0、创建一棵二叉树
public class TreeNode {
int val = 0;
TreeNode left = null;
TreeNode right = null;
public TreeNode(int val) {
this.val = val;
}
1.1、前序遍历(中、左、右)
(a)递归版本
public void preOrder(TreeNode root){
if(null!=root){
System.out.print(root.val+"\t");
preOrder(root.left);
preOrder(root.right);
}
}
(b)非递归:借用一个栈来实现
前序,中序,后序遍历,不管是递归版本还是非递归版本,都用到了一个数据结构 – 栈,为何要用栈?那是因为其它的方式没法记录当前结点的 parent。
public void preOrder(TreeNode root){
Stack stack=new Stack();
while(true){
while(root != null){
System.out.print(root.val+"\t");
stack.push(root);
root=root.left;
}
//退出循环说明左子树已经全部输出了
if(stack.isEmpty()) break;
root=stack.pop();
//开始输出右子树
root=root.right;
}
}
1.2、中序遍历(左、中、右)
(a)、递归
public void inOrder(TreeNode root){
if(null != root){
inOrder(root.left);//先递归到二叉树的最左子节点
System.out.print(root.val+"\t");
inOrder(root.right);
}
}
(b)、非递归:借用栈实现
public void inOrder(reeNode root){
Stack stack=new Stack();
while(true){
while(root != null){
stack.push(root);
root=root.left;
}//递归到最左子节点
if(stack.isEmpty())break;
root=stack.pop();
System.out.print(root.val+"\t");
root=root.right;
}
}
}
1.3、后序遍历(左、右、中)
(a)、递归
public void postOrder(TreeNode root){
if(root != null){
postOrder(root.left);
postOrder(root.right);
System.out.print(root.val+"\t");
}
}
(b)、非递归
public void postOrder(TreeNode root){
Stack stack=new Stack();
while(true){
if(root != null){
stack.push(root);
root=root.left;
}else{
if(stack.isEmpty()) return;
if(null==stack.lastElement().right){
root=stack.pop();
System.out.print(root.val+"\t");
while(root==stack.lastElement().right){
System.out.print(stack.lastElement().val+"\t");
root=stack.pop();
if(stack.isEmpty()){
break;
}
}
}
if(!stack.isEmpty())
root=stack.lastElement().right;
else
root=null;
}
}
}
1.4、层序遍历:借助一个队列
public List Cengxu(TreeNode root){
List res = new ArrayList();
LinkedList queue = new LinkedList();
if (root == null){
return res;
}
queue.offer(root);
while( !queue.isEmpty() ){
TreeNode temp = queue.poll();
res.add(temp.val);
if (root.left != null){
queue.offer(root.left);
}
if (root.right != null){
queue.offer(root.right);
}
}
return res;
}
2、求树的结点数
public int countNodes(TreeNode root){
if (root == null){
return 0;
}
return countNodes(root.left) +countNodes(root.right) + 1;
}
3、求树的叶子数
叶子结点是二叉树中那些左孩子和右孩子均不存在的结点
public int countLeaves(TreeNode root){
if (root == null){
return 0;
}
if (root.left == null && root.right == null){
return 1;
}
return countLeaves(root.left) + countLeaves(root.right);
}
4、求树的深度
public int Depth(TreeNode root){
if (k==0 || root == null){
return 0;
}
int left = Depth(root.left);
int right = Depth(root.right);
return left > right ? left +1 : right +1;
}
5、求二叉树第k层的节点个数
public int getKNodes(TreeNode root,int k){
if (root == null){
return 0;
}
if (k == 1){
return 1;
}
int leftNum = getKNodes(root.left,k-1);//左子树中K-1层的节点个数
int rightNum = getKNodes(root.right,k-1);//右子树中K-1层的节点个数
return leftNum + rightNum;
}
6、 判断两棵二叉树是否结构相同展开目录不考虑数据内容。
public class 判断两棵二叉树是否结构相同 {
/*
不考虑数据内容。结构相同意味着对应的左子树和对应的右子树都结构相同。
*/
public boolean struct(TreeNode p,TreeNode q){
if (p == null && q == null){
return true;
}else if(p == null || q == null){
return false;
}
return struct(p.left,q.left) && struct(p.right,q.right);
}
}
7、 求二叉树的镜像
public void Mirror(TreeNode root){
/*
对于每个结点,我们交换它的左右孩子即可
*/
if (root == null){
return;
}
TreeNode temp = root.left;
root.left = root.right;
root.right = temp;
Mirror(root.left);
Mirror(root.right);
}
8、求两个结点的最低公共祖先结点
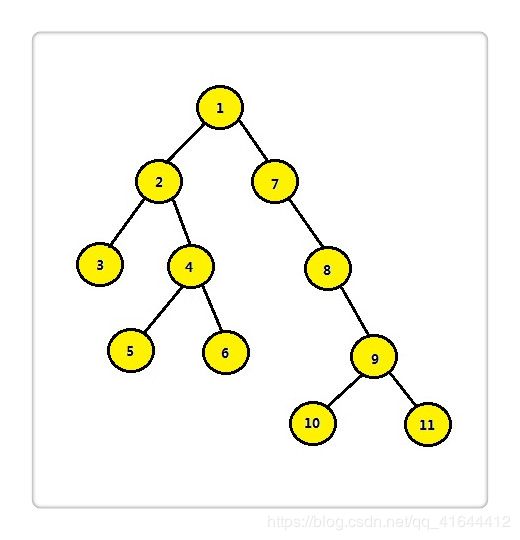
只需要判断node1和node2是否分别在左子树或者右子树上,是,返回root,否则递归到左子树和右子树
public TreeNode FindLCA(TreeNode root,TreeNode node1,TreeNode node2){
if (root == null){
return null;
}
if (root == node1 || root == node2){
return root;
}
TreeNode left = FindLCA(root.left,node1,node2);
TreeNode right = FindLCA(root.right,node1,node2);
if (left != null && right != null){ //分别在左子树和右子树上
return root;
}
return left != null ? left:right;//都在左子树或者右子树
}
9、任意两结点距离

首先找到两个结点的 LCA,然后分别计算 LCA 与它们的距离,最后相加即可。
public int Distance(TreeNode root,TreeNode node1,TreeNode node2){
TreeNode parent = FindLCA(root,node1,node2);//找两个结点的最近父节点
int dis1 = FindDistance(parent,node1);//求最近父节点到node1的距离
int dis2 = FindDistance(parent,node2);//求最近父节点到node2的距离
return dis1+dis2;
}
public int FindDistance(TreeNode node,TreeNode target){
if (node == null){
return -1;
}
if (node == target){
return 0;
}
int level = FindDistance(node.left,target);//现在左子树中找目标节点
if (level == -1){//没有
level = FindDistance(node.right, target);//在右子树中找目标节点
}
if (level != -1){//找到了目标节点,回溯求距离。没回溯一层 +1
return level+1;
}
return -1;//某的这个点
}
10、找出二叉树中某个结点的所有祖先结点
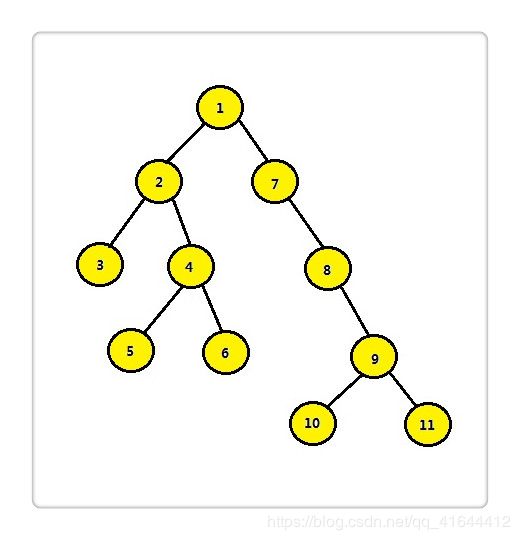
如果给定结点 5,则其所有祖先结点为 4,2,1。
public boolean FindAllParents(TreeNode root , TreeNode target){
if (root == null){
return false;
}
if (root == target){
return true;
}
if (FindAllParents(root.left,target) || FindAllParents(root.right,target)){
System.out.println(root.val);
return true;
}
return false;
}
11、线索二叉树
比较麻烦,不想搞。感兴趣可自行查看c++版
https://subetter.com/algorithm/various-operations-of-the-binary-tree.html
12、 二叉树前序中序推后序

第一步:根据前序可知根节点为A;
第二步:根据中序可知D B H E为根节点A的左子树和F C G L为根节点1的右子树;
第三步:递归实现,把D B H E当做新的一棵树和F C G L也当做新的一棵树;
第四步:根据前序遍历和中序遍历构建二叉树,按照后序遍历输出
public class Solution {
public TreeNode reConstructBinaryTree(int [] pre,int [] in) {//pre:代表前序,in:代表中序
if ((pre == null )||(in==null )){
return null;
}
TreeNode head = reConstructBinaryTree(pre,0,pre.length-1,in ,0,in.length-1);
return head;//重建的二叉树的头节点
}
private TreeNode reConstructBinaryTree(int [] pre,int preStart,int preEnd,int [] in,int inStart,int inEnd){
if (preStart> preEnd|| inStart> inEnd)
return null;
TreeNode root = new TreeNode(pre[preStart]);
for (int i=inStart;i<= inEnd;i++){
if(in[i]== pre[preStart]){
root.left=reConstructBinaryTree(pre,preStart+1,preStart + i - inStart,in,inStart,i-1);
root.right=reConstructBinaryTree(pre,preStart+1+i-inStart,preEnd,in,i+1,inEnd);
}
}
return root;
}
}
13、判断二叉树是不是完全二叉树
public class 判断二叉树是不是完全二叉树 {
/*
判断一棵树是否是完全二叉树的思路
1>如果树为空,则直接返回错
2>如果树不为空:层序遍历二叉树
2.1>如果一个结点左右孩子都不为空,则pop该节点,将其左右孩子入队列;
2.1>如果遇到一个结点,左孩子为空,右孩子不为空,则该树一定不是完全二叉树;
2.2>如果遇到一个结点,左孩子不为空,右孩子为空;或者左右孩子都为空;则该节点之后的队列中的结点都为叶子节点;
该树才是完全二叉树,否则就不是完全二叉树;
*/
public boolean IsCBT(TreeNode root){
if (root == null){
return false;
}
boolean flag = false;
LinkedList queue = new LinkedList();
queue.offer(root);
while ( !queue.isEmpty() ){
TreeNode p = queue.poll();
if (flag){ // flag为true;说明前面已经遇到含有空子结点树节点了
if (p.left != null || p.right != null){
return false;
}
}else {
if (p.left != null && p.right != null){ // 左右都不为空,放入队列
queue.offer(p.left);
queue.offer(p.right);
}else if(p.right != null){ //只有右子树,不是
return false;
}else if (p.left != null){//只有左子树,可能是,需要判断后面的结点是否全是叶子节点
queue.offer(p.left);
flag = true;
}else { // 是叶子结点
flag = true;
}
}
}
return flag;
}
14、判断是否是二叉查找树的后序遍历结果
public class 判断是否是二叉查找树的后序遍历结果 {
/*
在后续遍历得到的序列中,最后一个元素为树的根结点。从头开始扫描这个序列,比根结点小的元素都应该位于序列的左半部分;
从第一个大于跟结点开始到跟结点前面的一个元素为止,所有元素都应该大于跟结点,因为这部分元素对应的是树的右子树。
根据这样的划分,把序列划分为左右两部分,我们递归地确认序列的左、右两部分是不是都是二元查找树。
*/
public boolean IsposOrder(int[] array,int begin,int end){
if (array == null || array.length == 0){
return false;
}
if (end - begin <= 0){
return true;
}
int root_data = array[end];
int i = begin;
for (; array[i] < root_data;++i){}//找到第一个比根节点大的树
int j =i;
for (;j15、给定一个二叉查找树中的结点(存在一个指向父亲结点的指针),找出在中序遍历下它的后继和前驱
public TreeNode Increment(TreeNode node){
/*
存在一个指向父亲结点的指针:
一棵二叉查找树的中序遍历序列,正好是升序序列。假如根结点的父结点为 nullptr,则:
1、如果当前结点有右孩子,则后继结点为这个右孩子的最左孩子;
2、如果当前结点没有右孩子;
2.1. 当前结点为根结点,返回 nullptr;
2.2. 当前结点只是个普通结点,也就是存在父结点;
2.2.1. 当前结点是父亲结点的左孩子,则父亲结点就是后继结点;
2.2.2. 当前结点是父亲结点的右孩子,沿着父亲结点往上走,直到 n-1 代祖先是 n 代祖先的左孩子,则后继为 n 代祖先
或遍历到根结点也没找到符合的,则当前结点就是中序遍历的最后一个结点,返回 nullptr。
*/
if (node.right != null){//当前结点存在右子树
node = node.right;
while (node.left != null){
node = node.left;
}
}else {//不存在右子树
TreeNode p = node.parent;
while (p != null && p.right == node){//终止条件为遍历到根节点或者找到第一个是父节点的左子树的结点
node = p;
p = p.parent;
}
node = p;
}
return node;
}
16、二分查找树转化为排序的循环双链表
17、 有序链表转化为平衡的二分查找树
比较麻烦,不想写,感兴趣可自行查看c++版
https://subetter.com/algorithm/various-operations-of-the-binary-tree.html
18、判断是否是二叉查找树
public boolean IsBST(TreeNode root){
/*
利用二叉查找树中序遍历时元素递增来判断。
*/
int pre = Integer.MIN_VALUE;
if (root == null){
return true;
}
if ( !IsBST(root.left) ){
return false;
}
if (root.val < pre){
return false;
}
pre = root.val;
return IsBST(root.right);
}