3D-2D：PnP算法原理

根据高博士的《视觉SLAM十四讲》内容和相关博客的内容，对PnP问题有了一点点新的理解。再次记录一下。
参考博客：
http://www.cnblogs.com/singlex/p/pose_estimation_0.html
http://www.cnblogs.com/singlex/p/pose_estimation_1.html
http://www.cnblogs.com/singlex/p/pose_estimation_3.html

1.问题背景—— 什么是PnP问题 ？

PnP(Perspective-n-Point)是求解 3D 到 2D 点对运动的方法。它描述了当我们知道n 个 3D 空间点以及它们的投影位置时,如何估计相机所在的位姿。——《视觉SLAM十四讲》

通俗的讲，PnP问题就是在已知世界坐标系下N个空间点的真实坐标以及这些空间点在图像上的投影，如何计算相机所在的位姿。罗嗦一句：已知量是空间点的真实坐标和图像坐标，未知量（求解量）是相机的位姿。

PnP 问题有很多种求解方法，例如用三对点估计位姿的 P3P 、直接线性变换(DLT)、EPnP。此外,还能用非线性优化的方式,构建最小二乘问题并迭代求解,也就是万金油式的 Bundle Adjustment。下面介绍逐一介绍。

2.PnP问题的求解方法

2.1 P3P

2.1.1 算法的实际理解

PnP问题是在已知n 个 3D 空间点以及它们的投影位置时估计相机所在的位姿。那么 n 最小为多少时我们才能进行估算呢（最少需要几个3D-2D点对）？

我们可以设想以下场景，设相机位于点Oc，P1、P2、P3……为特征点。

场景1：N = 1时
当只有一个特征点P1，我们假设它就在图像的正中央，那么显然向量OcP1就是相机坐标系中的Z轴，此时相机永远是面对P1，于是相机可能的位置就是在以P1为球心的球面上，此外球的半径也无法确定，于是有无数个解。

场景2：N = 2时
现在多了一个约束条件，显然OcP1P2形成一个三角形，由于P1、P2两点位置确定，三角形的边P1P2确定。再加上向量OcP1和OcP2，从Oc点射向特征点的方向角也能确定。于是能够计算出OcP1的长度=r1，OcP2的长度=r2。于是这种情况下得到两个球：以P1为球心，半径为r1的球A；以P2为球心，半径为r2的球B。显然，相机位于球A，球B的相交处，依旧是无数个解。

场景3：N = 3时
这次又多了一个以P3为球心的球C，相机这次位于ABC三个球面的相交处，终于不再是无数个解了，这次应该会有4个解，其中一个就是我们需要的真解——即相机真实的位姿。

场景4：N > 3时
N=3时求出4组解，好像再加一个点就能解决这个问题了，事实上也几乎如此。说几乎是因为还有其他一些特殊情况，这些特殊情况就不再讨论了。N>3后，能够求出正解了，但为了一个正解就又要多加一个球D显然不够"环保"，为了更快更节省计算机资源地解决问题，先用3个点计算出4组解获得四个旋转矩阵、平移矩阵。根据公式：

将第四个点的世界坐标代入公式，获得其在图像中的四个投影（一个解对应一个投影），取出其中投影误差最小的那个解，就是我们所需要的正解。

2.1.2 算法的数学推导

P3P 需要利用给定的三个点的几何关系。它的输入数据为三对 3D-2D 匹配点。记 3D点为 A, B, C,2D 点为 a, b, c,其中小写字母代表的点为大写字母在相机成像平面上的投影，如上图所示。此外，P3P 还需要使用一对验证点,以从可能的解出选出正确的那一个(类似于对极几何情形)。记验证点对为 D − d,相机光心为 O。
请注意,我们知道的是A, B, C 在世界坐标系中的坐标,而不是在相机坐标系中的坐标。

首先,显然,三角形之间存在对应关系:

对于三角形Oab 和 OAB，利用余弦定理可得：

对于另外两组三角形，也有同样的结论：

对上面三式全体除以 OC^2 ，并且记 x = OA/OC， y = OB/OC，得

记 v = AB^2 /OC ^2 , uv = BC^2 /OC^2 , wv = AC^2 /OC^2 ,有:

我们可以把第一个式子中的 v 放到等式一边,并代入第 2,3 两式,得:

由于我们知道 2D 点的图像位置,三个余弦角cos ⟨a, b⟩ , cos ⟨b, c⟩ , cos ⟨a, c⟩是已知的。同时,u = BC^2 /AB^2 , w = AC^2 /AB^2 可以通过A, B, C 在世界坐标系下的坐标算出,变换到相机坐标系下之后,并不改变这个比值，所以也是已知量。该式中的 x, y 是未知的,随着相机移动会发生变化。

因此，P3P问题最终可以转换成关于 x, y 的一个二元二次方程(多项式方程)

该方程最多可能得到四个解（有上一小节也可以得出该结论）,但我们可以用验证点来计算最可能的解，得到 A, B, C 在相机坐标系下的 3D 坐标以及相机的位姿。

2.1.3 算法的缺陷

P3P 也存在着一些问题：

1. P3P 只利用三个点的信息。当给定的配对点多于 3 组时,难以利用更多的信息。
2. 如果 3D 点或 2D 点受噪声影响,或者存在误匹配,则算法失效。

所以后续人们还提出了许多别的方法，如 EPnP、 UPnP 等。它们利用更多的信息，而且用迭代的方式对相机位姿进行优化,以尽可能地消除噪声的影响。

2.2 直接线性变换(DLT)

考虑某个空间点 P ,它的齐次坐标为 P = (X, Y, Z, 1)^T 。在图像 I 中,投影到特征点 x 1 = (u 1 , v 1 , 1)^T (以归一化平面齐次坐标表示)。此时相机的位姿 R, t 是未知的。与单应矩阵的求解类似,我们定义增广矩阵 [R|t] 为一个 3 × 4 的矩阵,包含了旋转与平移信息 。我们把它的展开形式列写如下:

用最后一行把 s 消去,得到两个约束:

为了简化表示,定义 T 的行向量:

于是有:

和

请注意 t 是待求的变量,可以看到每个特征点提供了两个关于 t 的线性约束。假设一共有 N 个特征点,可以列出线性方程组:

由于 T 一共有 12 维，因此最少通过六对匹配点，即可实现矩阵 T 的线性求解，这种方法(也)称为直接线性变换(Direct Linear Transform, DLT)。当匹配点大于六对时，可以使用 SVD 等方法对超定方程求最小二乘解。

在 DLT 求解中，我们直接将 T 矩阵看成了 12 个未知数，忽略了它们之间的联系。因为旋转矩阵 R ∈ SO(3)，用 DLT 求出的解不一定满足该约束，它是一个一般矩阵。平移向量比较好办，它属于向量空间。对于旋转矩阵 R，我们必须针对 DLT 估计的 T 的左边3 × 3 的矩阵块，寻找一个最好的旋转矩阵对它进行近似。这可以由 QR 分解完成 [3, 48]，相当于把结果从矩阵空间重新投影到 SE(3) 流形上,转换成旋转和平移两部分。

需要解释的是，我们这里的 x 1 使用了归一化平面坐标，去掉了内参矩阵 K 的影响——这是因为内参 K 在 SLAM 中通常假设为已知。如果内参未知，那么我们也能用 PnP去估计 K, R, t 三个量。然而由于未知量的增多，效果会差一些。

3.实验代码

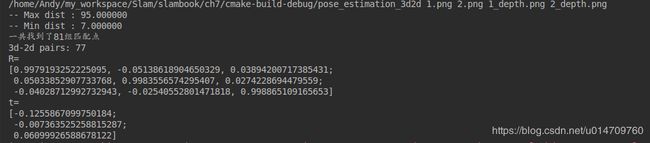
视觉slam十四讲中的代码运行结果如下：

int main ( int argc, char** argv )
{
    if ( argc != 5 )
    {
        cout<<"usage: pose_estimation_3d2d img1 img2 depth1 depth2"< keypoints_1, keypoints_2;
    vector matches;
    find_feature_matches ( img_1, img_2, keypoints_1, keypoints_2, matches );
    cout<<"一共找到了"< ( 3,3 ) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1 );
    vector pts_3d;
    vector pts_2d;

    for ( DMatch m:matches )
    {
        ushort d = d1.ptr (int ( keypoints_1[m.queryIdx].pt.y )) [ int ( keypoints_1[m.queryIdx].pt.x ) ];
        if ( d == 0 )   // bad depth
            continue;
        float dd = d/5000.0;
        Point2d p1 = pixel2cam ( keypoints_1[m.queryIdx].pt, K );
        pts_3d.push_back ( Point3f ( p1.x*dd, p1.y*dd, dd ) );
        pts_2d.push_back ( keypoints_2[m.trainIdx].pt );
    }

    cout<<"3d-2d pairs: "<

对于该代码中的BA部分，编译会出现问题：

/home/Andy/my_workspace/Slam/slambook/ch7/pose_estimation_3d2d.cpp: In function ‘void bundleAdjustment(std::vector >, std::vector >, const cv::Mat&, cv::Mat&, cv::Mat&)’:
/home/Andy/my_workspace/Slam/slambook/ch7/pose_estimation_3d2d.cpp:154:50: error: no matching function for call to ‘g2o::BlockSolver >::BlockSolver(g2o::BlockSolver >::LinearSolverType*&)’
     Block* solver_ptr = new Block ( linearSolver );     // 矩阵块求解器
                                                  ^
In file included from /usr/local/include/g2o/core/block_solver.h:199:0,
                 from /home/Andy/my_workspace/Slam/slambook/ch7/pose_estimation_3d2d.cpp:10:
/usr/local/include/g2o/core/block_solver.hpp:40:1: note: candidate: g2o::BlockSolver::BlockSolver(std::unique_ptr) [with Traits = g2o::BlockSolverTraits<6, 3>; typename Traits::LinearSolverType = g2o::LinearSolver >]
 BlockSolver::BlockSolver(std::unique_ptr linearSolver)
 ^
/usr/local/include/g2o/core/block_solver.hpp:40:1: note:   no known conversion for argument 1 from ‘g2o::BlockSolver >::LinearSolverType* {aka g2o::LinearSolver >*}’ to ‘std::unique_ptr >, std::default_delete > > >’
/home/Andy/my_workspace/Slam/slambook/ch7/pose_estimation_3d2d.cpp:155:104: error: no matching function for call to ‘g2o::OptimizationAlgorithmLevenberg::OptimizationAlgorithmLevenberg(Block*&)’
     g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg ( solver_ptr );
                                                                                                        ^
In file included from /home/Andy/my_workspace/Slam/slambook/ch7/pose_estimation_3d2d.cpp:11:0:
/usr/local/include/g2o/core/optimization_algorithm_levenberg.h:47:16: note: candidate: g2o::OptimizationAlgorithmLevenberg::OptimizationAlgorithmLevenberg(std::unique_ptr)
       explicit OptimizationAlgorithmLevenberg(std::unique_ptr solver);
                ^
/usr/local/include/g2o/core/optimization_algorithm_levenberg.h:47:16: note:   no known conversion for argument 1 from ‘Block* {aka g2o::BlockSolver >*}’ to ‘std::unique_ptr’
/home/Andy/my_workspace/Slam/slambook/ch7/pose_estimation_3d2d.cpp:156:42: error: redeclaration of ‘g2o::OptimizationAlgorithmLevenberg* solver’
     g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg(std::move(solver_ptr));
                                          ^
/home/Andy/my_workspace/Slam/slambook/ch7/pose_estimation_3d2d.cpp:155:42: note: ‘g2o::OptimizationAlgorithmLevenberg* solver’ previously declared here
     g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg ( solver_ptr );
                                          ^
/home/Andy/my_workspace/Slam/slambook/ch7/pose_estimation_3d2d.cpp:156:112: error: no matching function for call to ‘g2o::OptimizationAlgorithmLevenberg::OptimizationAlgorithmLevenberg(std::remove_reference >*&>::type)’
     g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg(std::move(solver_ptr));
                                                                                                                ^
In file included from /home/Andy/my_workspace/Slam/slambook/ch7/pose_estimation_3d2d.cpp:11:0:
/usr/local/include/g2o/core/optimization_algorithm_levenberg.h:47:16: note: candidate: g2o::OptimizationAlgorithmLevenberg::OptimizationAlgorithmLevenberg(std::unique_ptr)
       explicit OptimizationAlgorithmLevenberg(std::unique_ptr solver);
                ^
/usr/local/include/g2o/core/optimization_algorithm_levenberg.h:47:16: note:   no known conversion for argument 1 from ‘std::remove_reference >*&>::type {aka g2o::BlockSolver >*}’ to ‘std::unique_ptr’
CMakeFiles/pose_estimation_3d2d.dir/build.make:62: recipe for target 'CMakeFiles/pose_estimation_3d2d.dir/pose_estimation_3d2d.cpp.o' failed
make[3]: *** [CMakeFiles/pose_estimation_3d2d.dir/pose_estimation_3d2d.cpp.o] Error 1
CMakeFiles/Makefile2:72: recipe for target 'CMakeFiles/pose_estimation_3d2d.dir/all' failed
make[2]: *** [CMakeFiles/pose_estimation_3d2d.dir/all] Error 2
CMakeFiles/Makefile2:84: recipe for target 'CMakeFiles/pose_estimation_3d2d.dir/rule' failed
make[1]: *** [CMakeFiles/pose_estimation_3d2d.dir/rule] Error 2
Makefile:118: recipe for target 'pose_estimation_3d2d' failed
make: *** [pose_estimation_3d2d] Error 2

参照g2o官方示例和相关博客，可以做如下修改：

//源代码
    // 初始化g2o
    /*typedef g2o::BlockSolver< g2o::BlockSolverTraits<6,3> > Block;  // pose 维度为 6, landmark 维度为 3
    Block::LinearSolverType* linearSolver = new g2o::LinearSolverCSparse(); // 线性方程求解器
    Block* solver_ptr = new Block ( linearSolver );     // 矩阵块求解器
    g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg ( solver_ptr );
    g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg(std::move(solver_ptr));
    */

    //仿照g2o示例中的代码进行修改——可以运行
    auto linearSolver = g2o::make_unique>();
    auto solver_ptr = g2o::make_unique(std::move(linearSolver));
    OptimizationAlgorithmLevenberg* solver = new OptimizationAlgorithmLevenberg(std::move(solver_ptr));

    //网上的修改意见——可以运行
    /*typedef g2o::BlockSolver< g2o::BlockSolverTraits<6,3> > Block;  // pose 维度为 6, landmark 维度为 3
    std::unique_ptr linearSolver ( new g2o::LinearSolverCSparse()); // 线性方程求解器
    std::unique_ptr solver_ptr ( new Block ( std::move(linearSolver)));     // 矩阵块求解器
    g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg ( std::move(solver_ptr));
    */

    g2o::SparseOptimizer optimizer;
    optimizer.setAlgorithm ( solver );

成功编译后，结果如下：