HDP(层次狄利克雷过程)算法代码实现细节梳理(Java)
本文作者:合肥工业大学 电子商务研究所 钱洋 email:[email protected] 。
内容可能有不到之处,欢迎交流。
未经本人允许禁止转载。
文章目录
- HDP简介
- 有向图表示
- CRF的关键
- HDP的采样
- 编程角度解读
- 采样桌子
- 采样主题
- 完整代码
- 参考
HDP简介
Teh Y W, Jordan M I, Beal M J, et al. Sharing clusters among related groups: Hierarchical Dirichlet processes[C]//Advances in neural information processing systems. 2005: 1385-1392.
来自于2005年,NIPS。HDP可以说是做非参贝叶斯推理必须的模型。
学习该模型前,需要了解DP以及DP的构造方式(stick-breaking construction)。
针对DP过程,其对应求解策略为中餐馆过程 ;针对HDP,其求解策略为中餐馆连锁(CRF,Chinese restaurant franchise)。
关于DP和HDP的学习也可以参照我之前写的几篇博客:
中餐馆过程:https://blog.csdn.net/qy20115549/article/details/52371443
我个人分享的PPT:Dirichlet Process和Hierarchical Dirichlet Process的理解(https://blog.csdn.net/qy20115549/article/details/79663483)
Dirichlet Process and Stick-Breaking:https://blog.csdn.net/qy20115549/article/details/62041632
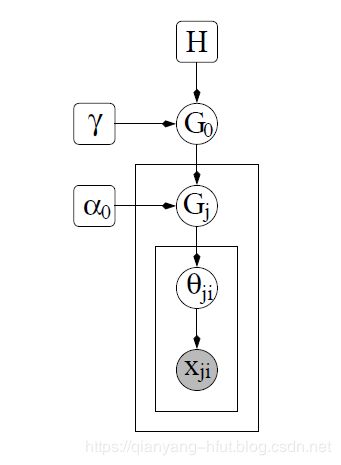
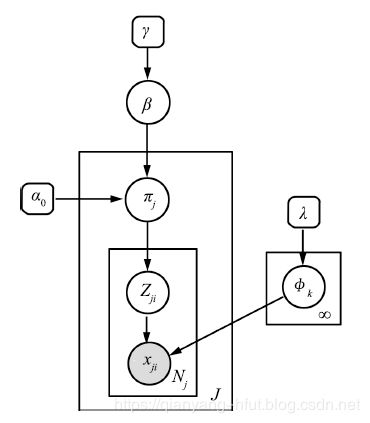
有向图表示
CRF的关键
HDP之所以使用中餐馆连锁求解,其原因保证餐馆(文档)与餐馆之间是共享菜单(主题)的,这一点非常关键。如果不能保证共享主题,也就无法进行主题的发现。如下为CRF的示意图。该图来自于中科院曾大军研研究团队。
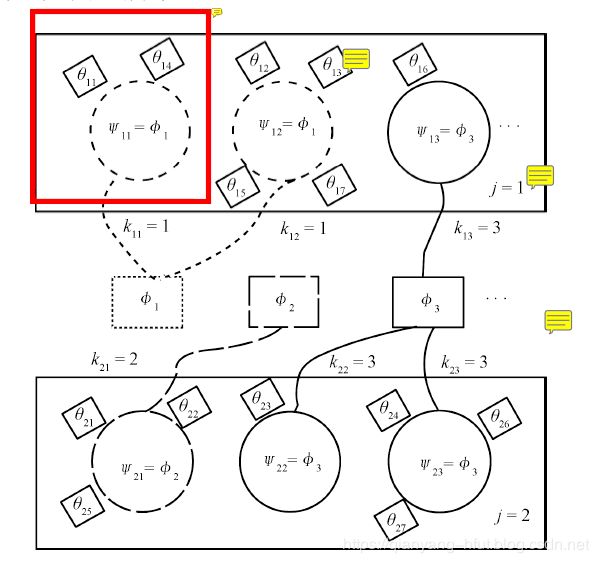
下图,为本人总结的CRF的特点:
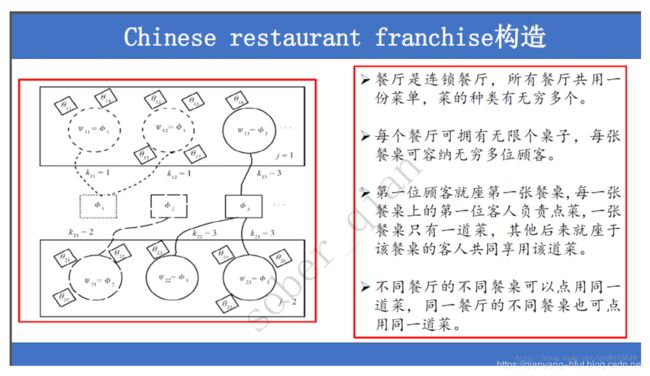
HDP的采样
HDP的采样有多样,其中使用比较多的便是Collapsed Gibbs Sampling。其采样共分为两个层次,可参考我的PPT,这里直接上图:

其中,顾客对应的是每篇文档的每个词。

对于每个顾客,可以选择旧桌子就坐,概率和桌子上的人数成正比,也可以选择一张新桌子就坐。需要注意的是:**如果选择的旧桌子,该顾客就不用点菜了,即文档该词对应的主题和桌子原有的主题一致,不更新**。
如果选择了新桌子,那么则需要进行下一步,为其分配一道菜,即主题。
这种策略也就是编程实现的核心思想。
编程角度解读
采样桌子
如下为编程需要使用到的第一个公式:

该项表示新桌子生成单词的概率。
针对这个公式,我们可以看到,在编程时需要统计的变量包括: p ( x j i ∣ . . . ) p\left ( x_{ji}|... \right ) p(xji∣...),所有预料中主题 k k k对应的桌子总数目 m ⋅ k m_{\cdot k} m⋅k,语料中桌子的总数目 m ⋅ ⋅ m_{\cdot \cdot} m⋅⋅,观测数据的条件概率分布 f k − x j i ( ⋅ ) f_{k}^{-x_{ji}}\left ( \cdot \right ) fk−xji(⋅)和 f k n e w − x j i ( ⋅ ) f_{k^{new}}^{-x_{ji}}\left ( \cdot \right ) fknew−xji(⋅)。
注意观测数据的条件概率分布为:
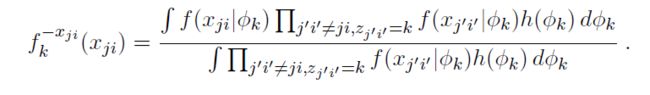
这个公式看起来很复杂。但实际上,其和LDA的生成词的过程是一致的,利用共轭分布的性质是可以直接得到的。
如下为采样桌子的公式:
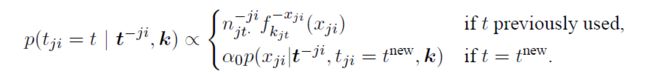
基于这个公式,可以看到编程需要统计的变量有:文档桌子对应的词汇数量 n j t ⋅ − j i n_{jt\cdot }^{-ji} njt⋅−ji和用于轮盘赌的变量 p ( t j i = t ) p\left ( t_{ji}=t \right ) p(tji=t)。
/**
* sample a table for a word
*
* new table or old table
*
* if new table, choose a topic for this table
*/
int sampleTable(int d, int n) {
double pSum = 0.0;
f = ensureCapacity(f, K);
p = ensureCapacity(p, ndtable[d]);
double fNew = gamma / V;
for (int k = 0; k < K; k++) {
f[k] = (nkw[k][docword[d][n]] + beta) /
(nksum[k] + V*beta);
fNew += nk_table[k] * f[k];
}
for (int tab = 0; tab < ndtable[d]; tab++) {
if (ndtable_wordCount[d][tab] > 0)
pSum += ndtable_wordCount[d][tab] * f[d_tableToTopic[d][tab]];
p[tab] = pSum;
}
pSum += alpha * fNew / (totalTablesNum + gamma); // Probability for t = tNew
p[ndtable[d]] = pSum;
double u = (new Random()).nextDouble() * pSum;
int j;
for (j = 0; j <= ndtable[d]; j++)
if (u < p[j])
break; // which table assignment for the word
return j;
}
由于非参模型,其主体数目和每篇文档的桌子数目是在不断变化的。因此需要注意和桌子统计相关的变量、和主题相关的变量要扩容,以防止数组操作越界。
采样主题
如果文档中的某单词背分配了新桌子,那么则需要对该桌子分配一个主题,如果为采样公式:
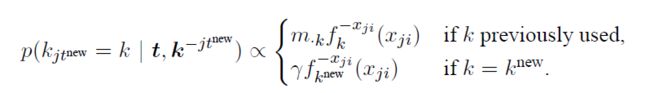
从这个公式中,可以看到编程时需要统计的变量有: p ( k j t n e w = k ) p\left ( k_{jt^{new}}=k \right ) p(kjtnew=k)。
如下为对应的Java代码:
/**
*
* if new table, choose a topic for this table
*
*/
private int sampleTopic() {
double pSum = 0.0;
p = ensureCapacity(p, K);
for (int k = 0; k < K; k++) {
pSum += nk_table[k] * f[k];
p[k] = pSum;
}
pSum += gamma/ V;
p[K] = pSum;
double u = (new Random()).nextDouble() * pSum;
int k;
for (k = 0; k <= K; k++)
if (u < p[k])
break;
return k;
}
完整代码
本人的完整代码,会在之后上传到Github中,即本人所编写的TopicModel4J:https://github.com/soberqian/TopicModel4J
模型的使用方式:
public static void main(String[] args) {
HDP hdp = new HDP("data/rawdata_process_lda", "gbk", 10, 1, 0.01,
0.1, 1000, 50, "data/ldaoutput/");
hdp.MCMCSampling();
}
调用该模型非常的简单,只需要输入文件目录和输入目录以及HDP的参数就行。
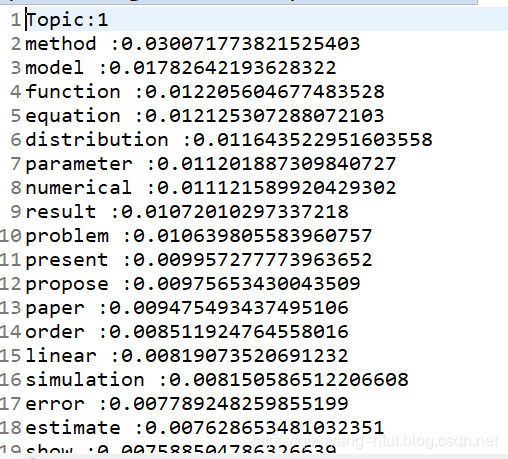
输入包括文档主题分布和主题词分布,例如:
参考
周建英, 王飞跃, 曾大军. 分层 Dirichlet 过程及其应用综述[J]. 自动化学报, 2011, 37(4): 389-407.