Matlab下 IIR 滤波器实现(Simulink仿真和C语言实现)
经典滤波器和现代滤波器
一般滤波器可以分为经典滤波器和现代滤波器。
- 经典滤波器:假定输入信号中的有用成分和希望去除的成分各自占有不同的频带。如果信号和噪声的频谱相互重迭,经典滤波器无能为力。比如 FIR 和 IIR 滤波器等。
- 现代滤波器:从含有噪声的时间序列中估计出信号的某些特征或信号本身。现代滤波器将信号和噪声都视为随机信号。包括 Wiener Filter、Kalman Filter、线性预测器、自适应滤波器等
Z变换和差分方程
在连续系统中采用拉普拉斯变换求解微分方程,并直接定义了传递函数,成为研究系统的基本工具。在采样系统中,连续变量变成了离散量,将Laplace变换用于离散量中,就得到了Z变换。和拉氏变换一样,Z变换可用来求解差分方程,定义Z传递函数成为分析研究采样系统的基本工具。
对于一般常用的信号序列,可以直接查表找出其Z变换。相应地,也可由信号序列的Z变换查出原信号序列,从而使求取信号序列的Z变换较为简便易行。
Z变换有许多重要的性质和定理:
-
线性定理
设a,a1,a2为任意常数,连续时间函数f(t),f1(t),f2(t)的Z变换分别为F(z),F1(z),F2(z),则有
Z[a*f(t)]=aF(z)
Z[a1f1(t)+a2f2(t)]=a1F1(z)+a2F2(z)
-
滞后定理
设连续时间函数在t<0时,f(t)=0,且f(t)的Z变换为F(z),则有
Z[f(t−kT)]=z^−k * F(z)
IIR数字滤波器结构
IIR滤波器常见的结构形式有直接Ⅰ型、直接Ⅱ型(典范型)、级联型、并联型。通过差分方程能够画出包含反馈结构的数字网络称为直接型。
直接Ⅰ型滤波器的网络结构可以根据差分方程很直观地画出(The Direct-Form I structure implements the feed-forward terms first followed by the feedback terms):
可以看出直接Ⅰ型滤波器需要N+M个延时单元(N≥M)。直接Ⅱ型结构是对直接Ⅰ型的变型,将上面网络的零点与极点的级联次序互换,并将延时单元合并。实现N阶滤波器只需要N个延时单元(The Direct-Form II structure uses fewer delay blocks than Direct-Form I),故称为典范型。
直接Ⅱ型看上去不那么直观,可以通过下图进行理解。我们可以将整个滤波器系统看成A、B两个子系统串联而成,由于为线性系统因此交换顺序不影响最终输出结果,传递函数可写为:
H(z)=B(z)*1/A(z)=1/A(z)*B(z)
直接型优点:直接型结构简单,用的延迟器较少(N和M中较大者的个数);缺点:系数ak,bk对滤波器性能的控制关系不直接,因此调整不方便;具体实现滤波器时ak,bk的量化误差将使滤波器的频率响应产生很大的改变,甚至影响系统的稳定性。直接型结构一般用于实现低阶系统。
级联型:将系统传递函数H(z)因式分解为多个二阶子系统,系统函数就可以表示为这些二阶子系统传递函数的乘积。实现时将每个二阶子系统用直接型实现,整个系统函数用二阶环节的级联实现。
并联型:与级联型类似,用部分分式展开法将系统函数表示为二阶子系统传递函数的和。每个二阶子系统仍然用直接型实现,整个系统函数用二阶环节的并联实现。
FDATool工具
在IIR滤波器设计过程中,通常利用模拟滤波器来设计数字滤波器,要先根据滤波器的性能指标设计出相应的模拟滤波器的系统函数H(s),然后由H(s)经变换得到所需要的数字滤波器的系统函数H(z)。常用的变换方法有冲激响应不变法和双线性变换法。下面使用MATLAB等工具直接生成数字滤波器系数:
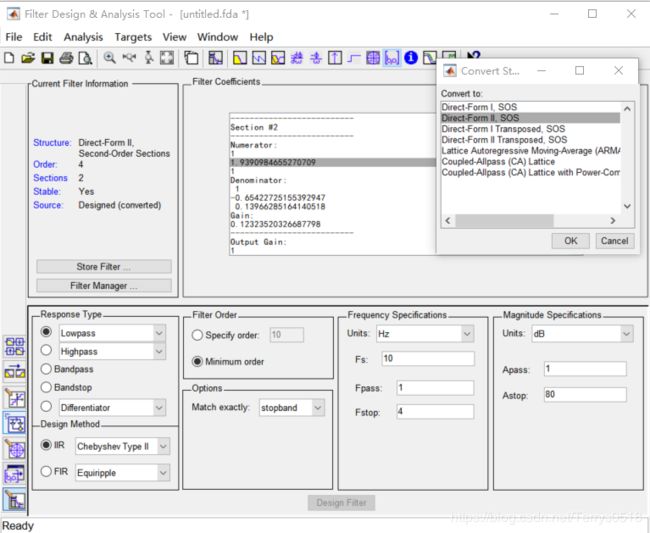
在MATLAB命令行中输入fdatool打开滤波器设计工具箱,为了便于分析,我们先从设计一个简单的2阶低通滤波器。Design Method用于选择IIR滤波器还是FIR滤波器,这里我们选择IIR滤波器,类型选择Chebyshev TypeII,当然也可以选择其他类型,不同类型的频率响应不同,选择后默认的滤波器结构是直接II型。ResponseType用于选择低通、高通、带通、带阻等类型,选择低通滤波“Lowpass”。Frequency Specifications用于设置采样频率以及截止频率,这里填入Fs = 10 Fpass = 1,Fstop = 4 即采样率为10Hz,1Hz以上的频率将被滤除掉。Fiter Order 选择滤波器阶数,为了简单起见,先选择一个2阶滤波器做实验。
参数设置好后点击Design filter按钮,将按要求设计滤波器。默认生成的IIR滤波器类型是Direct-Form II,Second-Order Sections(直接Ⅱ型,每个Section是一个二阶滤波器),在工具栏上点击Filter Coefficients图标或菜单栏上选择Analysis→Filter Coefficients可以查看生成的滤波器系数。菜单栏上选择Edit->Convert Structure 可以查看滤波器结构类型 Direct-Form II SOS。
MATLAB中二阶滤波器差分方程公式如下(注意反馈项符号为负号):
y[n]=b0⋅x[n]+b1⋅x[n−1]+b2⋅x[n−2]−a1⋅y[n−1]−a2⋅y[n−2]
如上图Section的公式如下
y[n] = x[n] + 1.9390984655⋅x[n−1]+x[n−2] - (-0.654227)⋅y[n−1]−0.123235⋅y[n−2]
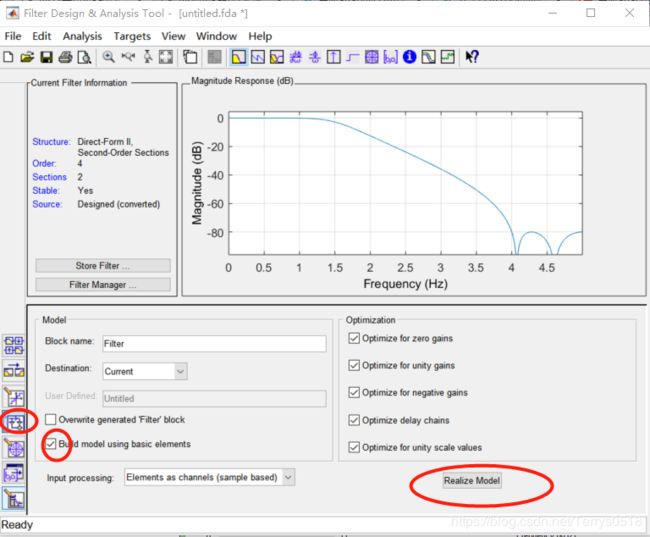
滤波器设计完成后还可以生成Simulink模型进行仿真:按照下图中数字标号进行,第一步点击左边Realize Model图标,第二步勾选“Build model using basic elements”这一项,右边四个灰色的项将自动打钩,最后点击“Realize Model”,matlab将自动生成滤波器模型,在弹出的窗口中双击模型可以观察该模型的内部结构。
下面是直接Ⅱ型的内部结构
Simulink仿真
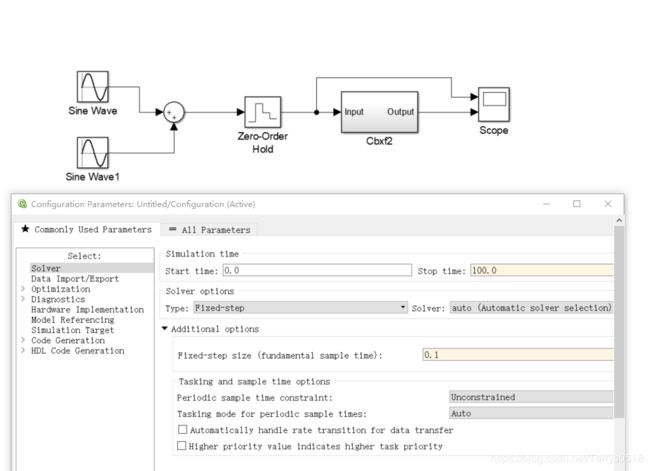
使用生成的滤波器搭建一个简答的测试模型:将两个幅值为1,频率分别为 0.5Hz 和 3Hz正弦波信号,数字量化0.1秒
解算器步长 0.1 ,时间 10秒(下图为100秒)
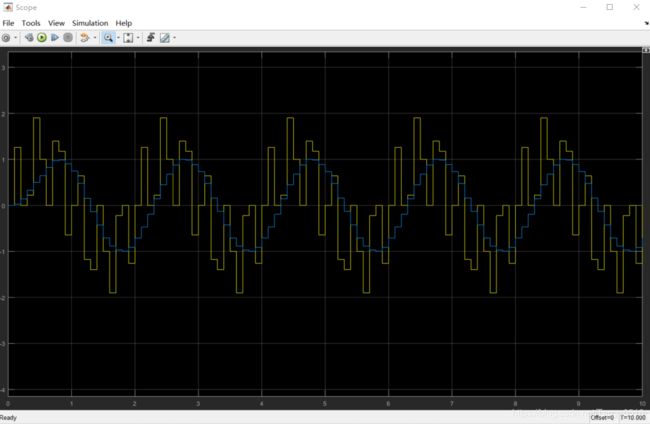
黄线为输入正弦波量化叠加信号,蓝线为滤波器输出信号
滤波器C语言代码如下:
matlab 生成的C语言头文件 iirchb3.h
* Generated by MATLAB(R) 9.0 and the Signal Processing Toolbox 7.2.
* Generated on: 15-Jan-2019 09:38:15
*/
/*
* Discrete-Time IIR Filter (real) 注意,这里是直接2型
* -------------------------------
* Filter Structure : Direct-Form II, Second-Order Sections
* Number of Sections : 2
* Stable : Yes
* Linear Phase : No
*/
/* General type conversion for MATLAB generated C-code */
#include "tmwtypes.h"
/*
* Expected path to tmwtypes.h
* C:\Program Files\MATLAB\R2016a\extern\include\tmwtypes.h
*/
/*
* Warning - Filter coefficients were truncated to fit specified data type.
* The resulting response may not match generated theoretical response.
* Use the Filter Design & Analysis Tool to design accurate
* single-precision filter coefficients.
*/
#define MWSPT_NSEC 5
const int NL[MWSPT_NSEC] = { 1,3,1,3,1 };
const float IIR_B[MWSPT_NSEC][3] = {
{
0.1747451723, 0, 0
},
{
1, 1.669347644, 1
},
{
0.1232352033, 0, 0
},
{
1, 1.939098477, 1
},
{
1, 0, 0
}
};
const int DL[MWSPT_NSEC] = { 1,3,1,3,1 };
const float IIR_A[MWSPT_NSEC][3] = {
{
1, 0, 0
},
{
1, -0.8880870342, 0.5292878151
},
{
1, 0, 0
},
{
1, -0.6542272568, 0.1396628469
},
{
1, 0, 0
}
};#include “iirchb3.h” /* matlab 生成滤波器头文件 */
float cc[181] = {111.3, 569.2, 947.7, 915.1, 1033.8, 1052.5, 1105.5, 1102.8, 1047.3, 1186.5, 1067.1, 1074.5, 1093.1, 1169.4, 1078.1, 1146.6, 1099.6, 1036.7, 1150.9, 1052.7, 1119.7, 1115.1, 1054.6, 1175.4, 1108.1, 1009.8, 1130.8, 1124.5, 1038.1, 1007.7, 1128.0, 1148.9, 1080.2, 980.4, 1080.3, 1193.5, 1016.6, 1244.6, 1261.7, 1148.6, 1145.1, 1138.0, 1076.6, 1018.1, 1032.6, 1055.5, 1152.3, 1157.4, 1141.2, 1064.9, 1069.9, 1059.6, 1089.9, 1047.5, 1027.2, 1074.4, 1142.6, 1064.9, 1199.2, 1114.6, 1081.9, 1089.5, 1121.0, 1052.0, 1058.1, 1198.8, 1108.4, 1022.1, 1207.1, 1128.8, 1177.5, 1199.4, 1129.3, 1062.1, 1184.5, 1151.7, 1144.7, 1152.8, 1136.7, 1195.6,1217.3, 1143.2, 1133.7, 1185.2, 1082.5, 1177.8, 1212.2, 1155.6, 1162.0, 1183.5, 1152.3, 1226.2, 1210.5, 1175.2, 1256.6, 1184.0, 1172.1, 1175.1, 1237.0, 1254.7, 1232.5, 1236.5, 1275.8, 1194.5, 1197.2, 1156.1, 1248.8,
1213.2, 1244.0, 1249.8, 1260.8, 1276.0, 1216.2, 1220.7, 1250.3, 1283.3, 1349.2, 1326.3, 1308.6, 1238.0, 1275.5, 1238.0, 1226.9, 1256.5, 1171.0, 1275.6,
1328.5, 1234.5, 1219.8, 1153.1, 1178.0, 1243.7, 1182.2, 1172.9, 1260.7, 1230.5, 1215.3, 1212.7, 1201.0, 1197.6, 1234.6, 1243.4, 1212.5, 1235.4, 1238.6,
1228.0, 1167.0, 1221.0, 1249.2, 1234.5, 1245.9, 1224.2, 1167.4, 1264.5, 1166.0, 1219.0, 1222.2, 1180.7, 1369.5, 1276.7, 1212.3, 727.4, 436.4, 261.9,
157.1, 94.3, 56.6, 33.9, 20.4, 12.2, 7.3, 4.4, 2.6, 1.6, 0.9, 0.6, 0.3, 0.2, 0.1, 0.1, 0.0};
static float xlast[2];
static float mlast[2]; //中间节点
//二阶IIR滤波器 参考直接Ⅱ型的内部结构
static float IIR_DR2(float x,float *plast,const float (*A)[3],const float (*B)[3])
{
float tmp,last;
tmp = x * B[0][0];
last = tmp - (A[1][1] * plast[0] + A[1][2] * plast[1]);
tmp = last + (B[1][1] * plast[0] + B[1][2] * plast[1]);
plast[1] = plast[0];
plast[0] = last;
return tmp;
}
//二阶滤波器组合成更高阶数的滤波器
float IIR_Filter(float x)
{
float mid,y;
mid = IIR_DR2(x,xlast,IIR_A,IIR_B);
y = IIR_DR2(mid,mlast,&IIR_A[2],&IIR_B[2]);
//更多阶数...
return y;
}
//滤波器复位
void Init_Filter(void)
{
xlast[0] = 0;
xlast[1] = 0;
mlast[0] = 0;
mlast[1] = 0;
}
int main()
{
int i;
for(i = 0;i<181;i++)
printf("%.1f, ",IIR_Filter(cc[i]));
return 0;
}
检验C代码
原始信号
滤波后的信号