八数码问题求解

参考博客

算法实现多是参考博客中的代码，加上注释有助于自己的理解和巩固。

问题介绍

解决方法：

（1）将初始节点S0放置到open表中，F(s0)=g(s0)+h(s0)//当前深度和错误数之和
（2）如果open表为空，搜索失败
（3）把open表中的第一个节点放置到closed表中，并计该节点为n
（4）考察节目标点n是否为目标节点。如果是则找到目标节点，退出系统
（5）如果考察的节点无法扩展，则进行第二步
（6）扩展节点n，生成子节点ni(i=1，2，3，4....)计算每一个子节点的估值，
  并为每个子节点设置指向父节点的指针，然后将这些子节点放置到open表中
  然后根据各节点的值进行排序，对其中各节点按照从小到大的顺序进行排序
（7）转第二步

程序中要用的函数和一些知识点

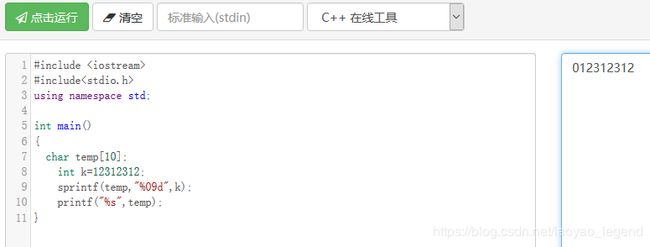
1.sprintf(char,char,...)函数

int sprintf( char *buffer, const char *format [, argument,...] );

 sprintf的功能时将信息输入到字符串中

除了前两个参数固定外，可选参数可以是任意个。buffer是字符数组名；format是格式化字符串（像："%3d%6.2f%#x%o",%与#合用时，自动在十六进制数前面加上0x）。只要在printf中可以使用的格式化字符串，在sprintf都可以使用。其中的格式化字符串是此函数的精华。

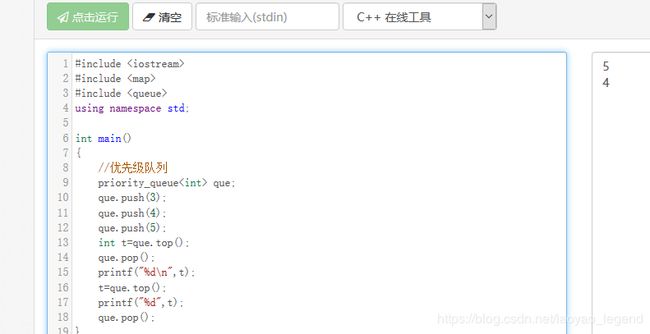
 3.优先级队列priority_queue队列

值由大到小排列

可见sprintf函数是将k中的值传到字符串temp中去了。

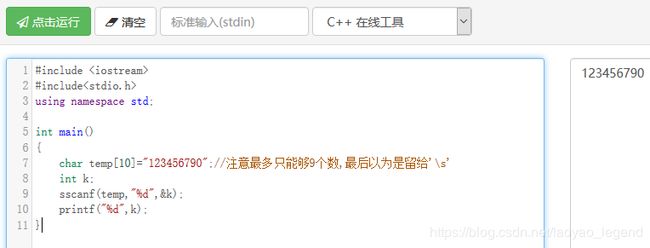
2.sscanf(char,char,...)函数的使用

int sscanf(const char *buffer,const char *format,[argument ]...);

buffer存储的数据
format格式控制字符串
argument选择性设定字符串
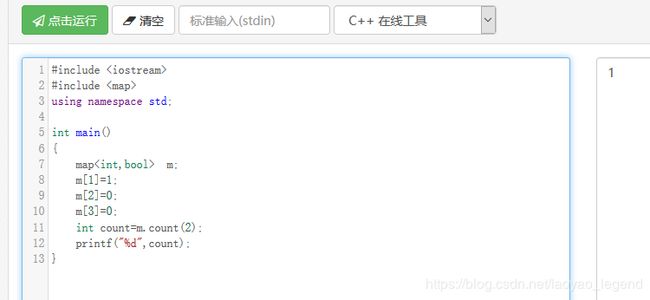
sscanf会从buffer里读进数据，依照format的格式将数据写入到argument里

3.map中的count( object )函数

返回的是被查找目标的是否存在，如果存在则返回1,否则返回0

Code (thanks for yqw999's blog)

建立节点数据结构

struct node 
{
	int num;//记录点
	int step;//当前节点所在的深度
	int cost;//估价值  深度+错误值
	int zeroPos;//零所在的位置
	//重载运算符
	bool operator <(const node &a) const//比较优先级
	{
		return cost > a.cost;//根据定义，cost小的优先级越高
	}
	node(int n, int s, int p)//构造函数
	{
		num = n;//记录数据的排列
		step = s;//深度
		zeroPos = p;//零所在的位置
		SetCost();//重置估价值
	}
	void SetCost() //计算估价值：当前深度+错误值
	{
		char a[10];
		int c = 0;//用来盛放错误值
		sprintf(a,"%09d",num);
		
		for (int i = 0; i < 9; i++)
		{
			if (a[i] != brr[i]) c++;//计算错误值
		}
		cost = c + step;//所得估计值
	}

};

每一个位置都有一个移动的范围，可上下左右移动，我们用-1表示不能移动。

int changeId[9][4] = { { -1,-1,3,1 },{ -1,0,4,2 },{ -1,1,5,-1 },
{ 0,-1,6,4 },{ 1,3,7,5 },{ 2,4,8,-1 },
{ 3,-1,-1,7 },{ 4,6,-1,8 },{ 5,7,-1,-1 } };

 搜索的算法实现

基本原理实现的是首先将初始节点压入优先级队列中进行扩展，将可以扩展的（不重复）的节点压入优先级队列中。每次都选择优先级最高的（其实也就是估价值最小的）进行扩展，当扩展到目标节点的时候，返回，搜索完成。

int bfsHash(int start, int zeroPos)//开始状态，零所在的位置
{
	char temp[10];
	node tempN(start, 0, zeroPos);//开始时深度为零--创建第一个节点
	que.push(tempN);//将第一个节点放入优先级队列中
	mymap[start] = 1;//将此节点标记为已访问
	if (start == des) return 0;//开始状态即为结束状态
	while (!que.empty())//如果open表不为空
	{
		int k1;
		tempN = que.top();//获得一个顶点节点
		que.pop();//弹出一个节点 
		printf("选择扩展的父节点为%09d\n", tempN.num);
		sprintf(temp, "%09d", tempN.num);//将tempN.num输出到temp中
		int pos = tempN.zeroPos, k;
		for (int i = 0; i < 4; i++)
		{
			if (changeId[pos][i] != -1) 
			{
				swap(temp, pos, changeId[pos][i]);
				sscanf(temp, "%d", &k);
				//printf("%s\n", temp);
				if (k == des)return tempN.step + 1;
				if (mymap.count(k) == 0)//此节点是不存在closed表中
				{
					node tempM(k, tempN.step + 1, changeId[pos][i]);
					printf("扩展:当前深度%d----值为%09d\n",tempN.step+1, k);
					que.push(tempM);//创建一个新节点并压入队列 
					mymap[k] = 1;
				}
				//printf("%s\n", temp);
				swap(temp, pos, changeId[pos][i]);//进行循环操作，直到k==des 
			}
		}
	}
	return -1;
}

判断有无解要用的知识---逆序数

八数码问题的有解无解的结论：

一个状态表示成一维的形式，求出除0之外所有数字的逆序数之和，也就是每个数字前面比它大的数字的个数的和，称为这个状态的逆序。

若两个状态的逆序奇偶性 相同，则可相互到达，否则不可相互到达。---参考博客

// 判断逆序数的奇偶性
bool inverNum(char ch[])
{
	int sum = 0;
	for (int i = 0; i < 9; i++)
	{
		if (ch[i] != '0') {
			int dsum = 0;
			for (int j = 0; j < i; j++)
				if (ch[i] < ch[j]) dsum++;
			sum += dsum;
		}
		
	}
	return sum%2;
}

完整代码

#include "stdafx.h"
//创建实现八数码的程序

#include
#include

以上是我的学习笔记，博客参考---八数码问题大神博客