【Python】BFS广度优先搜索解决权值相同的最短路径问题
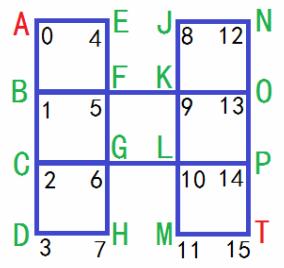
BFS广度优先搜索 示例：
给定如图所示的无向连通图，假定图中所有边的权值都为1，显然，从源点A到终点T的最短路径有多条，求不同的最短路径
算法分析
权值相同的最短路径问题，则单源点 Dijkstra 算法退化成 BFS 广度优先搜索，假定起点为 0，终点为 N：
结点步数 step[0…N-1] 初始化为 0
若从当前结点 i 扩展到邻接点 j 时：
若 step[ j ] 为 0，则
step[ j ] = step[ i ] + 1，到结点 j 的路径就 = 到结点 i 的路径 + 结点 j
若 step[ j ] == step[ i ] + 1，则
到结点j的路径就 = 到结点 j 的路径就 + ( 到结点 i 的路径 + 结点 j )
可考虑一旦扩展到结点N，则提前终止算法
Python代码如下：
import numpy as np
from copy import deepcopy
# 获取到各个结点的最短线路
def get_path(g):
n = len(g)
step = [0 for i in range(n)] # 每个结点第几步可以到达
step_path = [[] for i in range(n)] # 到每个结点的走法
step_path[0] = [[0]] # 到结点0有1种走法
q = [0] # 当前搜索的结点
while len(q) > 0:
f = q.pop() # f就是from的结点
s = step[f] + 1
for i in range(1, n): # 0是起点，不遍历
if g[f][i] == 1: # 从结点f到结点i连通
# i尚未可达或发现更快的路径（权值不同才有可能）
if (step[i] == 0) or (step[i] > s):
step[i] = s
q.insert(0, i)
step_path[i] = deepcopy(step_path[f])
if len(step_path[i]) > 0:
for j in range(len(step_path[i])):
step_path[i][j].append(i) # 线路中添加结点i
elif step[i] == s: # 发现相同长度的路径
dp = deepcopy(step_path[f])
if len(dp) > 0:
for j in range(len(dp)):
dp[j].append(i) # 线路中添加结点i
step_path[i] += dp
return step_path
if __name__ == '__main__':
# 初始化图的数据，连通的标记为1
g = np.zeros(shape=(16, 16), dtype='int')
g[0][1] = g[0][4] = 1
g[1][0] = g[1][2] = g[1][5] = 1
g[2][1] = g[2][3] = g[2][6] = 1
g[3][2] = g[3][7] = 1
g[4][0] = g[4][5] = 1
g[5][1] = g[5][4] = g[5][6] = g[5][9] = 1
g[6][2] = g[6][5] = g[6][7] = g[7][10] = 1
g[7][3] = g[7][6] = 1
g[8][9] = g[8][12] = 1
g[9][5] = g[9][8] = g[9][10] = g[9][13] = 1
g[10][6] = g[10][9] = g[10][11] = g[10][14] = 1
g[11][10] = g[11][15] = 1
g[12][8] = g[12][13] = 1
g[13][9] = g[13][12] = g[13][14] = 1
g[14][10] = g[14][13] = g[14][15] = 1
g[15][11] = g[15][14] = 1
step_path = get_path(g)
# 输出结果
for i in range(len(step_path)):
size = len(step_path[i])
print('到结点%s的最短路径%s条：' % (i, size))
for j in range(size):
print(step_path[i][j])输出结果：
到结点0的最短路径1条：
[0]
到结点1的最短路径1条：
[0, 1]
到结点2的最短路径1条：
[0, 1, 2]
到结点3的最短路径1条：
[0, 1, 2, 3]
到结点4的最短路径1条：
[0, 4]
到结点5的最短路径2条：
[0, 1, 5]
[0, 4, 5]
到结点6的最短路径3条：
[0, 1, 2, 6]
[0, 1, 5, 6]
[0, 4, 5, 6]
到结点7的最短路径4条：
[0, 1, 2, 3, 7]
[0, 1, 2, 6, 7]
[0, 1, 5, 6, 7]
[0, 4, 5, 6, 7]
到结点8的最短路径2条：
[0, 1, 5, 9, 8]
[0, 4, 5, 9, 8]
到结点9的最短路径2条：
[0, 1, 5, 9]
[0, 4, 5, 9]
到结点10的最短路径2条：
[0, 1, 5, 9, 10]
[0, 4, 5, 9, 10]
到结点11的最短路径2条：
[0, 1, 5, 9, 10, 11]
[0, 4, 5, 9, 10, 11]
到结点12的最短路径4条：
[0, 1, 5, 9, 8, 12]
[0, 4, 5, 9, 8, 12]
[0, 1, 5, 9, 13, 12]
[0, 4, 5, 9, 13, 12]
到结点13的最短路径2条：
[0, 1, 5, 9, 13]
[0, 4, 5, 9, 13]
到结点14的最短路径4条：
[0, 1, 5, 9, 10, 14]
[0, 4, 5, 9, 10, 14]
[0, 1, 5, 9, 13, 14]
[0, 4, 5, 9, 13, 14]
到结点15的最短路径6条：
[0, 1, 5, 9, 10, 11, 15]
[0, 4, 5, 9, 10, 11, 15]
[0, 1, 5, 9, 10, 14, 15]
[0, 4, 5, 9, 10, 14, 15]
[0, 1, 5, 9, 13, 14, 15]
[0, 4, 5, 9, 13, 14, 15]