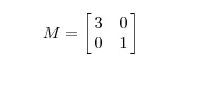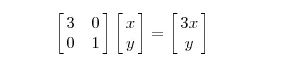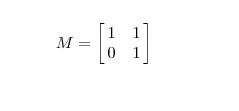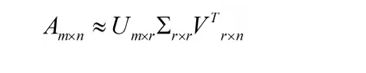- 导致格式错误的 Lambda 代理响应的原因以及如何修复它
zqhdz米时空
汇编
当人们尝试使用AWSAPIGateway和AWSLambda构建无服务器应用程序时,经常出现的一个问题是_由于配置错误而执行失败:Lambda代理响应格式错误。_没有什么比通用错误消息更糟糕的了,它们不会告诉您解决问题所需的任何内容,对吧?AWS并不是以其错误消息设计而闻名,如果甚至可以这样称呼它的话,更不用说为您提供解决问题的方法了。那么如何修复这个Lambda错误以及是什么原因造成的呢?花椒壳
- ROS yaml参数文件的使用
Sun Shiteng
ROS
举个例子,若在params.yaml文件中定义如下参数LidarImageFusion:points_src:"/hilbert_h/deskew/cloud_info"image_src:"/usb_cam0/image_raw"camera_info_src:"/home/hdj/fusion_slam/Color_SLAM_ws/src/hilbert_h/config/firefly_8s
- xwiki html和css,MediaWiki vs. XWiki
Ake阿科
多语言信息技术编程数据库操作系统
140Afar,Abkhazian,Afrikaans,Amharic,Arabic,Assamese,Aymara,Azerbaijani,Bashkir,Byelorussian,Bulgarian,Bihari,Bislama,Bengali;Bangla,Tibetan,Breton,Catalan,Corsican,Czech,Welsh,Danish,German,Bhutani,Gr
- 2021-07-07
潇洒二爷
一辆特斯拉“花格子S型”小车,突然起火,电子技术的车门也失灵TeslaModelSPlaidbrokeintofirewithfailureofelctronicdoors一辆“花格子牌”(ModelSPlaid)特斯拉轿车,在6月29日这天,车主正在路上行驶,突然烈焰腾飞,他的代理律师说,他被短时间困在车内,因为几个电动门都打不开。事情在几天前发生于费城外,这名男子拿到这款特斯拉之后,号称是世界
- 力扣刷题记录(一)剑指Offer(第二版)
乘凉~
求职过程记录leetcode链表算法
1、本栏用来记录社招找工作过程中的内容,包括基础知识学习以及面试问题的记录等,以便于后续个人回顾学习;暂时只有2023年3月份,第一次社招找工作的过程;2、个人经历:研究生期间课题是SLAM在无人机上的应用,有接触SLAM、Linux、ROS、C/C++、DJIOSDK等;3、参加工作后(2021-2023年)岗位是嵌入式软件开发,主要是服务器开发,Linux、C/C++、网络编程、docker容
- 论文笔记—NDT-Transformer: Large-Scale 3D Point Cloud Localization using the Normal Distribution Transfor
入门打工人
笔记slam定位算法
论文笔记—NDT-Transformer:Large-Scale3DPointCloudLocalizationusingtheNormalDistributionTransformRepresentation文章摘要~~~~~~~在GPS挑战的环境中,自动驾驶对基于3D点云的地点识别有很高的要求,并且是基于激光雷达的SLAM系统的重要组成部分(即闭环检测)。本文提出了一种名为NDT-Transf
- 深度学习特征提取魔改版太强了!发文香饽饽!
深度之眼
深度学习干货人工智能干货人工智能深度学习机器学习论文特征提取
要说CV领域经久不衰的研究热点,特征提取可以占一席,毕竟SLAM、三维重建等重要应用的底层都离不开它。再加上近几年深度学习兴起,用深度学习做特征提取逐渐成了主流,比传统算法无论是性能、准确性还是效率都更胜一筹。目前比较常见的深度学习特征提取方法有基于transformer、基于CNN、基于LSTM以及基于GAN,都发展的比较成熟。但为了追求更快速、准确、鲁棒的特征点提取,研究者们开始致力于改进深度
- 视觉SLAM十四讲学习笔记——第十讲 后端优化(2)
晒月光12138
视觉SLAM十四讲学习笔记slamubuntu
上文提到考虑全局的后端优化计算量非常大,因此在计算增量方程时,借助H矩阵的稀疏性加速运算。但是随着时间的推移,累积的相机位姿和路标数量还是会导致计算量过大,以上一节的示例代码数据为例:16张图像,共提取到22106个特征点,这些特征点共出现了83718次。对于一个20Hz更新速度,上述的数据量甚至还不到1s的内容,因此在求解大规模定位建图问题时,一定要控制BA的规模。这里主要有两种解决思路:(1)
- 《Java基础知识》Java Lambda表达式
Limingmingaa
javajava开发语言蓝桥杯
接触Lambda表达式的时候,第一感觉就是,这个是啥?我居然看不懂,于是开始寻找资料,必须弄懂它。先来看一个案例:@FunctionalInterfacepublicinterfaceMyLamda{voidtest1(Stringy);}importdemo.knowledgepoints.Lambda.inf.MyLamda;publicclassLambdaTest{publicsta
- NDT算法
Joeybee
SLAM算法
上一次我们学习了高翔《自动驾驶与机器人中的SLAM技术》中的三维ICP算法,其中包括点对点、点对线、点对面的ICP算法,本次博客学习NDT算法的源码。NDT算法与ICP算法的最大不同之处,在我看来是NDT考虑了均值和方差这两个局部统计量。从最后的求解方法来看,NDT采用了加权最小二乘问题的高斯-牛顿法,和ICP算法的最明显区别是多了权重分布。从高翔书中的测试结果来看,NDT的收敛速度稍弱于点对面I
- SLAM中常用的库
wq_151
人工智能SLAM计算机视觉人工智能机器学习slam
SLAM中常用的库关于库关于库Pangolin是一个用于OpenGL显示/交互以及视频输入的一个轻量级、快速开发库,下面是Pangolin的Github网址:githubEigen是一个高层次的C++库,有效支持线性代数,矩阵和矢量运算,数值分析及其相关的算法。pagenanoflann是一个c++11标准库,用于构建具有不同拓扑(R2,R3(点云),SO(2)和SO(3)(2D和3D旋转组))的
- 【XR】优化SLAM SDK的稳定性
大江东去浪淘尽千古风流人物
xr
优化SLAMSDK的稳定性是确保增强现实(AR)和虚拟现实(VR)应用在各种环境和设备上都能稳定运行的关键。以下是一些主要的优化方法:1.传感器融合优化方法:将多个传感器的数据(如摄像头、加速度计、陀螺仪、磁力计)进行融合,以补偿单一传感器可能存在的误差。优势:提高了环境理解的准确性,减少了由于单一传感器误差导致的抖动和漂移现象。实例:ARKit和ARCore都利用了传感器融合技术来增强稳定性。2
- ROS2导航SLAM建图探索
鱼香ROS
ROS2机器人SLAMROS2导航SLAM
大家好,我是昨晚熬夜太多脑壳痛的小鱼。今天带大家一起探索一些ROS2+turtlebot3的slam建图。先上最终效果图1.安装ROS2第一步就是要有一个ROS2的环境,这个没有的请打开小鱼的fishros网站,选择一行代码安装ROS2进行安装。2.安装turtlebot3sudoaptinstallros-foxy-turtlebot3*sudoaptinstallros-foxy-cartog
- 数百倍加速!港科大最新:嵌入式平台上实时运行的NeRF SLAM!
计算机视觉工坊
3D视觉从入门到精通学习自动驾驶算法
来源:计算机视觉工坊添加微信:dddvision,备注:NeRF,拉你入群。文末附行业细分群0.笔者个人体会传统的NeRF和NeRFSLAM所需要的计算量非常大,很难在嵌入式设备上跑起来,这也就很大程度上限制了NeRFSLAM的落地。但最近港科大&中山大学提出了一项工作Photo-SLAM,不仅实现了高保真的建图,还可以在嵌入式设备上实时运行,甚至渲染速度提高了数百倍。下面一起来阅读一下这项工作,
- 自动驾驶-机器人-slam-定位面经和面试知识系列07之C++STL面试题(03)
lonely-stone
面试c++职场和发展
这个博客系列会分为C++STL-面经、常考公式推导和SLAM面经面试题等三个系列进行更新,基本涵盖了自己秋招历程被问过的面试内容(除了实习和学校项目相关的具体细节)。在知乎和牛客也会同步更新,全网同号(lonely-stone或者lonely_stone)。关于高频面试题和C++STL面经,每次我会更新10个问题左右,每次更新过多,害怕大家可能看了就只记住其中几个点。(在个人秋招面试过程中,面试到
- 激光SLAM--(8) LeGO-LOAM论文笔记
lonely-stone
slam激光SLAM论文阅读
论文标题:LeGO-LOAM:LightweightandGround-OptimizedLidarOdometryandMappingonVariableTerrain应用在可变地形场景的轻量级的、并利用地面优化的LOAMABSTRACT轻量级的、基于地面优化的LOAM实时进行六自由度位姿估计,应用在地面的车辆上。强调应用在地面车辆上是因为在这里面要求雷达必须水平安装,而像LOAM和LIO-SA
- 自动驾驶-机器人-slam-定位面经和面试知识系列03之C++STL面试题(01)
lonely-stone
面试c++职场和发展
这两天有点忙耽搁了,抱歉!!!这个博客系列会分为C++STL-面经、常考公式推导和SLAM面经面试题等三个系列进行更新,基本涵盖了自己秋招历程被问过的面试内容(除了实习和学校项目相关的具体细节)。在知乎和牛客也会同步更新,全网同号(lonely-stone或者lonely_stone)。关于高频面试题和C++STL面经,每次我会更新10个问题左右,每次更新过多,害怕大家可能看了就只记住其中几个点。
- 自动驾驶-机器人-slam-定位面经和面试知识系列04之高频面试题(02)
lonely-stone
自动驾驶机器人面试
这个博客系列会分为C++STL-面经、常考公式推导和SLAM面经面试题等三个系列进行更新,基本涵盖了自己秋招历程被问过的面试内容(除了实习和学校项目相关的具体细节)。在知乎和牛客也会同步更新,全网同号(lonely-stone或者lonely_stone)。关于高频面试题和C++STL面经,每次我会更新10个问题左右,每次更新过多,害怕大家可能看了就只记住其中几个点。(在个人秋招面试过程中,面试到
- 【自动驾驶】自动驾驶地图构建方法与工具小结
CS_Zero
自动驾驶人工智能
自动驾驶地图构建小结概述制作流程主要利用定位与建图算法(组合导航,视觉、激光SLAM等),融合多种传感器数据,构建高精度、高分辨率的三维语义地图,将要素矢量化,构建要素间的关联关系,通过质检确保质量可靠,形成地图引擎(服务、API)以满足自动驾驶系统的需求。底图构建底图构建存在两大类方法,点云建图与视觉建图。点云建图一般面向高精度采集设备,采用高线束激光雷达,硬件成本高。一般使用高精度组合导航进行
- Android D8 编译器 和 R8 工具,【一篇文章搞懂】
安卓开发top
Androidandroidjavaeclipse移动开发
android.enableIncrementalDesugaring=false.android.enableDesugar=false2.1Lambda表达式Java8中一个重大变更是引入Lambda表达式。publicclassLambda{publicstaticvoidmain(String[]args){logDebug(msg->System.out.println(msg),"He
- 特斯拉神器TeslaMate一键安装,终于来了
oakley0
cartesla云服务器腾讯云
之前分享了teslamate的功能和简单安装方法,很多喜欢尝鲜的车友尝试了,但安装过程对不熟悉linux服务器的非码农来说还是有点小艰辛。趁这回双十一腾讯云重磅优惠,我也重新屯了服务器重装了一遍,现在把简化后安装过程、一键安装方法包括加密登录的方式分享一下。目录1.购买服务器2.登录服务器3.安装TeslaMate3.1切换管理员用户3.2一键安装TeslaMate-【简单模式】3.3一键安装Te
- 特斯拉神器TeslaMate一键安装,来了
oakley04
腾讯云阿里云云计算
之前分享了teslamate的功能和简单安装方法,很多喜欢尝鲜的车友尝试了,但安装过程对不熟悉linux服务器的非码农来说还是有点小艰辛。趁这回双十一腾讯云重磅优惠,我也重新屯了服务器重装了一遍,现在把简化后安装过程或一键安装方法分享一下。1.购买服务器以下三款服务器都可以,其中最推荐中间的2核4G8M带宽的三年198,还没入手请点击下面的入口链接:腾讯云运营活动-腾讯云https://curl.
- TeslaMate特斯拉神器本地Docker部署实现无公网远程访问
nagiY
てんさいdocker容器运维sql
文章目录1.Docker部署TeslaMate2.本地访问TeslaMate3.Linux安装Cpolar4.配置TeslaMate公网地址5.远程访问TeslaMate6.固定TeslaMate公网地址7.固定地址访问TeslaMateTeslaMate是一个开源软件,可以通过连接特斯拉账号,记录行驶历史,统计能耗、里程、充电次数等数据。用户可以通过web界面查看车辆状态、行程报告、充电记录等信
- Ubuntu环境搭建TeslaMate,特斯拉车友必备,可视化数据仪表!使用极空间Z4虚拟机
喵不是白养的
ubuntulinux
能点进来的大概率都是特斯拉车友~~本篇记录一下使用极空间Z4家庭NAS搭建TeslaMate的全过程,使用极空间最近更新的虚拟机功能,在虚拟机中安装Ubuntu部署Docker。当然大家用PC虚拟机搭建也可以啦!至于为什么不用极空间自带的Docker功能,emmm并不好用。要是想要使用自带的docker来搭建,可以参照这个https://post.smzdm.com/p/az59px95/本人自学
- 使用Docker部署TeslaMate并结合内网穿透软件实现远程访问车辆数据
比奥利奥还傲.
docker容器运维服务器linux
文章目录1.Docker部署TeslaMate2.本地访问TeslaMate3.Linux安装Cpolar4.配置TeslaMate公网地址5.远程访问TeslaMate6.固定TeslaMate公网地址7.固定地址访问TeslaMateTeslaMate是一个开源软件,可以通过连接特斯拉账号,记录行驶历史,统计能耗、里程、充电次数等数据。用户可以通过web界面查看车辆状态、行程报告、充电记录等信
- 如何在本地服务器部署TeslaMate并远程查看特斯拉汽车数据无需公网ip
日出等日落
内网穿透服务器汽车tcp/ip
文章目录1.Docker部署TeslaMate2.本地访问TeslaMate3.Linux安装Cpolar4.配置TeslaMate公网地址5.远程访问TeslaMate6.固定TeslaMate公网地址7.固定地址访问TeslaMateTeslaMate是一个开源软件,可以通过连接特斯拉账号,记录行驶历史,统计能耗、里程、充电次数等数据。用户可以通过web界面查看车辆状态、行程报告、充电记录等信
- 伊朗藏红花前五个月出口增长33%
西域竹君斋
Iran’ssaffronexportsincreased33percentduringthefirstfivemonthsofthecurrentIraniancalendaryear(March21-August22)comparedtothesameperiodoftimeinthepastyear,accordingtothelatestdatareleasedbytheIslamicRe
- 如何实现基于图像与激光雷达的 3d 场景重建?
大势智慧
3d人工智能计算机视觉三维建模激光点云
智影S100是一款基于图像和激光点云融合建模技术的高精度轻巧手持SLAM三维激光扫描仪。设备机身小巧、手持轻便,可快速采集点云数据;支持实时解算、实时预览点云成果,大幅提高内外业工作效率;同时支持一键生成实景三维Mesh模型,实现城市建筑、堆体、室内空间等场景的高逼真3d重建。以下是智影S100在国家游泳中心“水立方”进行实地采集的点云与模型成果展示:智影S100:水立方立面点云与模型成果分享,实
- ROS目标跟随(路径规划、雷达、slam、定位)
海风-
ROS小车跟随目标跟随雷达路径规划定位
ROS目标跟随(路径规划、雷达、地图、定位)最终效果展示一、总体launch文件1、打开已有地图2、组合小车的各个部分2.1惯性矩阵设置2.2小车底盘2.3摄像头2.4雷达2.5为机器人模型添加传动装置以及控制器2.6为机器人模型添加雷达配置2.7为机器人模型添加摄像头配置2.8为机器人模型添加kinect摄像头配置3、定位系统(amcl)4、路径规划(move_base)4.1全局路径规划与本地
- ROS小车跟随
海风-
ROS小车跟随目标跟随雷达
这篇的目的是方便自己复习总体流程1、gazebo仿真世界2、机器人模型3、slam建图4、定位5、路径规划6、小车跟随7、总体launch文件第一篇博客给出了总体代码:https://blog.csdn.net/m0_71523511/article/details/135610191第二篇博客改善了跟随的效果:https://blog.csdn.net/m0_71523511/article/d
- 对于规范和实现,你会混淆吗?
yangshangchuan
HotSpot
昨晚和朋友聊天,喝了点咖啡,由于我经常喝茶,很长时间没喝咖啡了,所以失眠了,于是起床读JVM规范,读完后在朋友圈发了一条信息:
JVM Run-Time Data Areas:The Java Virtual Machine defines various run-time data areas that are used during execution of a program. So
- android 网络
百合不是茶
网络
android的网络编程和java的一样没什么好分析的都是一些死的照着写就可以了,所以记录下来 方便查找 , 服务器使用的是TomCat
服务器代码; servlet的使用需要在xml中注册
package servlet;
import java.io.IOException;
import java.util.Arr
- [读书笔记]读法拉第传
comsci
读书笔记
1831年的时候,一年可以赚到1000英镑的人..应该很少的...
要成为一个科学家,没有足够的资金支持,很多实验都无法完成
但是当钱赚够了以后....就不能够一直在商业和市场中徘徊......
- 随机数的产生
沐刃青蛟
随机数
c++中阐述随机数的方法有两种:
一是产生假随机数(不管操作多少次,所产生的数都不会改变)
这类随机数是使用了默认的种子值产生的,所以每次都是一样的。
//默认种子
for (int i = 0; i < 5; i++)
{
cout<<
- PHP检测函数所在的文件名
IT独行者
PHP函数
很简单的功能,用到PHP中的反射机制,具体使用的是ReflectionFunction类,可以获取指定函数所在PHP脚本中的具体位置。 创建引用脚本。
代码:
[php]
view plain
copy
// Filename: functions.php
<?php&nbs
- 银行各系统功能简介
文强chu
金融
银行各系统功能简介 业务系统 核心业务系统 业务功能包括:总账管理、卡系统管理、客户信息管理、额度控管、存款、贷款、资金业务、国际结算、支付结算、对外接口等 清分清算系统 以清算日期为准,将账务类交易、非账务类交易的手续费、代理费、网络服务费等相关费用,按费用类型计算应收、应付金额,经过清算人员确认后上送核心系统完成结算的过程 国际结算系
- Python学习1(pip django 安装以及第一个project)
小桔子
pythondjangopip
最近开始学习python,要安装个pip的工具。听说这个工具很强大,安装了它,在安装第三方工具的话so easy!然后也下载了,按照别人给的教程开始安装,奶奶的怎么也安装不上!
第一步:官方下载pip-1.5.6.tar.gz, https://pypi.python.org/pypi/pip easy!
第二部:解压这个压缩文件,会看到一个setup.p
- php 数组
aichenglong
PHP排序数组循环多维数组
1 php中的创建数组
$product = array('tires','oil','spark');//array()实际上是语言结构而不 是函数
2 如果需要创建一个升序的排列的数字保存在一个数组中,可以使用range()函数来自动创建数组
$numbers=range(1,10)//1 2 3 4 5 6 7 8 9 10
$numbers=range(1,10,
- 安装python2.7
AILIKES
python
安装python2.7
1、下载可从 http://www.python.org/进行下载#wget https://www.python.org/ftp/python/2.7.10/Python-2.7.10.tgz
2、复制解压
#mkdir -p /opt/usr/python
#cp /opt/soft/Python-2
- java异常的处理探讨
百合不是茶
JAVA异常
//java异常
/*
1,了解java 中的异常处理机制,有三种操作
a,声明异常
b,抛出异常
c,捕获异常
2,学会使用try-catch-finally来处理异常
3,学会如何声明异常和抛出异常
4,学会创建自己的异常
*/
//2,学会使用try-catch-finally来处理异常
- getElementsByName实例
bijian1013
element
实例1:
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/1999/x
- 探索JUnit4扩展:Runner
bijian1013
java单元测试JUnit
参加敏捷培训时,教练提到Junit4的Runner和Rule,于是特上网查一下,发现很多都讲的太理论,或者是举的例子实在是太牵强。多搜索了几下,搜索到两篇我觉得写的非常好的文章。
文章地址:http://www.blogjava.net/jiangshachina/archive/20
- [MongoDB学习笔记二]MongoDB副本集
bit1129
mongodb
1. 副本集的特性
1)一台主服务器(Primary),多台从服务器(Secondary)
2)Primary挂了之后,从服务器自动完成从它们之中选举一台服务器作为主服务器,继续工作,这就解决了单点故障,因此,在这种情况下,MongoDB集群能够继续工作
3)挂了的主服务器恢复到集群中只能以Secondary服务器的角色加入进来
2
- 【Spark八十一】Hive in the spark assembly
bit1129
assembly
Spark SQL supports most commonly used features of HiveQL. However, different HiveQL statements are executed in different manners:
1. DDL statements (e.g. CREATE TABLE, DROP TABLE, etc.)
- Nginx问题定位之监控进程异常退出
ronin47
nginx在运行过程中是否稳定,是否有异常退出过?这里总结几项平时会用到的小技巧。
1. 在error.log中查看是否有signal项,如果有,看看signal是多少。
比如,这是一个异常退出的情况:
$grep signal error.log
2012/12/24 16:39:56 [alert] 13661#0: worker process 13666 exited on s
- No grammar constraints (DTD or XML schema).....两种解决方法
byalias
xml
方法一:常用方法 关闭XML验证
工具栏:windows => preferences => xml => xml files => validation => Indicate when no grammar is specified:选择Ignore即可。
方法二:(个人推荐)
添加 内容如下
<?xml version=
- Netty源码学习-DefaultChannelPipeline
bylijinnan
netty
package com.ljn.channel;
/**
* ChannelPipeline采用的是Intercepting Filter 模式
* 但由于用到两个双向链表和内部类,这个模式看起来不是那么明显,需要仔细查看调用过程才发现
*
* 下面对ChannelPipeline作一个模拟,只模拟关键代码:
*/
public class Pipeline {
- MYSQL数据库常用备份及恢复语句
chicony
mysql
备份MySQL数据库的命令,可以加选不同的参数选项来实现不同格式的要求。
mysqldump -h主机 -u用户名 -p密码 数据库名 > 文件
备份MySQL数据库为带删除表的格式,能够让该备份覆盖已有数据库而不需要手动删除原有数据库。
mysqldump -–add-drop-table -uusername -ppassword databasename > ba
- 小白谈谈云计算--基于Google三大论文
CrazyMizzz
Google云计算GFS
之前在没有接触到云计算之前,只是对云计算有一点点模糊的概念,觉得这是一个很高大上的东西,似乎离我们大一的还很远。后来有机会上了一节云计算的普及课程吧,并且在之前的一周里拜读了谷歌三大论文。不敢说理解,至少囫囵吞枣啃下了一大堆看不明白的理论。现在就简单聊聊我对于云计算的了解。
我先说说GFS
&n
- hadoop 平衡空间设置方法
daizj
hadoopbalancer
在hdfs-site.xml中增加设置balance的带宽,默认只有1M:
<property>
<name>dfs.balance.bandwidthPerSec</name>
<value>10485760</value>
<description&g
- Eclipse程序员要掌握的常用快捷键
dcj3sjt126com
编程
判断一个人的编程水平,就看他用键盘多,还是鼠标多。用键盘一是为了输入代码(当然了,也包括注释),再有就是熟练使用快捷键。 曾有人在豆瓣评
《卓有成效的程序员》:“人有多大懒,才有多大闲”。之前我整理了一个
程序员图书列表,目的也就是通过读书,让程序员变懒。 程序员作为特殊的群体,有的人可以这么懒,懒到事情都交给机器去做,而有的人又可以那么勤奋,每天都孜孜不倦得
- Android学习之路
dcj3sjt126com
Android学习
转自:http://blog.csdn.net/ryantang03/article/details/6901459
以前有J2EE基础,接触JAVA也有两三年的时间了,上手Android并不困难,思维上稍微转变一下就可以很快适应。以前做的都是WEB项目,现今体验移动终端项目,让我越来越觉得移动互联网应用是未来的主宰。
下面说说我学习Android的感受,我学Android首先是看MARS的视
- java 遍历Map的四种方法
eksliang
javaHashMapjava 遍历Map的四种方法
转载请出自出处:
http://eksliang.iteye.com/blog/2059996
package com.ickes;
import java.util.HashMap;
import java.util.Iterator;
import java.util.Map;
import java.util.Map.Entry;
/**
* 遍历Map的四种方式
- 【精典】数据库相关相关
gengzg
数据库
package C3P0;
import java.sql.Connection;
import java.sql.SQLException;
import java.beans.PropertyVetoException;
import com.mchange.v2.c3p0.ComboPooledDataSource;
public class DBPool{
- 自动补全
huyana_town
自动补全
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd"><html xmlns="http://www.w3.org/1999/xhtml&quo
- jquery在线预览PDF文件,打开PDF文件
天梯梦
jquery
最主要的是使用到了一个jquery的插件jquery.media.js,使用这个插件就很容易实现了。
核心代码
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.
- ViewPager刷新单个页面的方法
lovelease
androidviewpagertag刷新
使用ViewPager做滑动切换图片的效果时,如果图片是从网络下载的,那么再子线程中下载完图片时我们会使用handler通知UI线程,然后UI线程就可以调用mViewPager.getAdapter().notifyDataSetChanged()进行页面的刷新,但是viewpager不同于listview,你会发现单纯的调用notifyDataSetChanged()并不能刷新页面
- 利用按位取反(~)从复合枚举值里清除枚举值
草料场
enum
以 C# 中的 System.Drawing.FontStyle 为例。
如果需要同时有多种效果,
如:“粗体”和“下划线”的效果,可以用按位或(|)
FontStyle style = FontStyle.Bold | FontStyle.Underline;
如果需要去除 style 里的某一种效果,
- Linux系统新手学习的11点建议
刘星宇
编程工作linux脚本
随着Linux应用的扩展许多朋友开始接触Linux,根据学习Windwos的经验往往有一些茫然的感觉:不知从何处开始学起。这里介绍学习Linux的一些建议。
一、从基础开始:常常有些朋友在Linux论坛问一些问题,不过,其中大多数的问题都是很基础的。例如:为什么我使用一个命令的时候,系统告诉我找不到该目录,我要如何限制使用者的权限等问题,这些问题其实都不是很难的,只要了解了 Linu
- hibernate dao层应用之HibernateDaoSupport二次封装
wangzhezichuan
DAOHibernate
/**
* <p>方法描述:sql语句查询 返回List<Class> </p>
* <p>方法备注: Class 只能是自定义类 </p>
* @param calzz
* @param sql
* @return
* <p>创建人:王川</p>
* <p>创建时间:Jul
![]()
![]() )
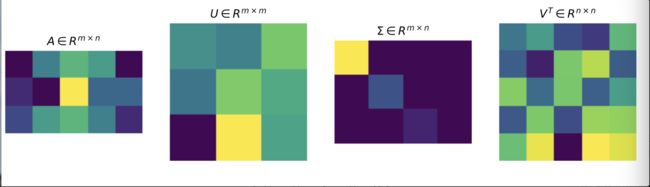
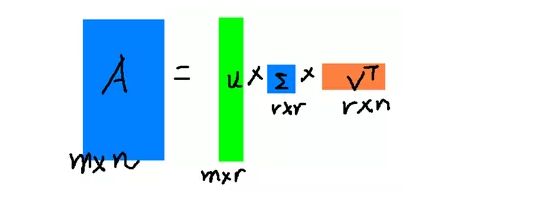
)![]() 是一个N * N的矩阵,里面的向量也是正交的,V里面的向量称为右奇异向量且为单位正交阵
是一个N * N的矩阵,里面的向量也是正交的,V里面的向量称为右奇异向量且为单位正交阵![]() ),从图片来反映几个相乘的矩阵的大小可得下面的图片:
),从图片来反映几个相乘的矩阵的大小可得下面的图片:![]() 或者
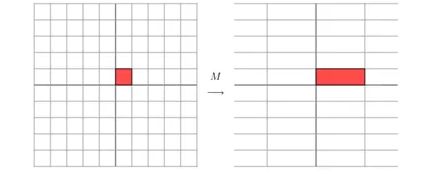
或者 ![]()
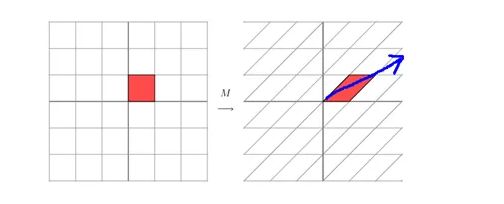
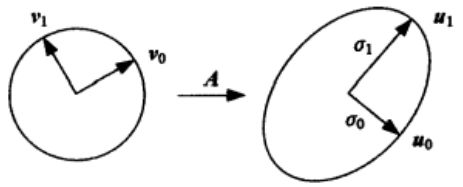
![]() 时,会把
时,会把![]() 变换到
变换到![]() 的方向,同时将的长度
的方向,同时将的长度![]() 变成
变成![]() 。也可以看成先旋转然后缩放再旋转的过程。
。也可以看成先旋转然后缩放再旋转的过程。