「CF1194E」Count The Rectangles【树状数组】

E. Count The Rectangles

time limit per test 2 seconds memory limit per test 256 megabytes input standard input output standard output

There are $n$ segments drawn on a plane; the $i-th$ segment connects two points $(x_{i1},y_{i,1})$ and $(x_{i,2},y_{i,2})$. Each segment is non-degenerate, and is either horizontal or vertical — formally, for every ?∈[1,?] either $x_{i,1}=x_{i,2}$ or $y_{i,1}=y_{i,2}$ (but only one of these conditions holds). Only segments of different types may intersect: no pair of horizontal segments shares any common points, and no pair of vertical segments shares any common points.

We say that four segments having indices $h_1,h_2,v_{1}and{v}_2$ such that $h_1<h_2$ and $v_1<v_2$ form a rectangle if the following conditions hold:

segments $h_1$ and $h_2$ are horizontal;
segments $v_1$ and $v_2$ are vertical;
segment $h_1$ intersects with segment $v_1$;
segment $h_2$ intersects with segment $v_1$;
segment $h_1$ intersects with segment $v_2$;
segment $h_2$ intersects with segment $v_2$.
Please calculate the number of ways to choose four segments so they form a rectangle. Note that the conditions $h_1<h_2$ and $v_1<v_2$ should hold.

Input

The first line contains one integer $n(1\le n\le 5000)$ — the number of segments.

Then $n$ lines follow. The $i-th$ line contains four integers $x_{i,1},y_{i,1},x_{i,2}$ and $y_{i,2}$ denoting the endpoints of the $i-th$ segment. All coordinates of the endpoints are in the range $[-5000,5000]$.

It is guaranteed that each segment is non-degenerate and is either horizontal or vertical. Furthermore, if two segments share a common point, one of these segments is horizontal, and another one is vertical.

Output

Print one integer — the number of ways to choose four segments so they form a rectangle.

Examples

input

7
-1 4 -1 -2
6 -1 -2 -1
-2 3 6 3
2 -2 2 4
4 -1 4 3
5 3 5 1
5 2 1 2

output

7

input

5
1 5 1 0
0 1 5 1
5 4 0 4
4 2 4 0
4 3 4 5

output

0

Note

The following pictures represent sample cases:

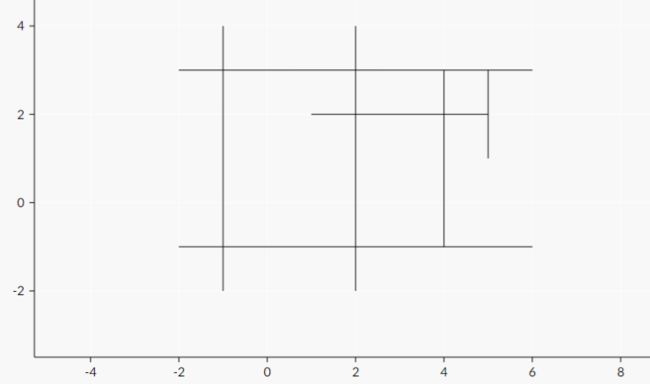
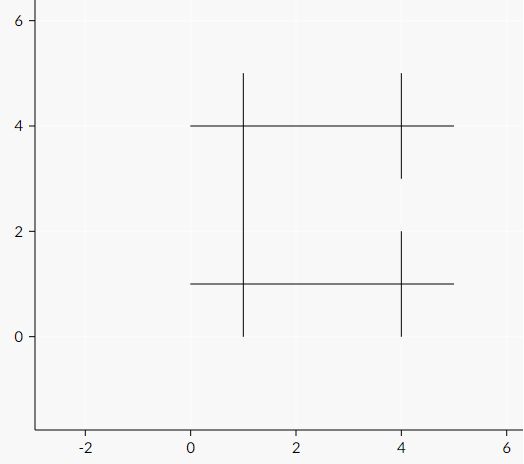
题意

• 给你$n$条平行于$x$轴或者$y$轴的直线，求能构成多少个不同的矩形

题解

• 暴力用树状数组维护一下就行了

代码

#include
 
using namespace std;
const int maxn=5005;
const int maxl=1e4+2;
int n;
vector<pair<int,int> >hor[maxl],ver[maxl];
vector<int> cur[maxl];
 
struct node{
	int sum[maxl];
	int lowbit(int x) {return x&(-x);} 
	void add(int id,int val){
		for(int i=id;i<maxl;i+=lowbit(i)){
			sum[i]+=val;
		}
	}
	
	int query(int id){
		int ans=0;
		for(int i=id;i>=1;i-=lowbit(i)){
			ans+=sum[i];
		}
		return ans;
	}
 
	int s(int l,int r){
		return query(r)-query(l-1);
	}
	
	void clear(){memset(sum,0,sizeof(sum));}
}bit;
 
int main()
{
	scanf("%d",&n);
	for(int i=1,x1,x2,y1,y2;i<=n;i++){
		scanf("%d %d %d %d",&x1,&y1,&x2,&y2);
		x1+=5001;x2+=5001;y1+=5001;y2+=5001;
		if(y1==y2) hor[y1].push_back(make_pair(min(x1,x2),max(x1,x2)));
		else ver[x1].push_back(make_pair(min(y1,y2),max(y1,y2)));
	}
	long long ans=0;
	for(int i=1;i<maxl;i++) {
		for(auto h1:hor[i]) {
			bit.clear();
			for(int j=1;j<maxl;j++) cur[j].clear();
			for(int j=h1.first;j<=h1.second;j++){
				for(auto v:ver[j]){
					if(v.first<=i&&v.second>i){
						cur[v.second].push_back(j);
						bit.add(j,1);
					}
				}
			}
			for(int y2=i+1;y2<maxl;y2++){
				for(auto h2:hor[y2]) {
					int res=bit.s(h2.first,h2.second);
					ans+=1LL*res*(res-1)/2;
				}
				for(auto j:cur[y2]) bit.add(j,-1);
			}
 
		}
	}
	printf("%lld\n",ans);
}