BZOJ 2038 && hdu 6333
2038: [2009国家集训队]小Z的袜子(hose)
Time Limit: 20 Sec Memory Limit: 259 MB
Submit: 15491 Solved: 7029
[Submit][Status][Discuss]
Description
作为一个生活散漫的人,小Z每天早上都要耗费很久从一堆五颜六色的袜子中找出一双来穿。终于有一天,小Z再也无法忍受这恼人的找袜子过程,于是他决定听天由命……
具体来说,小Z把这N只袜子从1到N编号,然后从编号L到R(L 尽管小Z并不在意两只袜子是不是完整的一双,甚至不在意两只袜子是否一左一右,他却很在意袜子的颜色,毕竟穿两只不同色的袜子会很尴尬。
你的任务便是告诉小Z,他有多大的概率抽到两只颜色相同的袜子。当然,小Z希望这个概率尽量高,所以他可能会询问多个(L,R)以方便自己选择。
Input
输入文件第一行包含两个正整数N和M。N为袜子的数量,M为小Z所提的询问的数量。接下来一行包含N个正整数Ci,其中Ci表示第i只袜子的颜色,相同的颜色用相同的数字表示。再接下来M行,每行两个正整数L,R表示一个询问。
Output
包含M行,对于每个询问在一行中输出分数A/B表示从该询问的区间[L,R]中随机抽出两只袜子颜色相同的概率。若该概率为0则输出0/1,否则输出的A/B必须为最简分数。(详见样例)
sol: 莫队模板题,记录一下
code:
/**************************************************************
Problem: 2038
User: SSCTTSQQ
Language: C++
Result: Accepted
Time:1364 ms
Memory:24272 kb
****************************************************************/
#include
#include
#include
using namespace std;
typedef long long ll;
const int maxn = 5e5+10;
#define fi first
#define se second
int c[maxn],pos[maxn],cnt[maxn];
pair sol[maxn];
ll gcd(ll a,ll b){
return b==0?a:gcd(b,a%b);
}
struct Query{
int l,r;
int id;
ll val;
bool operator <(const Query& s) const{
return pos[l]==pos[s.l]? rq[i].l) {l--; add(c[l],ret);}
while(rq[i].r) {del(c[r],ret); r--;}
q[i].val = ret;
}
for(int i=1;i<=m;i++){
ll a = q[i].val - (q[i].r-q[i].l+1);
ll b = (ll)(q[i].r - q[i].l)*(q[i].r-q[i].l+1);
if(a==0){
sol[q[i].id].fi = 0;
sol[q[i].id].se = 1;
continue;
}
ll g = gcd(a,b);
a/=g;
b/=g;
sol[q[i].id].fi = a;
sol[q[i].id].se = b;
}
for(int i=1;i<=m;i++){
printf("%lld/%lld\n",sol[i].fi,sol[i].se);
}
return 0;
}
hdu 6333:
Problem B. Harvest of Apples
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 262144/262144 K (Java/Others)
Total Submission(s): 837 Accepted Submission(s): 304
Problem Description
There are n apples on a tree, numbered from 1 to n.
Count the number of ways to pick at most m apples.
Input
The first line of the input contains an integer T (1≤T≤105) denoting the number of test cases.
Each test case consists of one line with two integers n,m (1≤m≤n≤105).
Output
For each test case, print an integer representing the number of ways modulo 109+7.
Sample Input
2 5 2 1000 500
Sample Output
16 924129523
Source
2018 Multi-University Training Contest 4
sol:
由生成函数可得  。看到范围就觉得是莫队,xjb笔画了下发现
。看到范围就觉得是莫队,xjb笔画了下发现![]() 向
向 ![]() 转化和m有关,
转化和m有关,以为前缀和不可做弃疗。
考虑![]() ,则有
,则有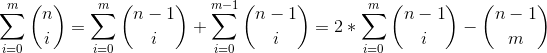 。设
。设 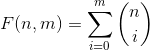 ,则有
,则有![]() ,
,![]() 。预处理阶乘后可在O(1)时间内完成区间加减,莫队处理即可。
。预处理阶乘后可在O(1)时间内完成区间加减,莫队处理即可。
code:
#include
using namespace std;
typedef long long ll;
const int maxn = 1e5+50;
const int mod = 1000000007;
ll fac[maxn],inv[maxn],ans[maxn];
int pos[maxn];
ll Pow(ll a, ll b) {
ll sum = 1;
while (b) {
if (b & 1) sum = sum*a%mod;
a = a*a%mod;
b >>= 1;
}
return sum;
}
inline ll Inv(int n) {
return Pow(n, mod - 2);
}
void init(int n) {
fac[0] = fac[1] = inv[0] = inv[1] = 1;
for (int i = 2; i <= n; i++) fac[i] = fac[i - 1] * i%mod;
inv[n] = Inv(fac[n]);
for (int i = n - 1; i>1; i--) inv[i] = inv[i + 1] * (i + 1) % mod;
}
inline ll C(int n, int m) {
return fac[n] * inv[n - m] % mod*inv[m] % mod;
}
struct query{
int id,m,n;
bool operator <(const query& s){
return pos[m]==pos[s.m]?n=mod) x-=mod;
}
void Mul(ll& x,ll y){
x = x*y;
if(x>=mod) x%=mod;
}
void Sub(ll& x,ll y){
x = x+mod-y;
if(x>=mod) x-=mod;
}
int main(){
init(maxn-1);
int T;
scanf("%d",&T);
int sq = sqrt(1e5);
ll di2 = Inv(2);
for(int i = 1;iq[i].m){
Sub(ret,C(r,l));
l--;
}
while(lq[i].n){
r--;
Add(ret,C(r,l));
Mul(ret,di2);
}
ans[q[i].id] = ret;
}
for(int i=1;i<=T;i++){
printf("%lld\n",ans[i]);
}
return 0;
}