Java 哈希函数 哈希表 动态容量 链地址法 简介+实现
- 简介
- 哈希函数
- 整型
- 浮点型
- 字符串型
- Java 中的hashCode()
- 哈希冲突
- 时间复杂度
- 动态空间处理
- 适用范围
- 实现
简介
实现哈希表有两个主要的问题, 一个是解决哈希函数的设计, 一个是哈希冲突的处理
哈希函数
键通过哈希函数可以得到一个索引, 通过索引可以在内存中找到这个键所包含的信息, 索引的分布越均匀冲突才越少
所有类型的数据, 包括浮点型, 字符型的都可以转化为整型, 然后用整型的哈希函数计算
哈希函数的设计要遵循一些原则:
- 一致性: 如果 a == b, 则 hash(a) == hash(b)
- 高效性: 计算高效简便
- 均匀性: 哈希值均匀分布
整型
如果是小范围正整数, 可以直接把键作为索引使用, 比如字母表的大小只有26, 1对应a, 2对应b…
如果是小范围的负整数, 可以加偏移, -10 ~ 10 偏移10的话就转为 0 ~ 20
如果是大整数, 如身份证号, 通常是取模, 比如身份证号码401625198906031289, 如果mod 1000000的话, 也就是取后6位, 会有一个问题, 那就是日期的范围不是00~99, 会导致分布不均匀,
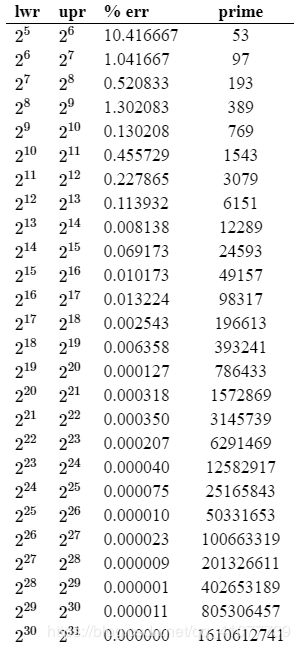
最简单的解决方法是模一个素数, 可以根据你的数据范围, 到 这里 查找合适的素数 (模素数可以更均匀地分布)
浮点型
把存储浮点数的32位或者64位二进制当作整型处理
字符串型
比如 love = l * 26^3 + o * 26^2 + v * 26^1 + e * 26^0, 当作26进制的数字, 如果字符串不止有小写字母, 还有字符串, 大写字母的话, 也可以修改26, 下面用 B表示, 如果M表示素数的话, love的哈希值是
hash(love)
= (l * B^3 + o * B^2 + v * B^1 + e * B^0)%M
= ((((l * B) + o * B) + v * B) + e * B) % M
= ((((l % M) * B + o) % M * B + v) % M * B + e) % M. . . . . .每次都先模一次M可以防止整型溢出
代码如下
int hash = 0;
for(int i=0; i<s.length(); i++)
hash = (hash * B + s.charAt(i)) % M
Java 中的hashCode()
将浮点型, 字符串型等非整型的转化为整型
int a = 35;
System.out.println(((Integer)a).hashCode());
运行结果: 35
int a2 = 35;
System.out.println(((Integer)a2).hashCode());
运行结果: 35 // 输入一样, 输出一样
int b = -35;
System.out.println(((Integer)b).hashCode());
运行结果: -35
double c = 3.14159265;
System.out.println(((Double)c).hashCode());
运行结果: 331478282
String d = "To freedom";
System.out.println(d.hashCode());
运行结果: 1240310481
因为Java并不知道我们的数据规模, 所以不知道要模多大的素数, hashCode()得到的不是索引, 得模完素数之后才得到索引
Object类默认都是有 hashCode() 这个方法的, 所有类都是Object类的子类, 这也是为什么上面的int, double要转化为Integer类, Double类.
如果是自己定义的类, 通常是要 重写hashCode() 的, 因为没有重写hashCode()的话, 那么用的就是Object类中的hashCode(), 这个方法把对象的地址映射成整型, 所以只要地址不同, hashCode()返回的值就会不同, 这通常都不是我们想要的
除此之外, 通常还要 重写equal() , 用于在哈希冲突的时候判断两个对象是不是一样
例子如下
public class Person{
public String name;
public int age;
Person(String name, int age){
this.name = name;
this.age = age;
}
@Override
public int hashCode(){
int B = 31;
int hash = 0;
hash = hash * B + name.hashCode();
hash = hash * B + age;
return hash;
}
@Override
public boolean equals(Object o){
if(this == o)
return true;
if(o == null)
return false;
if(getClass() != o.getClass())
return false;
Person another = (Person)o; // 强制类型转化
return this.name == another.name && this.age == another.age
}
}
哈希冲突
处理方法: 链地址法(Separate Chaining), 开发地址法, 再哈希法, Coalesced Hashing(综合 Separate Chaining 和 开发地址法)
这里只介绍链地址法, 有需要再填坑
有哈希冲突时候, 可以用链表把不同的键值挂在同一索引上, 也可以用树

在Java8之前, 每一个索引位置对应一个链表
在Java8之后, 一开始每一个索引位置依然对应一个链表, 但是当哈希冲突达到一定程度后(比如每一个位置的存储的元素数超过一定数量), Java就会把链表转为红黑树, 也就是TreeMap(底层实现就是红黑树), 因为冲突小的时候, 链表更快, 但是! 转为红黑树有一个条件, 就是哈希表的键要可比较, 因为红黑树是有序的, 可比较才可以排序
时间复杂度
N个元素放入有M个地址的哈希表, 平均每个地址存N/M个元素
如果用的是链表存储, 时间复杂度是 O(N/M)
如果用的是平衡树, 时间复杂度是 O(log(N/M)
动态空间处理
当N无线增大时, 时间复杂度就会很大
所以要达到 O(1), 就要使用动态的哈希表, M要随着N的增大而增大
当每个地址承载的元素多到一定程度时, 扩容: N/M >= upperTol (上界)
if(size >= upperTol * M) // 用除法会有误差, size是存储的元素个数, M是哈希表容量
resize(2 * M); // 扩大为原来的两倍
当每个地址承载的元素少到一定程度时, 缩容: N/M < lowerTol (下界)
if(size < lowerTol * M && M / 2 >= initCapacity) // 要防止缩太小, 不能小于初始容量
resize(M / 2); // 变为原来的一半
设置了两个界限, 可以避免震荡, 如果只有一个界限, 在边界反复添加删除就会导致M反复变化
扩容的时候是扩大两倍, 有一点不好, 就是素数乘2之后会变成偶数, 模一个偶数会容易导致分布不均匀, 所以做一些改进, 那就是使用上面的素数表
上面两个条件判断的修改如下
// 上面那个素数表
private final int[] capacity = {53, 97, 193, 389, 769, 1543, 3079, 6151,
12289, 24593, 49157, 98317, 196613, 393241, 786433, 1572869, 3145739,
6291469, 12582917, 25165843, 50331653, 100663319, 201326611, 402653189,
805306457, 1610612741}; // 最大不能超过int的表示范围
private int capacityIndex = 0; // 初始容量是53
扩容:
if(size >= upperTol * M && capcityIndex+1 < capacity.length){ // 用除法会有误差
capcityIndex++;
resize(capacity[capcityIndex]);
}
缩容:
if(size < lowerTol * M && capacityIndex-1 >= 0) { // 要防止缩太小
capacityIndex--;
resize(capacity[capacityIndex]);
}
哈希函数和扩容缩容函数如下
// 哈希函数
private int hash(K key){
return (key.hashCode() & 0x7fffffff) % M; // 去掉符号, 再转为索引
}
private void resize(int newM) {
TreeMap<K, V>[] newHashTable = new TreeMap[newM];
// 初始化newM个索引, 每个索引是一个TreeMap
for(int i=0; i<newM; i++)
newHashTable[i] = new TreeMap<>();
int oldM = M; // 保存旧的M
this.M = newM; // 更新M, 因为hash()要用到M
for(int i=0; i<oldM; i++){ // 遍历旧的所有索引
TreeMap<K, V> map = hashtable[i];
for(K key: map.keySet()){ // 遍历索引上的TreeMap的每个键值
newHashTable[hash(key)].put(key, map.get(key));
}
}
this.hashtable = newHashTable;
}
适用范围
Java标准库中
有序集合, 有序映射用的是平衡树
无序集合, 无序映射用的是哈希表
实现
总的代码如下
HashTable.java
import java.util.TreeMap;
public class HashTable<K, V> {
private final int[] capacity
= {53, 97, 193, 389, 769, 1543, 3079, 6151, 12289, 24593,
49157, 98317, 196613, 393241, 786433, 1572869, 3145739, 6291469,
12582917, 25165843, 50331653, 100663319, 201326611, 402653189, 805306457, 1610612741}; // 最大不能超过int的表示范围
private static final int upperTol = 10;
private static final int lowerTol = 2;
private int capacityIndex = 0; // 初始容量是53
private TreeMap<K, V>[] hashtable;
private int M; // hashtable的长度
private int size; // 存储的元素个数
public HashTable(){
this.M = capacity[capacityIndex];
size = 0;
hashtable = new TreeMap[M];
for(int i=0; i<M; i++)
hashtable[i] = new TreeMap<>(); // 每个索引位置都连一个TreeMap
}
// 哈希函数
private int hash(K key){
return (key.hashCode() & 0x7fffffff) % M; // 去掉符号, 再转为索引
}
public int getSize(){
return size;
}
// 添加元素
public void add(K key, V value){
TreeMap<K, V> map = hashtable[hash(key)]; // 找到索引位置
// 如果已经存在, 就更新
if(map.containsKey(key)){ // 看那个索引位置连的树中有没有我们要的键
map.put(key, value);
}
else{
map.put(key, value);
size++;
if(size >= upperTol * M && capacityIndex+1 < capacity.length){ // 用除法会有误差
capacityIndex++;
resize(capacity[capacityIndex]);
}
}
}
// 删除元素
public V remove(K key){
TreeMap<K, V> map = hashtable[hash(key)]; // 找到索引位置
V ret = null;
if(map.containsKey(key)){
ret = map.remove(key);
size--;
if(size < lowerTol * M && capacityIndex-1 >= 0) { // 要防止缩太小
capacityIndex--;
resize(capacity[capacityIndex]);
}
}
return ret;
}
private void resize(int newM) {
TreeMap<K, V>[] newHashTable = new TreeMap[newM];
// 初始化newM个索引, 每个索引是一个TreeMap
for(int i=0; i<newM; i++)
newHashTable[i] = new TreeMap<>();
int oldM = M;
this.M = newM;
for(int i=0; i<oldM; i++){
TreeMap<K, V> map = hashtable[i];
for(K key: map.keySet()){
newHashTable[hash(key)].put(key, map.get(key));
}
}
this.hashtable = newHashTable;
}
// 修改
public void set(K key, V value){
TreeMap<K, V> map = hashtable[hash(key)];V ret = null;
if(!map.containsKey(key))
throw new IllegalArgumentException(key + "does not exist!");
map.put(key, value);
}
// key是否存在
public boolean contains(K key){
return hashtable[hash(key)].containsKey(key);
}
// 通过key获取value
public V get(K key){
return hashtable[hash(key)].get(key);
}
}