HDU6333 Problem B. Harvest of Apples【组合数+莫队+费马小快速幂】

题意：给m,n 求S(m,n) S(m,n) = C(m,n) + C(m,n-1)+...+C(m,0);

思路：

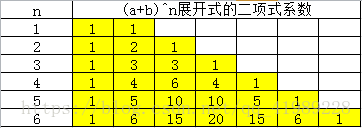
在讲思路之前 先写一个杨辉三角的规律

不难发现从第二行起 每行除1以外的每一个数都等于它肩上两个数的和

即 C(n,m) = C(n-1,m-1) + C(n-1,m)

通过上面的公式 我们还可以推出S(n,m) = 2*S(n-1,m) - C(n-1,m)

举个例子  S(5,3) = C(5,3) + C(5,2) + C(5,1) + C(5,0)

而 C(5,3) = C(4,2) + C(4,3)   

C(5,2) = C(4,1) + C(4,2)

C(5,1) = C(4,0) + C(4,1)   

C(5,0) = C(4,0) = 1

所以 S(5,3) = C(4,3) + C(4,2) + C(4,2) + C(4,1) + C(4,1) + C(4,0) + C(4,0) = 2*S(4,3) - C(4,3)

说下思路 莫队  l , r 分别指向 S(n,m) 中的 n 和 m 配合下列公式食用 其他就是套模版了

二项式系数：

(1) C(n,m) = n! / ((n-m)! * m!)

(2) C(n,m) = C(n-1,m-1) + C(n-1,m)

二项式系数和：

(3) S(n,m+1) = S(n,m) + C(n,m+1)

由(3)可得：(4) S(n,m-1) = S(n,m) - C(n,m)

(5) S(n+1,m) = 2*S(n,m) - C(n,m)

由(5)可得：(6) S(n-1,m) = (S(n,m) + C(n-1,m)) / 2

蓝后再丢一个费马小快速幂求逆元的模版：https://blog.csdn.net/nickwong_/article/details/38797629

代码：

#include 
#define ll long long
#define maxn 100005
#define mod 1000000007
using namespace std;

ll fac[maxn];//阶乘
ll inv[maxn];//逆元
ll inv2;//2的逆元 
ll ans[maxn];
ll b;
int pos[maxn]; 

struct Mo{
	int l,r,id;
}a[maxn];

bool cmp(Mo x, Mo y) {
	return pos[x.l] == pos[y.l] ? x.r < y.r : x.l < y.l;
}

//费马小+快速幂求逆元模版 
ll Pow(ll x, ll y) {
	ll anss = 1;
	while(y) {
		if(y&1) anss = anss*x%mod;
		x = x * x % mod;
		y >>= 1; 
	}
	return anss;
} 

void init() {
	//阶乘
	fac[0] = fac[1] = 1;
	for(int i = 2; i < maxn; i++) {
		fac[i] = i * fac[i - 1] % mod;
	} 
	
	//求阶乘的逆元
	//因为mod是质数 且mod与fac数组里每个数最大公约数是1 
	//所以根据费马小定理
	inv[maxn - 1] = Pow(fac[maxn - 1], mod - 2);
	for(int i = maxn - 2; i >= 0; i--) {
		inv[i] = inv[i + 1] * (i + 1) % mod;
	}
	
	//因为公式里面有/2 所以求2的逆元
	inv2 = Pow(2,mod - 2); 
}

//求C(n,m) 
ll Comb(int n, int m) {
	return fac[n] * inv[m] % mod * inv[n-m] % mod; 
}

//S(n,m+1) 公式(3) 
void addR(int n, int m) {
	b = (b + Comb(n,m)) % mod;
}

//S(n+1,m) 公式(5)
void addL(int n, int m) {
	b = (2 * b % mod - Comb(n-1,m) + mod) % mod;
}

//S(n,m-1) 公式(4)
void delR(int n, int m) {
	b = (b - Comb(n,m) + mod) % mod;
}

//S(n-1,m) 公式(6) 
void delL(int n, int m) {
	b = (b + Comb(n - 1,m)) % mod * inv2 % mod;
}

int main() {
	int t;
	scanf("%d",&t);
	int len = sqrt(t);
	init();
	for(int i = 1; i <= t; i++) {
		scanf("%d %d",&a[i].l, &a[i].r);
		pos[i] = i/len;
		a[i].id = i;
	}
	sort(a+1,a+1+t,cmp);
	int l = 1, r = 1;
	b = 2;
	for(int i = 1; i <= t; i++) {
		while(l < a[i].l) addL(++l,r);
		while(r < a[i].r) addR(l,++r);
		while(l > a[i].l) delL(l--,r);
		while(r > a[i].r) delR(l,r--);
		ans[a[i].id] = b;
	}
	for(int i = 1; i <= t; i++) {
		printf("%lld\n",ans[i]);
	} 
}