【图形学】基于点云生成树木模型

很久之前就想尝试有关于点云方面的知识，但是一直耽搁到现在，一方面感觉很难不知道如何下手。最近看了师兄发来的论文后，我发现基于点云生成树木模型也并没有想象中那么难。

参考论文：Knowledge and Heuristic Based Modeling of Laser-Scanned Trees. Hui Xu，Nathan Gossett， Baoquan Chen.

参考博客：https://blog.csdn.net/Mahabharata_/article/details/79511894

因为现在三维扫描设备发展非常迅速，利用这些设备我们可以很轻易的获取到各种物体的点云数据，而从点云重新恢复出物体的三维模型可以让三维模型更符合现实以至于让人难以区分的程度，所以这是非常有意义的一项工作。本文主要讲的是从点云恢复出树木模型。

先放出我的程序结果及技术路线：

 

(a) 分离树叶点云和枝干点云	(b) 获取枝干点云
(c) 每个点到根的最短路径	(d) 生成聚类并生成 bin
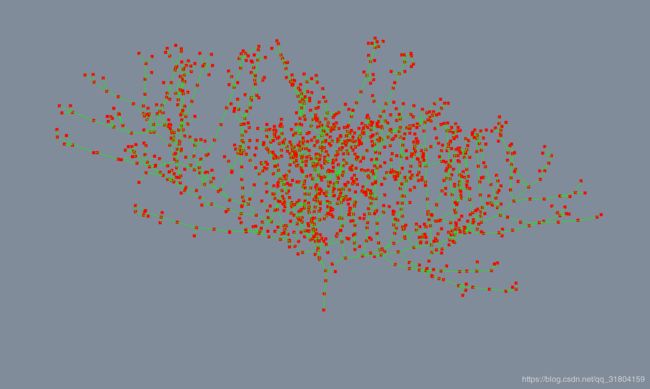
(e) 根据 bin 获得树骨架	(f) 根据骨架绘制树
(g) 骨架优化	(h) 最终效果

效果是不是还可以呢，其实复现出这种效果并不难。别着急，往下看。

一、知识点储备

担心自己能否实现这样的代码？只要会用c++和opengl就够了！

程序里主要用到的数据结构和算法是：kd-Tree、迪杰斯特拉算法。

kd-Tree的话我是自己实现了一遍，当然你也可以直接使用别人封装好的kdTree，我是建议自己实现一下，也不是很难，半天应该就能写出来了，至于迪杰斯特拉算法，这个从一开始就学过N次的求最短路径的算法就不多说了。

如果准备好了，那我们就开始了~

二、具体实现流程

 

1. 输入点云数据

若有Kinect可自行采取点云数据，如若没有也可以在网上下载一个树木模型用作测试。

2. 分离枝干点云和树叶点云

我们可以把模型中的竖直方向最低点当做根节点。我们设定一个半径r，如果从根节点开始，不断的把临近的点（到根节点距离小于r的点）加入到枝干点云集合中，最终剩下的点便是树叶点云。这样做是因为，对于树木来说其枝干点云的密度显然是比树叶点云的密度大的，所以选取一个合适的r便可以将二者区分出来。

我们采用kd-Tree进行搜索，可以看出，我们从下面看出，在10万的数据量上，我们寻找到所有的枝干点仅仅花费了0.17s！！！

感兴趣的同学可以试一下用循环来搜索数据，和用kd-tree进行搜索对比，可以更直观的感受到kd-tree的强大

下面放出分离点云的伪代码：

 

    bool mask[m_vertex.size()];//标记点云中某点是否找过，m_vertex存放全部点云数据
    memset(mask,0,m_vertex.size()*sizeof(bool));
    mask[m_rootIndex] = true;//标记根节点已找过
    //m_branchPts用于保存枝干点云
    m_branchPts.push_back(m_vertex[m_rootIndex]);  //把最低点当成枝干点云的第一个点

    
    kdTree.init(box,m_vertex);//对KdTree进行初始化，box为模型的包围盒
  
    //寻找枝干点
   
    for(int i =0; i< m_branchPts.size();i++)
    {
        Vector neighbors = kdTree.search(radius,m_branchPts[i]);
        //        int step = m_branchPts.size();
        for( int j =0; j< neighbors.size();j++)
        {
            if(mask[neighbors[j]]==false)  //如果没找过该点，则加入到枝干点云中
            {
                mask[neighbors[j]]=true;
                m_branchPts.push_back(m_vertex[neighbors[j]]);
            }
        }
    }

完成这一步之后我们就可以的到下面这张图的效果了，可以绘制一下，满满的幸福感。右图即为我们得到的枝干点云

    

3. 得到每一个点到根节点的最短路径

要使用迪杰斯特拉算法的到最短路径，我们需要先得到连通图。连通图其实就是顶点和边，知道顶点和边很容易就构建出连通图，然后根据连通图我们就能得到每一个结点到根节点的最短路径。至于为什么做这一步，请往下看（3和4步均是为第5步服务的）。伪代码如下：

    KdTree kdBranch;   //构建枝干点云的kd-tree
    kdBranch.init(box,m_branchPts);
 

    for( int i =0; i< m_branchPts.size(); i++)
    {
        maskBranch[i] = true;

     Vector neighbors = kdTree.search(radius,m_branchPts[i]);
  
        for( int j =0; j< neighbors.size();j++)
        {
            if(mask[neighbors[j]]==false)  
            {
                 m_lines.push_back(Line(i,neighbors[j]));//保存所有相邻的线
            }
        }

    }


    Graph G(m_branchPts,m_lines);  //生成连通图

    //dijkstra方法寻找最短路径
    Dijkstra findPath;
    findPath.ShortestPath(G,0);//0表示到根节点
 
   Vector m_paths = findPath.getShortestPath(G,0);  //把每一个结点到根节点的最短路径保存到m_paths中

写到这，基本上一大部分的工作已经完成了，如果现在绘制出来就会的到下面这个效果

下面是程序耗时，大家可以参照一下。枝干点的总数目为：49166

4. 生成聚类并生成 bin

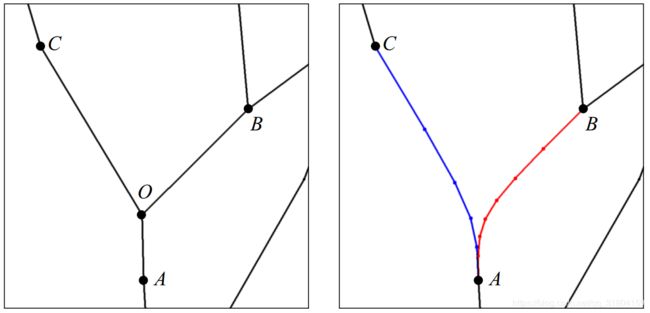
首先明确一下bins和bin的概念，下图是截取自论文中的一幅图，在下面左图中我们可以把框起来的绿色点集或者青色点集称为一个聚类或者是bins，在下面右图中我们可以把圈框出的绿色或是红色点集称为一个bin。

原文中对下图的描述是：The lengths of the shortest paths are quantized and the points are clustered into bins. 即量化最短路径的长度聚类生成bins。就是说我们根据每个点到根节点的最短距离划分成不同区域，把到根节点距离相似的点放在一个bins中，然后我们再把一个bins分成若干个小bin

                                                   

我的实现细节：首先我们可以很简单的获取到距离根节点最远的距离记为maxdist,然后我们定义一个数字numOfBinsLevel，就是说把这个树分为多少个bins。至于如何把bins分为若干个bin，那么只要对每一个bins进行搜索，默认从第一个点开始搜索一直把bins中临近的点加入到一个bin中，如此迭代一直到bins中的点被搜索完为止。如上面右图中的红色点集就是分出的一个bin，其所在的bins最终会分成两个bin。

伪代码如下：

Vector > getBins(float maxdist, int numOfBinsLevel, Vector &branchPts, Vector &paths)
{
    Vector > bins;  //存储点
    float len = maxdist/numOfBinsLevel;
    bins.resize(numOfBinsLevel);
    for( int i = 0; i< paths.size(); i++)
    {
        bool find = false;
        for( int j =0;j =len*j) //找到范围区间的点
            {
                m_colors.push_back(color[j%color.size()]);
                bins[j].push_back( branchPts[paths[i].path.first()] );
                find = true;
                break;

            }
        }
 
    }
    return bins;
}

当所有准备就绪后，我们可以将这些点按照bin绘制出来，每一个bin分配同一种颜色，便可得到下面这种效果

5.  获得树的骨架

先说明树骨架采用的数据结构：

struct Branch
{
public:
    QList nodes;  //一个枝干的点
    QList offspring; //连接的子枝干
    Branch* father;   //父枝干
    float branchWidth; //枝干宽度
    QList > leafs;  //保存叶子的位置和密度
    QList > linkNode; //连接叶子的枝干点和他的朝向

} ;

如果能获得树的骨架那么这个树木建模方法也就算基本完成了。我们把每一个bin的中心点（点的坐标和取平均）当做树骨架的一个节点（看到这里就明白为什么进行第3和第4步了吧），但是连接所有的节点组成树的骨架也是一个小难点，这里可以采用方法：连通图的深度优先搜索+KdTree的最邻近查询的策略。也可以自己设计连接算法，我这里使用的是我自己想的一个连接方法。

我这里的做法是在分离bins的同时连接树骨架，有些复杂，但是实现起来并不难，但是为了纪念我苦苦思索的成果，我还是写一下流程。

算法流程是：1. 从bins分离bin的过程中定义一个 levelbins，其存储了每一个距离范围水平的所有bin

                      2 .若levelbins中仅有一个bin，那么就算出该bin的中心点center，然后把该点连到到距离现有骨架中点最近的点                                 m。 即连在m所在的枝干

                     3. 若levelbins中有多个bin，那么我们需要对每一个bin进行分析，分别把bin对应的中心点连到到距离现有骨架中点                           最近的点。

实现效果如下（emm这个例子的话看起来确实有些乱，最好放大看图片）：

6. 绘制及优化骨架

这个就需要知道树木模型在计算机是如何表示的，请点击这里。

绘制出的初步结果如下，结果么，看起来是还不错，但是总感觉有些过于僵硬：

造成过于僵硬的原因是由于在大多数情况下尖锐的过渡就不像树的真实外观，因此应该对它们进行平滑处理。

下图角AOB和角AOC便过大，我们对骨架进行Hermite曲线优化：

 

Hermite曲线是一个很简单的差值，这里不做赘述。

曲线优化结果为下图，是不是看起来更自然更平滑了呢

7.  树叶

我们如何把树叶加上呢，是不是发现我们忽略了一些我们的数据，那就是树叶点云。这里我们可以采取简单一些的方法，

（1）我们获得同一种树的不同数目的树叶，如下图：

（2）我们对每一个骨架中的点在树叶点云中进行范围搜索（搜索半径可自行标定，记为R），然后搜索的出来的树叶点的数目便记为在该骨架点中树叶的密度，密度越大则可放置越多数目的树叶。

（3）树叶的朝向计算：

对于每个树叶位置L，我们四边形（树叶在计算机中的表示）连接到其最近的可行骨架节点S，我们把S的上一个骨架点到S的方向记为向量d。我们的到树叶的法向量为： 这里要好好想想哦。

8. 最终效果

三、总结

写到这就已经结束了，其实整篇下来并没有特别难的步骤，这里面稍微要费点脑子的可能就是如何组织自己的数据结构了。

我当时写这个程序大概写了一周左右，完整的实现出这样的一个程序对我来说也是一种很大的提升，而且做完这个我也非常有成就感，这就是写程序的乐趣所在吧hhh，希望本博客对大家有所帮助。

文笔不好，写的不好的地方请多担待。