三、【python计算机视觉编程】图像到图像的映射
图像到图像的映射
- (一)单应性变换
- (1)直接线性变换算法(DLT)
- (2)仿射变换(affine)
- (二)图像扭曲
- (1)图像中的图像
- (2)分段仿射扭曲
- (3)图像配准
- (三)创建全景图
- (1)RANSAC
- (2)稳健的单应性矩阵估计
- (3)拼接图像
- 更新:重新进行该实验
- 第一次实验代码与实验结果
- 第二次实验,下面进行两张图片的拼接实验
(一)单应性变换
概念:
单应性变换是将一个平面内的点映射到另一个平面内的二维投影变换。在这里,平面是指图像或者三维中的平面表面。单应性变换具有很强的实用性,如图像配准、图像纠正和纹理扭曲,以及创建全景图像。本质上,单应性变换H,按照下面的方程映射二维的点(齐次坐标意义下):

对于图像平面内的点,齐次坐标是个非常有用的表示方法。点的齐次坐标是依赖于其尺度定义的,所以,单应性矩阵具有8个独立的自由度。
简单的理解为:用来描述物体在世界坐标系和像素坐标系之间的位置映射关系。对应的变换矩阵称为单应性矩阵。
(ps:什么是世界坐标系? 它是系统的绝对坐标系,在没有建立用户坐标系之前画面上所有点的坐标都是以该坐标系的原点来确定各自的位置的。其定义为:1、 带有小圆的圆心为原点ow,xw轴水平向右,yw轴向下,zw由右手法则确定.,v′n为实时图中对应的统计特征向量。2、 设一个基准坐标系Xw—Yw—Zw称为世界坐标系,(xw,yw,zw)为空间点P在世界坐标系下的坐标.(u,v)为P点在图像直角坐标系下的坐标)
基本变换及其数学表达式:
-
刚体变换(rigid transformation):旋转和平移变换/rotation,translation, 3个自由度,点与点之间的距离不变。
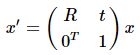
其中, R为2*2旋转矩阵,t为2维列向量,0T为0的二维行向量 -
相似变换(similarity transformation):增加了缩放尺度,四个自由度,点与点之间的距离比不变。
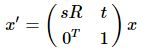
其中,s为缩放尺度 -
仿射变换(affine transformation)::仿射变换和相似变换近似,不同之处在于相似变换具有单一旋转因子和单一缩放因子,仿射变换具有两个旋转因子和两个缩放因子,因此具有6个自由度。 不具有保角性和保持距离比的性质,但是原图平行线变换后仍然是平行线。

其中,A为2*2的非奇异矩阵,可被分解为如下:A=R(θ)R(−ϕ)DR(ϕ)。
R(θ)R(ϕ)R(θ)R(ϕ) 为旋转矩阵,D为对角阵

λ1和λ2λ1和λ2可以看做两个方向的缩放比 -
投影变换(projective transformation):也叫作单应性变换。投影变换是齐次坐标下非奇异的线性变换。然而在非齐次坐标系下却是非线性的,这说明齐次坐标的发明是很有价值的。投影变换比仿射变换多2个自由度,具有8个自由度。上面提到的仿射变换具有的“不变”性质,在投影变换中已不复存在了。尽管如此,它还是有一项不变性,那就是在原图中保持共线的3个点,变换后仍旧共线。投影变换表示如下:

其中,V=(v1,v2)T -
透视变换:透视变换将图像投影到一个新的视平面,是二维到三维再到另一个二维(x’, y’)空间的映射。透视变换前两行和仿射变换相同,第三行用于实现透视变换。透视变换前后,原来共线的三个点,变换之后仍然共线。

以上公式设变换之前的点是z值为1的点,它三维平面上的值是x,y,1,在二维平面上的投影是x,y,通过矩阵变换成三维中的点X,Y,Z,再通过除以三维中Z轴的值,转换成二维中的点x’,y’.
从以上公式可知,仿射变换是透视变换的一种特殊情况.它把二维转到三维,变换后,再转映射回之前的二维空间(而不是另一个二维空间)。
估计单应性矩阵:
首先,我们假设两张图像中的对应点对齐次坐标为(x’,y’,1)和(x,y,1),单应矩阵H定义为:

则有:
[ x ′ y ′ 1 ] ∼ [ h 11 h 12 h 13 h 21 h 22 h 23 h 31 h 32 h 33 ] [ x y 1 ] \begin{bmatrix} x'\\ y' \\ 1 \end{bmatrix} \sim \begin{bmatrix} h_{11} & h_{12}& h_{13}\\ h_{21}& h_{22} &h_{23} \\ h_{31} & h_{32} & h_{33} \end{bmatrix}\begin{bmatrix} x\\ y\\ 1 \end{bmatrix} ⎣⎡x′y′1⎦⎤∼⎣⎡h11h21h31h12h22h32h13h23h33⎦⎤⎣⎡xy1⎦⎤
矩阵展开后有3个等式,将第3个等式代入前两个等式中可得:
x ′ = h 11 x + h 12 y + h 13 h 31 x + h 32 y + h 33 {x}'=\frac{h_{11}x+h_{12}y+h_{13}}{h_{31}x+h_{32}y+h_{33}} x′=h31x+h32y+h33h11x+h12y+h13
y ′ = h 21 x + h 22 y + h 23 h 31 x + h 32 y + h 33 {y}'=\frac{h_{21}x+h_{22}y+h_{23}}{h_{31}x+h_{32}y+h_{33}} y′=h31x+h32y+h33h21x+h22y+h23
也就是说,一个点对对应两个等式。
下面还说明一下为什么单应性矩阵是8个自由度,而不是9个呢?
由于计算使用的是齐次坐标系,通俗来说就是可以进行任意尺度的缩放。假设我们把hij乘以任意一个非零常数k并不改变等式结果,所以单应矩阵H只有8个自由度。
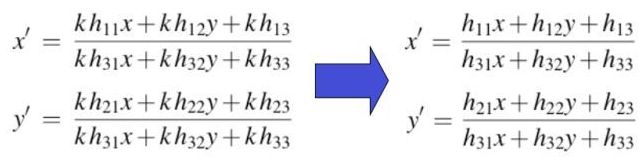
继续介绍两种方法在8个自由度下矩阵H的计算过程:
方法一,直接设置 h33=1,那么上述等式变为:
x ′ = h 11 x + h 12 y + h 13 h 31 x + h 32 y + 1 {x}'=\frac{h_{11}x+h_{12}y+h_{13}}{h_{31}x+h_{32}y+1} x′=h31x+h32y+1h11x+h12y+h13
y ′ = h 21 x + h 22 y + h 23 h 31 x + h 32 y + 1 {y}'=\frac{h_{21}x+h_{22}y+h_{23}}{h_{31}x+h_{32}y+1} y′=h31x+h32y+1h21x+h22y+h23
方法二,将H添加约束条件,将H矩阵模变为1:
x ′ = h 11 x + h 12 y + h 13 h 31 x + h 32 y + h 33 {x}'=\frac{h_{11}x+h_{12}y+h_{13}}{h_{31}x+h_{32}y+h_{33}} x′=h31x+h32y+h33h11x+h12y+h13
y ′ = h 21 x + h 22 y + h 23 h 31 x + h 32 y + h 33 {y}'=\frac{h_{21}x+h_{22}y+h_{23}}{h_{31}x+h_{32}y+h_{33}} y′=h31x+h32y+h33h21x+h22y+h23
h 11 2 + h 12 2 + h 13 2 + h 21 2 + h 22 2 + h 23 2 + h 31 2 + h 32 2 + h 33 2 = 1 h_{11}^{2}+h_{12}^{2}+h_{13}^{2}+h_{21}^{2}+h_{22}^{2}+h_{23}^{2}+h_{31}^{2}+h_{32}^{2}+h_{33}^{2}=1 h112+h122+h132+h212+h222+h232+h312+h322+h332=1
以第二种方法(用第一种也类似)为例继续推导,我们将如下等式(包含||H||=1约束):
x ′ = h 11 x + h 12 y + h 13 h 31 x + h 32 y + h 33 {x}'=\frac{h_{11}x+h_{12}y+h_{13}}{h_{31}x+h_{32}y+h_{33}} x′=h31x+h32y+h33h11x+h12y+h13
y ′ = h 21 x + h 22 y + h 23 h 31 x + h 32 y + h 33 {y}'=\frac{h_{21}x+h_{22}y+h_{23}}{h_{31}x+h_{32}y+h_{33}} y′=h31x+h32y+h33h21x+h22y+h23
乘以分母展开,得到:
( h 31 x + h 32 y + h 33 ) x ′ = h 11 x + h 12 y + h 13 (h_{31}x+h_{32}y+h_{33}){x}'=h_{11}x+h_{12}y+h_{13} (h31x+h32y+h33)x′=h11x+h12y+h13
( h 31 x + h 32 y + h 33 ) y ′ = h 21 x + h 22 y + h 23 (h_{31}x+h_{32}y+h_{33}){y}'=h_{21}x+h_{22}y+h_{23} (h31x+h32y+h33)y′=h21x+h22y+h23
整理,得到:
h 11 x + h 12 y + h 13 − h 31 x x ′ − h 32 y x ′ − h 33 x ′ = 0 h_{11}x+h_{12}y+h_{13}-h_{31}x{x}'-h_{32}y{x}'-h_{33}{x}'=0 h11x+h12y+h13−h31xx′−h32yx′−h33x′=0
h 21 x + h 22 y + h 23 − h 31 x y ′ − h 32 y y ′ − h 33 y ′ = 0 h_{21}x+h_{22}y+h_{23}-h_{31}x{y}'-h_{32}y{y}'-h_{33}{y}'=0 h21x+h22y+h23−h31xy′−h32yy′−h33y′=0
对于上述方程可写成一个矩阵与一个向量相乘,即:
[ x y 1 0 0 0 − x x ′ − y x ′ − x ′ 0 0 0 x y 1 − x y ′ − y y ′ − y ′ ] h = 0 \begin{bmatrix}x & y & 1 & 0 & 0 & 0 & -xx' & -yx' & -x' \\ 0 & 0 & 0 & x & y & 1 & -xy' & -yy' & -y'\end{bmatrix}h=0 [x0y0100x0y01−xx′−xy′−yx′−yy′−x′−y′]h=0
其中, h = [ h 11 , h 12 , h 13 , h 21 , h 22 , h 23 , h 31 , h 32 , h 33 ] T h=[h_{11},h_{12},h_{13},h_{21},h_{22},h_{23},h_{31},h_{32},h_{33}]^{T} h=[h11,h12,h13,h21,h22,h23,h31,h32,h33]T,是一个9维的列向量。令
A = [ x y 1 0 0 0 − x x ′ − y x ′ − x ′ 0 0 0 x y 1 − x y ′ − y y ′ − y ′ ] A=\begin{bmatrix}x & y & 1 & 0 & 0 & 0 & -xx' & -yx' & -x' \\ 0 & 0 & 0 & x & y & 1 & -xy' & -yy' & -y'\end{bmatrix} A=[x0y0100x0y01−xx′−xy′−yx′−yy′−x′−y′]
可以记为 : A h = 0 Ah=0 Ah=0 这只是1对点所得到的矩阵A。
由于我们是采用齐次坐标(即(x,y,1))来表示平面上的点,所以存在一个非零的标量s,使得 b 1 = s H a T b_{1}=sHa^{T} b1=sHaT和 b = s H a T b=sHa^{T} b=sHaT都表示同一个点b。若令 s = 1 h 33 s=\frac{1}{h33} s=h331,则 1 h 33 H \frac{1}{h_{33}}H h331H为:
1 h 33 H = [ h 11 h 33 h 12 h 33 h 13 h 33 h 21 h 33 h 22 h 33 h 23 h 33 h 31 h 33 h 32 h 33 1 ] \frac{1}{h_{33}}H=\begin{bmatrix} \frac{h_{11}}{h_{33}} & \frac{h_{12}}{h_{33}} & \frac{h_{13}}{h_{33}}\\ \frac{h_{21}}{h_{33}} & \frac{h_{22}}{h_{33}} & \frac{h_{23}}{h_{33}}\\ \frac{h_{31}}{h_{33}} & \frac{h_{32}}{h_{33}} & 1 \end{bmatrix} h331H=⎣⎢⎡h33h11h33h21h33h31h33h12h33h22h33h32h33h13h33h231⎦⎥⎤
由此看出,矩阵H只有8个变量(8个自由度)。所以只需要4个点对,然后通过解线性方程组就可以求得矩阵H。(也可以多于4个点对)
下面介绍几种实现对点进行归一化和转换齐次坐标的功能函数:
在进行点和变换处理时,会按照列优先的原则存储这些点。
#normalize() 函数可以实现对点进行归一化和转换齐次坐标的功能
def normalize(points):
"""在其次坐标意义下,对点集进行归一化,使最后一行为1"""
for row in points:
row /= points[-1]
return points
def make_homog(points):
"""将点集(dim*n的数组)转换为齐次坐标表示"""
return vstack((points,ones((1,points.shape[1]))))
(1)直接线性变换算法(DLT)
单应性矩阵是由两幅图像或者平面中对应点计算出来的,一个完全射影变换具有8个自由度,根据对应点约束,每个对应点可以写出两个方程,分别对应于x和y坐标。因此计算单应性矩阵H需要4个对应点对。
概念:
DLT是给定4个或者更多对应点对矩阵,来计算单应性矩阵H的算法。将单应性矩阵H作用在对应点对上,重新写出该方程,可以得到下面的式子:

或者
![]()
其中A是一个具有对应点对二倍数量行数的矩阵。
特点:
- 不归心,不定向
- 不需要内外方位元素的起始值
- 物方空间需布置一组控制点
- 特别适合于处理非量测相机所摄影像
- 本质上是一种空间后交-前交解法
求解方法:
在图像拼接中,得到了两张图像的特征匹配,两个点集分别记作 X X X和 X ′ X′ X′。用单应性变换来拟合二者的关系,可表达为:
c ( u v 1 ) = H ( x y 1 ) c\begin{pmatrix}u \\ v \\1 \end{pmatrix}=H\begin{pmatrix}x \\ y \\1 \end{pmatrix} c⎝⎛uv1⎠⎞=H⎝⎛xy1⎠⎞
其中, ( u v 1 ) T \begin{pmatrix}u & v & 1\end{pmatrix}^{T} (uv1)T是 X ′ X′ X′中特征点的坐标, ( x y 1 ) T \begin{pmatrix}x & y & 1\end{pmatrix}^{T} (xy1)T是 X X X中特征点的坐标, H H H是单应性矩阵,代表它们之间的变换关系。 H H H是个3×3的矩阵,有8个自由度,所以待求未知参数有8个。
H = [ h 1 h 2 h 3 h 4 h 5 h 6 h 7 h 8 h 9 ] H = \begin{bmatrix} h_{1} & h_{2}& h_{3}\\ h_{4}& h_{5} &h_{6} \\ h_{7} & h_{8} & h_{9} \end{bmatrix} H=⎣⎡h1h4h7h2h5h8h3h6h9⎦⎤
DLT算法推导过程: 将上式展开,前2行分别被第3行相除,得到 :
− h 1 x − h 2 y − h 3 + ( h 7 x + h 8 y + h 9 ) u = 0 −h_{1}x−h_{2}y−h_{3}+(h_{7}x+h_{8}y+h_{9})u=0 −h1x−h2y−h3+(h7x+h8y+h9)u=0
− h 4 x − h 5 y − h 6 + ( h 7 x + h 8 y + h 9 ) v = 0 −h_{4}x−h_{5}y−h_{6}+(h_{7}x+h_{8}y+h_{9})v=0 −h4x−h5y−h6+(h7x+h8y+h9)v=0
上面的两条式子可以整理为:
A i h = 0 A_{i}h=0 Aih=0
其中,
A = [ − x − y − 1 0 0 0 u x u y u 0 0 0 − x − y − 1 v x v y v ] A=\begin{bmatrix}-x & -y & -1 & 0 & 0 & 0 & ux & uy & u \\ 0 & 0 & 0 & -x & -y & -1 & vx & vy & v\end{bmatrix} A=[−x0−y0−100−x0−y0−1uxvxuyvyuv]
h = [ h 1 , h 2 , h 3 , h 4 , h 5 , h 6 , h 7 , h 8 , h 9 ] h=[h_{1},h_{2},h_{3},h_{4},h_{5},h_{6},h_{7},h_{8},h_{9}] h=[h1,h2,h3,h4,h5,h6,h7,h8,h9]
由未知变量的个数可知,求解出 H H H至少需要4对匹配点。通常情况下为了得到更稳定的结果,会用到多于4对的特征匹配。所以,这个方程会变成超定的,可以将最小二乘解作为最后的解。
将这些对应点对方程的系数堆叠到一个矩阵中,我们可以使用SVD(Singular Value Decomposion,奇异值分解)算法找到H的最小二乘解。下面是该算法的代码:
def H_from_points(fp,tp):
"""使用直接线性变换DLT方法,计算单应性矩阵H,使fp映射到tp。点自动进行归一化"""
#检查点对的两个数组中点的数目是否相同,如果不相同,会抛出异常信息
if fp.shape != tp.shape:
raise RuntimeError('number of points do not match')
#对点进行归一化(对数值计算很重要)
#----映射起始点---
m = mean(fp[:2],axis=1)
maxstd = max(std(fp[:2],axis=1)) + 1e-9
C1 = diag([1/maxstd,1/maxstd,1])
C1[0][2] = -m[0]/maxstd
C1[1][2] = -m[1]/maxstd
fp = dot(C1,fp)
#---映射对应点---
m = mean(tp[:2],axis=1)
maxstd = max(std(tp[:2],axis=1)) + 1e-9
C2 = diag([1/maxstd,1/maxstd,1])
C2[0][2] = -m[0]/maxstd
C2[1][2] = -m[1]/maxstd
tp = dot(C2,tp)
#创建用于线性方法的矩阵,对于每个对应对,在矩阵中会出现两行数值
nbr_correspondences = fp.shape[1]
A = zeros((2*nbr_correspondences,9))
for i in range(nbr_correspondences):
A[2*i] = [-fp[0][i],-fp[1][i],-1,0,0,0,
tp[0][i]*fp[0][i],tp[0][i]*fp[1][i],tp[0][i]]
A[2*i+1] = [0,0,0,-fp[0][i],-fp[1][i],-1,
tp[1][i]*fp[0][i],tp[1][i]*fp[1][i],tp[1][i]]
U,S,V = linalg.svd(A)
H = V[8].reshape((3,3))
#反归一化
H = dot(linalg.inv(C2),dot(H,C1))
#归一化,然后返回
return H/H[2,2]
对这些点进行归一化操作,其均值为0,方差为1,因为算法的稳定性取决于坐标的表示情况和部分数值计算的问题,所以归一化操作非常重要。
操作方法:
使用对应点来构造矩阵A,最小二乘解即为矩阵SVD分解后所得矩阵V的最后一行。该行经过变形后得到矩阵H。然后对这个矩阵进行处理和归一化,返回输出。
(2)仿射变换(affine)
概念:
一种二维坐标到二维坐标之间的线性变换(相同平面),它保持了二维图形的“平直性”(直线经过变换之后依然是直线)和“平行性”(二维图形之间的相对位置关系保持不变,平行线依然是平行线,且直线上点的位置顺序不变),但是角度会改变。任意的仿射变换都能表示为乘以一个矩阵(线性变换),再加上一个向量 (平移) 的形式。单应性变换有8个自由度,仿射有6个自由度, 因此需要三个对应点对来估计矩阵H,通过将最后两个元素设置为0,即h7=h8=0,仿射变换可以用上面的DLT算法估计得到。
简单来说, 就是允许图形任意倾斜,而且允许图形在两个方向上任意伸缩的变换。如图所示。仿射变换可以保持原来的线共点、点共线的关系不变,保持原来相互平行的线仍然平行,保持原来的中点仍然是中点,保持原来在一直线上的几段线段之间的比例关系不变。但是不能保持原来的线段长度不变,也不能保持原来的夹角角度不变。

仿射变换可以通过一系列的原子变换的复合来实现,包括:平移(Translation)、缩放(Scale)、翻转(Flip)、旋转(Rotation)和剪切(Shear)。

数学公式:

或者

保持了w=1,不具有投影变换所具有的强大变形能力。仿射变换包含一个可逆矩阵A和一个平移向量t=[tx,ty],仿射变换可以应用于图像扭曲等场景。
相似变换数学公式:(在上面有基本变换的叙述和公式)

或者

是一个包含尺度变化的二维刚体变换。上式中的向量s指定了变换的尺度,R是角度为θ的旋转矩阵,t=[tx,ty]在这里也是一个平移向量。如果s=1那么该变换能够保持距离不变。此时,该变换为刚体变换。
下面的函数使用对应点对来计算仿射变换矩阵:
def Haffine_from_points(fp,tp):
"""计算H,仿射变换,使得tp是fp经过仿射变换H得到的"""
if fp.shape != tp.shape:
raise RuntimeError('number of points do not match')
#对点进行归一化
#---映射的起始点---
m = mean(fp[:2],axis=1)
maxstd = max(std(fp[:2],axis=1)) + 1e-9
C1 = diag([1/maxstd,1/maxstd,1])
C1[0][2] = -m[0]/maxstd
C1[1][2] = -m[1]/maxstd
fp_cond = dot(C1,fp)
#---映射对应点---
m = mean(tp[:2],axis=1)
C2 = C1.copy() #两个点集,必须都进行相同的缩放
C2[0][2] = -m[0]/maxstd
C2[1][2] = -m[1]/maxstd
tp_cond = dot(C2,tp)
#因为归一化后点的均值为0,所以平移量为0
A = concatenate((fp_cond[:2],tp_cond[:2]),axis=0)
U,S,V = linalg.svd(A.T)
#如Hartley和Zisserman著的Multiple View Geometry in computer,scond eidtion所示,
#创建矩阵B和C
tmp = V[:2].T
B = tmp[:2]
C = tmp[2:4]
tmp2 = concatenate((dot(C,linalg.pinv(B)),zeros((2,1))),axis=1)
H = vstack((tmp2,[0,0,1]))
#反归一化
H = dot(linalg.inv(C2),dot(H,C1))
#归一化,然后返回
return H/H[2,2]
(二)图像扭曲
扭曲操作可以使用SciPy工具包中的ndimage包来完成。
from scipy.spatial import Delaunay
from numpy import *
from scipy import *
from PIL import *
import homography
from scipy import ndimage
import matplotlib
import matplotlib.pyplot as plt
from pylab import *
im = array(Image.open('mao/3.jpg').convert('L'))
H = array([[1.4,0.05,-100],[0.05,1.5,-100],[0,0,1]])
im2 = ndimage.affine_transform(im,H[:2,:2],(H[0,2],H[1,2]))
figure()
gray()
subplot(121)
imshow(im)
subplot(122)
imshow(im2)
show()

分析:
ndimage.affine_transform() 命令输出结果图像中丢失的像素用0来填充(即黑色部分),使用线性H[:2,:2]对图像进行变换,(H[0,2],H[1,2])是平移的向量。使用默认输出图像设置为
(1)图像中的图像
仿射扭曲的简单例子是,将图像或者图像中的一部分放置在另一幅图像中,使得它们能够和指定的区域或者标记物对齐。函数image_in_image() ,该函数的输入参数为两幅图像和一个坐标,用于实现上面叙述的例子。
编写实验代码:
# -*- coding: utf-8 -*-
"""
Created on Sat May 25 08:32:52 2019
@author: Administrator
"""
from scipy.spatial import Delaunay
from numpy import *
from scipy import *
from PIL import *
import homography
import homography
import warp
from scipy import ndimage
#仿射扭曲im1到im2的例子
im1 = array(Image.open('jimei/jimei9.jpg').convert('L'))
subplot(131)
title('jimei1')
axis('off')
imshow(im1)
im2 = array(Image.open('jimei/jimei5.jpg').convert('L'))
subplot(132)
title('jimei2')
axis('off')
imshow(im2)
#选定一些目标点,tp是映射目标位置
tp = array([[0,205,205,0],[500,500,100,100],[1,1,1,1]])
im3 = warp.image_in_image(im1,im2,tp)
#figure()
#gray()
subplot(133)
axis('equal')
axis('off')
imshow(im3)
show()
实验效果如下:
分析:
使用仿射变换将im1图像放置在im2图像上,其中(131)是集美大学校徽 ,(132)是集美大学最高那栋大楼,(133)是仿射图像,将集美大学的校徽icon放在图片的左上角位置。tp = array([[0,205,205,0],[500,500,100,100],[1,1,1,1]])可以调整图一映射到图二的位置。
(2)分段仿射扭曲
概念:
分段仿射扭曲是对应点集合之间最常用的扭曲方式,给定任意图像的标记点,通过将这些点进行三角剖分,然后使用仿射扭曲来扭曲每个三角形,可以将图像和另一幅图像的对应标记点扭曲对应。为了三角化这些点,可以使用狄洛克三角剖分方法。
编写代码:
# -*- coding: utf-8 -*-
from scipy.spatial import Delaunay
from numpy import *
from scipy import *
from PIL import *
import homography
import homography
import warp
from scipy import ndimage
#仿射扭曲im1到im2的例子
im1 = array(Image.open('jimei/jimei9.jpg').convert('L'))
subplot(141)
title('jimei1')
axis('off')
imshow(im1)
im2 = array(Image.open('jimei/jimei5.jpg').convert('L'))
subplot(142)
title('jimei2')
axis('off')
imshow(im2)
#选定一些目标点,tp是映射目标位置
tp = array([[0,205,205,0],[500,500,300,300],[1,1,1,1]])
im3 = warp.image_in_image(im1,im2,tp)
#figure()
#gray()
subplot(143)
title('change')
#axis('equal')
axis('off')
imshow(im3)
show()
#下面是三角形仿射
# 选定im1角上的一些点
m,n = im1.shape[:2]
fp = array([[0,m,m,0],[0,0,n,n],[1,1,1,1]])
# 第一个三角形
tp2 = tp[:,:3]
fp2 = fp[:,:3]
# 计算 H
H = homography.Haffine_from_points(tp2,fp2)
#计算H,fp映射到tp,其中tp是映射目标位置
#扭曲操作,直接使用Scipy工具包来完成
im1_t = ndimage.affine_transform(im1,H[:2,:2],
(H[0,2],H[1,2]),im2.shape[:2])
#H[:2,:2]是因为仿射仅取H的前两列
# 三角形的alpha
alpha = warp.alpha_for_triangle(tp2,im2.shape[0],im2.shape[1])
im3 = (1-alpha)*im2 + alpha*im1_t
# 第二个三角形
tp2 = tp[:,[0,2,3]]
fp2 = fp[:,[0,2,3]]
# 计算 H
H = homography.Haffine_from_points(tp2,fp2)
im1_t = ndimage.affine_transform(im1,H[:2,:2],
(H[0,2],H[1,2]),im2.shape[:2])
# 三角形的alpha图像
alpha = warp.alpha_for_triangle(tp2,im2.shape[0],im2.shape[1])
im4 = (1-alpha)*im3 + alpha*im1_t
subplot(144)
imshow(im4)
axis('off')
show()
效果图:

将图像放大,发现图一被翻转了。如图所示:

分析:
程序中对图像块应用仿射变换,称为图像扭曲。 三角形仿射变换中,Alpha通道指的是特别的通道(“非彩色”通道),主要是用来保存选区和编辑选区。在图像学中,透明通道也称Alpha通道,代表数字图像中像素点的透明信息。白色的Alpha像素用以定义不透明的彩色像素,而黑色的Alpha定义透明的像素,黑白之间的灰阶则是彩色图片中的半透明部分。在上面代码中为每个三角形都创建了alpha图像,并将所有的图像合并。
注意:

可能会出现上面的问题,这就需要把原来的PCV包中geometry里的warp.py里的import matplotlib.delaunay as md包替换成如下即可。
from scipy.spatial import Delaunay as md
还有需要注意的是,上面的代码运行的环境是python3.7,在python2中print后不需要加括号。
(3)图像配准
概念:
图像配准是对图像进行变换,是变换后的图像能够在常见的坐标系中对齐。配准可以是严格配准,也可以是非严格配准。其目的在于比较或融合针对同一对象在不同条件下获取的图像,例如图像会来自不同的采集设备,取自不同的时间,不同的拍摄视角等等,有时也需要用到针对不同对象的图像配准问题。具体地说,对于一组图像数据集中的两幅图像,通过寻找一种空间变换把一幅图像映射到另一幅图像,使得两图中对应于空间同一位置的点一一对应起来,从而达到信息融合的目的。
方法分类:
-
基于灰度和模板的,这类方法直接采用相关运算等方式计算相关值来寻求最佳匹配位置,模板匹配(Blocking Matching)是根据已知模板图像到另一幅图像中寻找与模板图像相似的子图像。基于灰度的匹配算法也称作相关匹配算法,用空间二维滑动模板进行匹配,不同匹配算法主要体现在相关准则的选择方面。
常用的算法: 平均绝对差算法(MAD)、绝对误差和算法(SAD)、误差平方和算法(SSD)、平均误差平方和算法(MSD)、归一化积相关算法(NCC)、序贯相似性检测算法(SSDA)、hadamard变换算法(SATD)、局部灰度值编码算法、PIU。 -
基于特征的匹配方法,首先提取图像的特征,再生成特征描述子,最后根据描述子的相似程度对两幅图像的特征之间进行匹配。图像的特征主要可以分为点、线(边缘)、区域(面)等特征,也可以分为局部特征和全局特征。区域(面)特征提取比较麻烦,耗时,因此主要用点特征和边缘特征。
点特征匹配包括: Harris、Moravec、KLT、Harr-like 、HOG 、LBP、SIFT、SURF、BRIEF、SUSAN、FAST 、CENSUS、FREAK、BRISK、ORB、光流法、A-KAZE等。
边缘特征包括: LoG算子、Robert算子、Sobel算子、Prewitt算子、Canny算子等。 -
基于域变换的方法:采用相位相关(傅里叶-梅林变换)、沃尔什变换、小波等方法。
应用:
- 目标检测
- 模型重建
- 运动估计
- 特征匹配
- 肿瘤检测
- 病变定位
- 血管造影
- 地质勘探
- 航空侦察
配准算法的一般步骤:
- 特征提取
- 特征匹配
- 估计变换模型
- 图像重采样及变换
(1)特征提取:
特征提取是指分别提取两幅图像中共有的图像特征,这种特征是出现在两幅图像中对比列、旋转、平移等变换保持一致性的特征,如线交叉点、物体边缘角点、虚圆闭区域的中心等可提取的特征。特征包括:点、线和面三类。
点特征是最常用的一种图像特征,包括物体边缘点、角点、线交叉点等;根据各特征点的兴趣值将特征点分成几个等级。对不同的目的,特征点的提取应各有不同。点特征包括下面几种算法:
1. Harris算法
受信号处理中相关函数启发,给出与自相关函数相联系的矩阵M,M矩阵的特征值是自相关函数的一阶曲率,如果两个曲率值都高,那么认为该点就是角点,此方法对图像旋转、亮度变化、视觉变化和噪声的影响具有很好的鲁棒性。
2. Susan算法
susan算法使用一个圆形的模板在图像上滑动,将位于圆形模板中心的待检测的像素点称为核心点。假设图像为非纹理,核心点领域被划分为两个区域:其一为亮度值等于(或相似于)核心点亮度的区域,称为核值相似区,其二为亮度值不相似于核心点亮度的区域。
3. Harris-Laplace算法
Harris算子能最稳定地在图像旋转、光照变化、透视变换条件下提取二维平面特征点,但在三维尺度空间中,Harris探测子的重复探测性能不好,不同尺度Harris特征点存在位置误差,Harris探测子不具有尺度和仿射不变性。而三维尺度空间中最稳定高效的特征尺度探测算子是归一化的Laplace算子。Harris-Laplace的特征点具有尺度和旋转不变得特性,且对光照变换和小范围视角变化具有稳定性。
4. SIFT特征点提取
使用DOG filter来建立尺度空间。在尺度空间上提取极值点。
对于二维函数,其泰勒展开式为:
![]()
写成矩阵形式:

写成向量形式:
![]()
其中:![]()
关键点的精确位置就在上式极值点所在位置,对上述式子求导数并令导数为0,则有:
![]()
令:![]()
有:


得: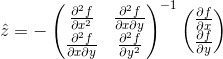
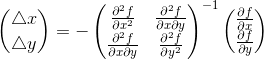
其中f是某一尺度为δ的DoG层。最终得到了△x、△y,即所求极值点相对于关键点的偏移量,若任意一个偏移量超过了0.5,则说明拟合关键点应该在原关键点的相邻位置。在该DoG层不断迭代拟合,确定新关键点位置,直至偏移量都小于0.5(即稳定的关键点)为止。再去除低响应值的点,再删除边缘效应。
5. SURF特征点提取
基于Hessian矩阵,它依靠Hessian矩阵行列式的局部最大值定位兴趣点位置。对于图像I中的某点X在尺度空间上的Hessian矩阵定义为:
![]()
其中
![]() 表示高斯二阶偏导在X处与图像I的卷积。
表示高斯二阶偏导在X处与图像I的卷积。
![]() 具有相似含义。
具有相似含义。
线特征是图像中明显的线段特征,如道路河流的边缘,目标的轮廓线等。线特征的提取一般分两步进行:首先采用某种算法提取出图像中明显的线段信息,然后利用限制条件筛选出满足条件的线段作为线特征。
面特征是指利用图像中明显的区域信息作为特征。在实际的应用中最后可能也是利用区域的重心或圆的圆心点等作为特征。
( 2 ) 特征匹配
特征匹配分两步
a. 对特征作描述
现有的主要特征描述子:SIFT特征描述子,SURF特征描述子,对比度直方图(CCH),DAISY特征描述子,矩方法。
b. 利用相似度准则进行特征匹配
常用的相似性测度准则有如欧式距离,马氏距离,Hausdorff距离等。
SIFT特征描述子:
主要思想:一种基于图像梯度分布的特征描述子。
特点:抗干扰性好,但维数高,计算复杂度大。
SURF特征描述子:
主要思想:将特征点的周围区域分成几个子区域,用每个子区域内像素点的x,y方向的偏导及其绝对值的和组成特征点的描述子。
特点:有较好的抗亮度变化能力,但是该描述子要求使用积分图像,限定了其应用范围。
对比度直方图:
主要思想:将特征点周围区域的像素点与特征点的对比度形成直方图来描述该特征点。
特点:该方法比基于梯度的描述子要快。但描述力比基于梯度的要略弱一点。
DAISY特征描述子:
主要思想:受SIFT算法和GLOH算法的启发,将梯度加权和用几个高斯方向偏导滤波器与原图像进行积分代替。
特点:该描述子有和SIFT特征算子相似的优点,但是速度比SIFT特征算子要快。
(4)图像重采样及变换
在得到两幅图像的变换参数后,要将输入图像做相应参数的变换,使之与参考图像处于同一坐标系下,则矫正后的输入图像与参考图像可用作后续的图像融合、目标变化检测处理或图像镶嵌;
涉及输入图像变换后所得点坐标不一定为整像素数,则应进行插值处理。常用的插值算法有最近领域法,双线性插值法和立方卷积插值法
(三)创建全景图
在同一位置(即图像的照相机位置相同)拍摄的两幅或者多幅图像是单应性相关的,我们可以使用该约束将很多图像缝补起来,拼成一个大的图像来创建全景图。
(1)RANSAC
RANSAC是“RANdom SAmple Consensus”(随机一致性采样)的缩写。其基本思想是,给定点集之间的单应性矩阵,合理的模型应该能够在描述正确数据点的同时摒弃噪声点。
在计算单应性变换矩阵时,只需要四对匹配点,就可以求得两幅图像之间的变换矩阵,然而,在特征点提取时,会产生大量的匹配特征点,这样对变换矩阵H的精度就会有很大的影响,由于在特征检测时特征检测算子对图像特征的误检测,一般的参数估计方法都无法将其排除,所以本文采用RANSAC算法来完成对匹配点的求精。RANSAC算法经常被应用于计算机视觉领域中,是最有效的鲁棒变换估计算法之一,其应用在计算投影变换矩阵的主要步骤为:
- 从两幅图像匹配点集合中随机抽取最少的匹配点集,构成待定投影变换矩阵H的初始模型参数;
- 将所有的集合数据依次代入(1)中所求得的模型中,计算代入点与初始点之间的距离,若小于某一阈值t,则将该点称为内点(inliers),否则称为外点(outliers),将获得的内点进行记录;
- 通过计算获取原始匹配集合中的所有内点(inliers),针对最大inliers集合,用它们重新计算模型参数,即可得到投影变换矩阵H的最终结果。
RANSAC算法的基本假设:
- 数据由“局内点”组成,例如:数据的分布可以用一些模型参数来解释;
- “局外点”是不能适应该模型的数据;(局外点产生的原因有:噪声的极值;错误的测量方法;对数据的错误假设)
- 除此之外的数据属于噪声。
RANSAC算法原理:
OpenCV中滤除误匹配对采用RANSAC算法寻找一个最佳单应性矩阵H,矩阵大小为3×3。RANSAC目的是找到最优的参数矩阵使得满足该矩阵的数据点个数最多,通常令h33=1来归一化矩阵。由于单应性矩阵有8个未知参数,至少需要8个线性方程求解,对应到点位置信息上,一组点对可以列出两个方程,则至少包含4组匹配点对。
s [ x ′ y ′ 1 ] = [ h 11 h 12 h 13 h 21 h 22 h 23 h 31 h 32 h 33 ] [ x y 1 ] s\begin{bmatrix} x'\\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} h_{11} & h_{12}& h_{13}\\ h_{21}& h_{22} &h_{23} \\ h_{31} & h_{32} & h_{33} \end{bmatrix}\begin{bmatrix} x\\ y\\ 1 \end{bmatrix} s⎣⎡x′y′1⎦⎤=⎣⎡h11h21h31h12h22h32h13h23h33⎦⎤⎣⎡xy1⎦⎤其中(x,y)表示目标图像角点位置,(x’,y’)为场景图像角点位置,s为尺度参数。
∑ i = 0 n ( x i ′ − h 11 x i + h 12 y i + h 13 h 31 x i + h 32 y i + h 33 ) 2 + ( y i ′ − h 21 x i + h 22 y i + h 23 h 31 x i + h 32 y i + h 33 ) 2 \sum_{i=0}^{n}({x_{i}}'-\frac{h_{11}x_{i}+h_{12}y_{i}+h_{13}}{h_{31}x_{i}+h_{32}y_{i}+h_{33}})^{2}+({y_{i}}'-\frac{h_{21}x_{i}+h_{22}y_{i}+h_{23}}{h_{31}x_{i}+h_{32}y_{i}+h_{33}})^{2} i=0∑n(xi′−h31xi+h32yi+h33h11xi+h12yi+h13)2+(yi′−h31xi+h32yi+h33h21xi+h22yi+h23)2
RANSAC算法从匹配数据集中随机抽出4个样本并保证这4个样本之间不共线,计算出单应性矩阵,然后利用这个模型测试所有数据,并计算满足这个模型数据点的个数与投影误差(即代价函数),若此模型为最优模型,则对应的代价函数最小。
RANSAC算法的步骤:
- 随机从数据集中随机抽出4个样本数据 (此4个样本之间不能共线),计算出变换矩阵H,记为模型M;
- 计算数据集中所有数据与模型M的投影误差,若误差小于阈值,加入内点集 I;
- 如果当前内点集 I 元素个数大于最优内点集 I_best , 则更新 I_best = I,同时更新迭代次数k :
- 如果迭代次数大于k,则退出 ; 否则迭代次数加1,并重复上述步骤。(注:迭代次数k在不大于最大迭代次数的情况下,是在不断变化的)
k = l o g ( 1 − p ) l o g ( 1 − w m ) k=\frac{log(1-p)}{log(1-w^{m})} k=log(1−wm)log(1−p)
其中,p为置信度,一般取0.995;w为"内点"的比例 ; m为计算模型所需要的最少样本数=4。
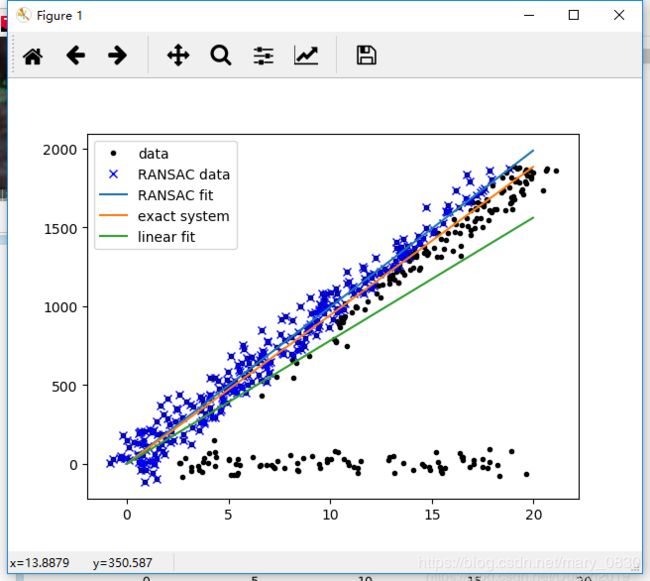
编写实验代码: 用一条直线来拟合包含噪声数据的点集。
# -*- coding: utf-8 -*-
"""
Created on Tue Jun 11 18:39:44 2019
@author: Administrator
"""
import numpy
import scipy # use numpy if scipy unavailable
import scipy.linalg # use numpy if scipy unavailable
def ransac(data, model, n, k, t, d, debug=False, return_all=False):
"""fit model parameters to data using the RANSAC algorithm
This implementation written from pseudocode found at
http://en.wikipedia.org/w/index.php?title=RANSAC&oldid=116358182
{{{
Given:
data - a set of observed data points
model - a model that can be fitted to data points
n - the minimum number of data values required to fit the model
k - the maximum number of iterations allowed in the algorithm
t - a threshold value for determining when a data point fits a model
d - the number of close data values required to assert that a model fits well to data
Return:
bestfit - model parameters which best fit the data (or nil if no good model is found)
iterations = 0
bestfit = nil
besterr = something really large
while iterations < k {
maybeinliers = n randomly selected values from data
maybemodel = model parameters fitted to maybeinliers
alsoinliers = empty set
for every point in data not in maybeinliers {
if point fits maybemodel with an error smaller than t
add point to alsoinliers
}
if the number of elements in alsoinliers is > d {
% this implies that we may have found a good model
% now test how good it is
bettermodel = model parameters fitted to all points in maybeinliers and alsoinliers
thiserr = a measure of how well model fits these points
if thiserr < besterr {
bestfit = bettermodel
besterr = thiserr
}
}
increment iterations
}
return bestfit
}}}
"""
iterations = 0
bestfit = None
besterr = numpy.inf
best_inlier_idxs = None
while iterations < k:
maybe_idxs, test_idxs = random_partition(n, data.shape[0])
maybeinliers = data[maybe_idxs, :]
test_points = data[test_idxs]
maybemodel = model.fit(maybeinliers)
test_err = model.get_error(test_points, maybemodel)
also_idxs = test_idxs[test_err < t] # select indices of rows with accepted points
alsoinliers = data[also_idxs, :]
if debug:
print ('test_err.min()', test_err.min())
print ('test_err.max()', test_err.max())
print ('numpy.mean(test_err)', numpy.mean(test_err))
print ('iteration %d:len(alsoinliers) = %d' % (
iterations, len(alsoinliers)))
if len(alsoinliers) > d:
betterdata = numpy.concatenate((maybeinliers, alsoinliers))
bettermodel = model.fit(betterdata)
better_errs = model.get_error(betterdata, bettermodel)
thiserr = numpy.mean(better_errs)
if thiserr < besterr:
bestfit = bettermodel
besterr = thiserr
best_inlier_idxs = numpy.concatenate((maybe_idxs, also_idxs))
iterations += 1
if bestfit is None:
raise ValueError("did not meet fit acceptance criteria")
if return_all:
return bestfit, {'inliers': best_inlier_idxs}
else:
return bestfit
def random_partition(n, n_data):
"""return n random rows of data (and also the other len(data)-n rows)"""
all_idxs = numpy.arange(n_data)
numpy.random.shuffle(all_idxs)
idxs1 = all_idxs[:n]
idxs2 = all_idxs[n:]
return idxs1, idxs2
class LinearLeastSquaresModel:
"""linear system solved using linear least squares
This class serves as an example that fulfills the model interface
needed by the ransac() function.
"""
def __init__(self, input_columns, output_columns, debug=False):
self.input_columns = input_columns
self.output_columns = output_columns
self.debug = debug
def fit(self, data):
A = numpy.vstack([data[:, i] for i in self.input_columns]).T
B = numpy.vstack([data[:, i] for i in self.output_columns]).T
x, resids, rank, s = numpy.linalg.lstsq(A, B)
return x
def get_error(self, data, model):
A = numpy.vstack([data[:, i] for i in self.input_columns]).T
B = numpy.vstack([data[:, i] for i in self.output_columns]).T
B_fit = scipy.dot(A, model)
err_per_point = numpy.sum((B - B_fit) ** 2, axis=1) # sum squared error per row
return err_per_point
def test():
# generate perfect input data
n_samples = 500
n_inputs = 1
n_outputs = 1
A_exact = 20 * numpy.random.random((n_samples, n_inputs))
perfect_fit = 60 * numpy.random.normal(size=(n_inputs, n_outputs)) # the model
B_exact = scipy.dot(A_exact, perfect_fit)
assert B_exact.shape == (n_samples, n_outputs)
# add a little gaussian noise (linear least squares alone should handle this well)
A_noisy = A_exact + numpy.random.normal(size=A_exact.shape)
B_noisy = B_exact + numpy.random.normal(size=B_exact.shape)
if 1:
# add some outliers
n_outliers = 100
all_idxs = numpy.arange(A_noisy.shape[0])
numpy.random.shuffle(all_idxs)
outlier_idxs = all_idxs[:n_outliers]
non_outlier_idxs = all_idxs[n_outliers:]
A_noisy[outlier_idxs] = 20 * numpy.random.random((n_outliers, n_inputs))
B_noisy[outlier_idxs] = 50 * numpy.random.normal(size=(n_outliers, n_outputs))
# setup model
all_data = numpy.hstack((A_noisy, B_noisy))
input_columns = range(n_inputs) # the first columns of the array
output_columns = [n_inputs + i for i in range(n_outputs)] # the last columns of the array
debug = True
model = LinearLeastSquaresModel(input_columns, output_columns, debug=debug)
linear_fit, resids, rank, s = numpy.linalg.lstsq(all_data[:, input_columns], all_data[:, output_columns])
# run RANSAC algorithm
ransac_fit, ransac_data = ransac(all_data, model,
5, 5000, 7e4, 50, # misc. parameters
debug=debug, return_all=True)
if 1:
import pylab
sort_idxs = numpy.argsort(A_exact[:, 0])
A_col0_sorted = A_exact[sort_idxs] # maintain as rank-2 array
if 1:
pylab.plot(A_noisy[:, 0], B_noisy[:, 0], 'k.', label='data')
pylab.plot(A_noisy[ransac_data['inliers'], 0], B_noisy[ransac_data['inliers'], 0], 'bx',
label='RANSAC data')
else:
pylab.plot(A_noisy[non_outlier_idxs, 0], B_noisy[non_outlier_idxs, 0], 'k.', label='noisy data')
pylab.plot(A_noisy[outlier_idxs, 0], B_noisy[outlier_idxs, 0], 'r.', label='outlier data')
pylab.plot(A_col0_sorted[:, 0],
numpy.dot(A_col0_sorted, ransac_fit)[:, 0],
label='RANSAC fit')
pylab.plot(A_col0_sorted[:, 0],
numpy.dot(A_col0_sorted, perfect_fit)[:, 0],
label='exact system')
pylab.plot(A_col0_sorted[:, 0],
numpy.dot(A_col0_sorted, linear_fit)[:, 0],
label='linear fit')
pylab.legend()
pylab.show()
if __name__ == '__main__':
test()
RANSAC能在有大量噪音情况仍然准确,是因为随机取样时只取一部分可以避免估算结果被离群数据影响。
RANSAC算法的输入为:
- 观测数据 (包括内群与外群的数据)
- 符合部分观测数据的模型 (与内群相符的模型)
- 最少符合模型的内群数量
- 判断数据是否符合模型的阈值 (数据与模型之间的误差容忍度)
- 迭代运算次数 (抽取多少次随机内群)
RANSAC算法的输出为:
- 最符合数据的模型参数 (如果内群数量小于输入第三条则判断为数据不存在此模型)
- 内群集 (符合模型的数据)
RANSAC 算法的优点:
- 鲁棒的估计模型参数
例如,它能从包含大量局外点的数据集中估计出高精度的参数。
RANSAC 算法的缺点:
- 计算参数的迭代次数没有上限
如果设置迭代次数的上限,得到的结果可能不是最优的结果,甚至可能得到错误的结果。RANSAC只有一定的概率得到的可信的模型,概率与迭代次数成正比。
- 要求设置跟问题相关的阈值
RANSAC只能从特定的数据集中估计出一个模型,如果存在两个(或多个)模型,RANSAC不能找到别的模型。(这一部分在homography.py文件中)
(2)稳健的单应性矩阵估计
在任何模型中都可以使用RANSAC模块,在使用RANSAC模块时,只需要在相应Python类中实现fit()和get_error()方法,正确使用ransac.py即可。这里使用可能的对应点集来自动找到用于全景图像的单应性矩阵。
总而言之,就是平面的单应性被定义为一个平面到另外一个平面的投影映射。
通过ransac算法来求解单应性矩阵,调用homegraphy.py中相应函数:
fit() 是计算选取的4个对应的单应性矩阵。
get_error() 是对所有的对应计算单应性矩阵,然后对每个变换后的点,返回相应的误差。
class RansacModel(object):
"""用于测试单应性矩阵的类,其中单应性矩阵是由网站上的ransac.py计算出来的"""
def _init_(self,debug=False):
self.debug = debug
def fit(self,data):
"""计算选取的4个对应的单应性矩阵"""
#该方法仅仅接受由ransac.py选择的4个对应点对,然后拟合一个单应性矩阵。
#将其转置,来调用H_from_points()计算单应性矩阵
data = data.T
#映射的起始点
fp = data[:3,:4]
#映射的目标点
tp = data[3:,:4]
#计算单应性矩阵,然后返回
return H_from_points(fp,tp)
def get_error(self,data,H):
"""对所有的对应计算单应性矩阵,然后对每个变换后的点,返回相应的误差"""
data = data.T
#映射的起始点
fp = data[:3]
#映射的目标点
tp = data[3:]
#变换fp
fp_transformed = dot(H,fp)
#归一化齐次坐标
for i in range(3):
fp_transformed[i]/=fp_transformed[2]
#返回每个点的误差
return sqrt(sum((tp-fp_transformed)**2,axis=0))
#在距离上使用一个阈值来决定哪些单应性矩阵是合理的,该函数允许提供阈值和最小期望的点对数目
def H_from_ransac(fp,tp,model,maxiter=1000,match_theshold=10):
"""使用RANSAC稳健性估计点对应间的单应性矩阵H
#输入:齐次坐标表示的点fp,tp(3*n的数组)"""
import ransac
#对应点组
data = vstack((fp,tp))
#计算H,并返回
H,ransac_data = ransac.ransac(data.T,model,4,maxiter,match_theshold,10,
return_all=True)
return H,ransac_data['inliers']
编写实验代码:
# -*- coding: utf-8 -*-
from pylab import *
from numpy import *
from PIL import Image
import warp
import homography
import sift
imname = ['picture/jimei/jimei' + str(i + 1) + '.jpg' for i in range(8)]
featname = ['picture/jimei/jimei' + str(i + 1) + '.sift' for i in range(8)]
# 提取特征并匹配使用sift算法
l = {}
d = {}
for i in range(5):
sift.process_image(imname[i], featname[i])
l[i], d[i] = sift.read_features_from_file(featname[i])
matches = {}
for i in range(4):
matches[i] = sift.match(d[i + 1], d[i])
实际上,SIFT 是具有很强稳健性的描述子,能够比其他描述子,例如图像块相关的 Harris 角点,产生更少的错误的匹配。但是该方法仍然远非完美。
(3)拼接图像
估计出图像间的单应性矩阵(使用RANSAC算法),现在我们需要将所有的图像扭曲到一个公共的图像平面上。通常,这里的公共平面为中心图像平面。一种方法是创建一个很大的图像,比如图像中全部填充0,使其和中心图像平行,然后将所有的图像扭曲到上面,由于我们所有的图像是由照相机水平旋转拍摄的,因此我们可以使用一个较简单的步骤:将中心图像左边或者右边的区域填充0,以便为扭曲的图像腾出空间。
全景图像拼接步骤:
- 特征点的匹配:
两张图像要能拼接在一起成为一张图像,就需要这两张图像中存在有重合的部分。通过这些重合的部分使用sift特征点匹配的算法,来寻找到重合部分的特征点。需要注意的是,虽然sift算法比Harris角点的效果更好,但是也会出现错误点,并非完美的匹配方法。
合成全景图的第一步是提取并且匹配所有素材图片的局部特征点。
什么是特征点?
普遍来讲,一张图片所包含的特征点通常就是周围含有较大信息量的点,而仅通过这些富有特征的局部,基本就可以推测出整张图片。比如说物体的棱角、夜景闪耀的星星,或是图片里的图案和花纹。
-
图像的匹配:
在找到特征点对之后,因为上文提到sift并非所有匹配点都是正确的,这里我们用到了RANSAC这个方法。这个方法的作用是找到一个合理的模型来描述正确的数据并且尽量忽视噪点的影响。
接下来就是, 找到所有匹配(也就是重叠)的图片部分,连接所有图片之后就可以形成一个基本的全景图了。因为每张图片有可能和其他每张图片有重叠部分,所以匹配全部图片需要差不多匹配图片个数的平方次。不过实际上每两张图片之间只需要那么几个相对精准匹配的点就可以估算出这两张图像里的几何关系。 -
全景图矫直:
矫正拍摄图片时相机的相对3D旋转,主要原因是拍摄图片时相机很可能并不在同一水平线上,并且存在不同程度的倾斜,略过这一步可能导致全景图变成波浪形状。 -
图像均衡补偿:
全局平衡所有图片的光照和色调。 -
图像频段融合:
步骤4之后仍然会存在图像之间衔接边缘、晕影效果(图像的外围部分的亮度或饱和度比中心区域低)、视差效果(因为相机透镜移动导致)。
单应性矩阵是要实现图像拼接重要方法。 它表示了两张图象之间的对应特征点的变换关系。有了这个关系,我们就可以实现图像正确的拼接到另一张图像上。
编写实验代码:
# -*- coding: utf-8 -*-
#coding=utf-8
#RANSAC算法拼接3张图片
from pylab import *
from numpy import *
from PIL import Image
from PCV.geometry import homography, warp
from PCV.localdescriptors import sift
import matplotlib
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=14)
imname = ['picture/home1/' + str(i + 1) + '.jpg' for i in range(4)]
featname = ['picture/home1/' + str(i + 1) + '.sift' for i in range(4)]
l = {}
d = {}
for i in range(4):
sift.process_image(imname[i],featname[i])
l[i],d[i] = sift.read_features_from_file(featname[i])
matches = {}
for i in range(3):
matches[i] = sift.match(d[i+1],d[i])
# visualize the matches (Figure 3-11 in the book)
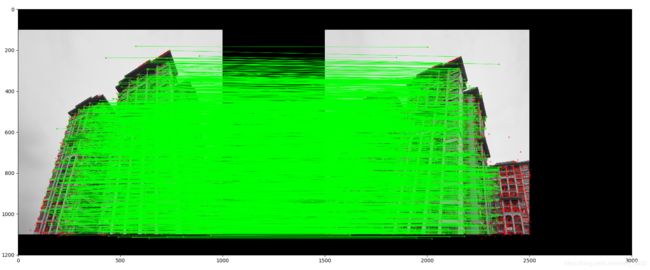
for i in range(3):
im1 = array(Image.open(imname[i]))
im2 = array(Image.open(imname[i+1]))
figure()
sift.plot_matches(im2,im1,l[i+1],l[i],matches[i],show_below=True)
# function to convert the matches to hom. points
def convert_points(j):
ndx = matches[j].nonzero()[0]
fp = homography.make_homog(l[j+1][ndx,:2].T)
ndx2 = [int(matches[j][i]) for i in ndx]
tp = homography.make_homog(l[j][ndx2,:2].T)
# swithh x and y - TODO this should move elsewhere
fp = vstack([fp[1],fp[0],fp[2]])
tp = vstack([tp[1],tp[0],tp[2]])
return fp,tp
# estimate the homographies
model = homography.RansacModel()
fp,tp = convert_points(1)
H_12 = homography.H_from_ransac(fp,tp,model)[0] #im 1 to 2
fp,tp = convert_points(0)
H_01 = homography.H_from_ransac(fp,tp,model)[0] #im 0 to 1
# warp the images
delta = 500 # for padding and translation
im1 = array(Image.open(imname[1]), "uint8")
im2 = array(Image.open(imname[2]), "uint8")
im_12 = warp.panorama(H_12,im1,im2,delta,delta)
im1 = array(Image.open(imname[0]), "f")
im_02 = warp.panorama(dot(H_12,H_01),im1,im_12,delta,delta)
figure()
imshow(array(im_02, "uint8"))
axis('off')
savefig("home1.jpg",dpi=300)
show()
运行结果与分析:
由于没有找到解决方案,因此待我解决了再进行补充。估计是上面的问题影响了整个代码的运行进程,在同学的电脑上可以运行该程序,下面显示该程序的效果图:
经过多次修改调试代码,在博主的电脑上也可以显示出该全景图的绘制。
效果图:
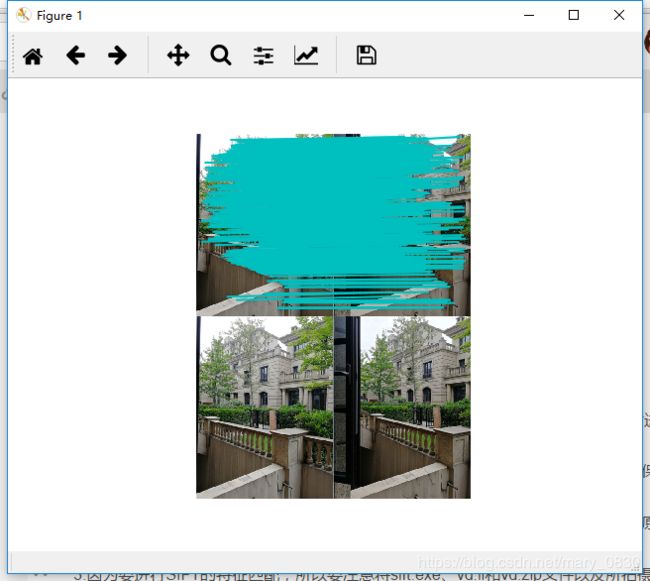


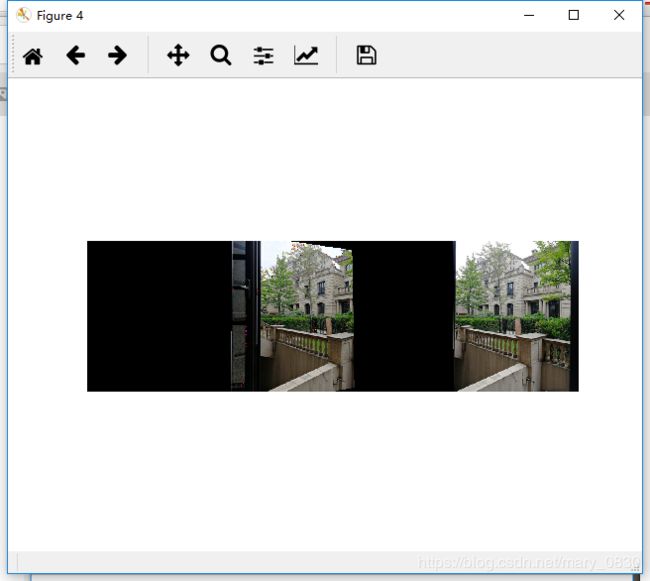
分析:
由于当时想在网上找的图像拼接全景图,但是运行不能成功,因此就拍了一组照片进行拼接,最后的结果是运行成功的。下面说明一些所遇到的问题:
1.图像要能够拼接起来需要在对准同一个物体进行拍摄,从右到左的顺序,使手机保持在同一水平线上拍摄,能够检测出相应的点。
2.拼接图像大小会影响的程序的速度,所以在拍摄图像上传到电脑时候尽量别上传原图,如果上传原图最好能进行压缩。
3.因为要进行SIFT的特征匹配,所以要注意将sift.exe、vd.ll和vd.zip文件以及所拍摄的图像和代码放在同一目录下。
3.发现图像没有能够拼接起来,把整体图像拉长了。
更新:重新进行该实验
第一次实验代码与实验结果
# -*- coding: utf-8 -*-
from pylab import *
from numpy import *
from PIL import Image
from PCV.geometry import homography, warp
from PCV.localdescriptors import sift
import matplotlib
import matplotlib.pyplot as plt
#from matplotlib.font_manager import FontProperties
#font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=14)
imname = [r'D:/Courses/computer vision/test/house' + str(i + 1) + '(1).jpg' for i in range(4)]
# featname = [r'D:/Courses/computer vision/test/house' + str(i + 1) + '.sift' for i in range(5)]
featname = [r'D:/Courses/computer vision/test/out_sift_' + str(i + 1) + '(1).txt' for i in range(4)]
l = {}
d = {}
for i in range(4):
sift.process_image(imname[i],featname[i])
l[i],d[i] = sift.read_features_from_file(featname[i])
matches = {}
for i in range(3):
matches[i] = sift.match(d[i+1],d[i])
# visualize the matches (Figure 3-11 in the book)
for i in range(3):
im1 = array(Image.open(imname[i]))
im2 = array(Image.open(imname[i+1]))
figure()
sift.plot_matches(im2,im1,l[i+1],l[i],matches[i],show_below=True)
# function to convert the matches to hom. points
def convert_points(j):
ndx = matches[j].nonzero()[0]
fp = homography.make_homog(l[j+1][ndx,:2].T)
ndx2 = [int(matches[j][i]) for i in ndx]
tp = homography.make_homog(l[j][ndx2,:2].T)
# swithh x and y - TODO this should move elsewhere
fp = vstack([fp[1],fp[0],fp[2]])
tp = vstack([tp[1],tp[0],tp[2]])
return fp,tp
# estimate the homographies
model = homography.RansacModel()
fp,tp = convert_points(1)
H_12 = homography.H_from_ransac(fp,tp,model)[0] #im 1 to 2
fp,tp = convert_points(0)
H_01 = homography.H_from_ransac(fp,tp,model)[0] #im 0 to 1
#tp,fp = convert_points(2) #NB: reverse order
#H_32 = homography.H_from_ransac(fp,tp,model)[0] #im 3 to 2
#tp,fp = convert_points(2) #NB: reverse order
#H_43 = homography.H_from_ransac(fp,tp,model)[0] #im 4 to 3
# warp the images
delta = 2000 # for padding and translation
im1 = array(Image.open(imname[1]), "uint8")
im2 = array(Image.open(imname[2]), "uint8")
im_12 = warp.panorama(H_12,im1,im2,delta,delta)
im1 = array(Image.open(imname[0]), "f")
im_02 = warp.panorama(dot(H_12,H_01),im1,im_12,delta,delta)
#im1 = array(Image.open(imname[3]), "f")
#im_32 = warp.panorama(H_32,im1,im_02,delta,delta)
#
#im1 = array(Image.open(imname[4]), "f")
#im_42 = warp.panorama(dot(H_32,H_43),im1,im_32,delta,2*delta)
figure()
imshow(array(im_02, "uint8"))
axis('off')
savefig("house.jpg",dpi=300)
show()
实验中遇到的问题:
1.IndexError: index 1019 is out of bounds for axis 0 with size 987

解决方案:检查下面所示的部分有没有是这样的,小白博主之前胡乱修改后就不能报错了。 
2. 可能会遇到这个报错,忽略即可,可以正常运行。 RuntimeWarning: invalid value encountered in less also_idxs = test_idxs[test_err < t] # select indices of
rows with accepted points
说明一下,以上的代码使用的是4张图片进行实验

在代码中中使用其中一部分,如下所示:
如是数据集比较大,可以把后面两段加上。
第二次实验,下面进行两张图片的拼接实验
# -*- coding: utf-8 -*-
import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt
if __name__ == '__main__':
top, bot, left, right = 100, 100, 0, 500
img1 = cv.imread('D:\harris\home1.jpg')
img2 = cv.imread('D:\harris\home2.jpg')
srcImg = cv.copyMakeBorder(img1, top, bot, left, right, cv.BORDER_CONSTANT, value=(0, 0, 0))
testImg = cv.copyMakeBorder(img2, top, bot, left, right, cv.BORDER_CONSTANT, value=(0, 0, 0))
img1gray = cv.cvtColor(srcImg, cv.COLOR_BGR2GRAY)
img2gray = cv.cvtColor(testImg, cv.COLOR_BGR2GRAY)
sift = cv.xfeatures2d_SIFT().create()
# find the keypoints and descriptors with SIFT
kp1, des1 = sift.detectAndCompute(img1gray, None)
kp2, des2 = sift.detectAndCompute(img2gray, None)
# FLANN parameters
FLANN_INDEX_KDTREE = 1
index_params = dict(algorithm=FLANN_INDEX_KDTREE, trees=5)
search_params = dict(checks=50)
flann = cv.FlannBasedMatcher(index_params, search_params)
matches = flann.knnMatch(des1, des2, k=2)
# Need to draw only good matches, so create a mask
matchesMask = [[0, 0] for i in range(len(matches))]
good = []
pts1 = []
pts2 = []
# ratio test as per Lowe's paper
for i, (m, n) in enumerate(matches):
if m.distance < 0.7*n.distance:
good.append(m)
pts2.append(kp2[m.trainIdx].pt)
pts1.append(kp1[m.queryIdx].pt)
matchesMask[i] = [1, 0]
draw_params = dict(matchColor=(0, 255, 0),
singlePointColor=(255, 0, 0),
matchesMask=matchesMask,
flags=0)
img3 = cv.drawMatchesKnn(img1gray, kp1, img2gray, kp2, matches, None, **draw_params)
plt.imshow(img3, ), plt.show()
rows, cols = srcImg.shape[:2]
MIN_MATCH_COUNT = 10
if len(good) > MIN_MATCH_COUNT:
src_pts = np.float32([kp1[m.queryIdx].pt for m in good]).reshape(-1, 1, 2)
dst_pts = np.float32([kp2[m.trainIdx].pt for m in good]).reshape(-1, 1, 2)
M, mask = cv.findHomography(src_pts, dst_pts, cv.RANSAC, 5.0)
warpImg = cv.warpPerspective(testImg, np.array(M), (testImg.shape[1], testImg.shape[0]), flags=cv.WARP_INVERSE_MAP)
for col in range(0, cols):
if srcImg[:, col].any() and warpImg[:, col].any():
left = col
break
for col in range(cols-1, 0, -1):
if srcImg[:, col].any() and warpImg[:, col].any():
right = col
break
res = np.zeros([rows, cols, 3], np.uint8)
for row in range(0, rows):
for col in range(0, cols):
if not srcImg[row, col].any():
res[row, col] = warpImg[row, col]
elif not warpImg[row, col].any():
res[row, col] = srcImg[row, col]
else:
srcImgLen = float(abs(col - left))
testImgLen = float(abs(col - right))
alpha = srcImgLen / (srcImgLen + testImgLen)
res[row, col] = np.clip(srcImg[row, col] * (1-alpha) + warpImg[row, col] * alpha, 0, 255)
# opencv is bgr, matplotlib is rgb
res = cv.cvtColor(res, cv.COLOR_BGR2RGB)
# show the result
plt.figure()
plt.imshow(res)
plt.savefig("pinjie.jpg",dpi=700)
plt.show()
else:
print("Not enough matches are found - {}/{}".format(len(good), MIN_MATCH_COUNT))
matchesMask = None