Python计算机视觉编程第九章——图像分割

（一）图割（Graph Cut）

图论中的图（graph）是由若干节点（有时也称顶点）和连接节点的边构成的集合。边可以是有向的或无向的，并且这些可能有与它们相关联的权重。

图割是将一个有向图分割成两个互不相交的集合，可以用来解决很多计算机视觉方面的问题，诸如立体深度重建、图像拼接和图像分割等计算机视觉方面的不同问题。

从图像像素和像素的近邻创建一个图并引入一个能量或“代价”函数，我们有可能利用图割方法将图像分割成两个或多个区域。图割的基本思想是，相似且彼此相近的像素应该划分到同一区域。

图割 C（C 是图中所有边的集合）的“代价”函数定义为所有割的边的权重求合相加：
$$E_{cut}=\sum _{(i,j)\subset C}{W}_{ij}$$

$W_{ij}$是图中节点i到节点j的边(i,j)的权重，并且是对割 C 所有的边进行求和。

图割图像分割的思想是用图来表示图像，并对图进行划分以使割代价$E_{cut}$最小。在用图表示图像时，增加两个额外的节点，即源点和汇点；并仅考虑那些将源点和汇点分开的割。

寻找最小割（minimum cut 或 min cut）等同于在源点和汇点间寻找最大流（maximum flow 或 max flow）

1. 最大流不可能大于最小割，因为最大流所有的水流都一定经过最小割那些割边，流过的水流怎么可能比水管容量还大呢？
2. 最大流不可能小于最小割，如果小，那么说明水管容量没有物尽其用，可以继续加大水流。

最大流 ：把有向图看作是水管，容量就是能够通过该水管段最高单位流量。基于此类比，最大流就是从起点到终点所能达到的最高单位流量。

计算最大流：假如顶点s（源点）源源不断有水流出，边的权重代表该边允许通过的最大水流量，请问顶点t（终点）流入的水流量最大是多少？

从源点s到终点t共有3条路径：

1. s -> a -> t （流量被边s -> a限制，最大流量为2）
2. s -> b -> t （流量被边”b -> t”限制，最大流量为3）
3. s -> a -> b-> t （边s -> a的流量已经被s -> a -> t 占满，没有流量）

所以顶点流入的最大流为：
$$2+3=5$$

最小割：最小割就是将图切割为两个部分时，代价最小的割的集合。

计算最小割：以最大流图为例，剪短图中的某几条边，使得不存在从s到t的路径，并且保证所减的边的权重和最小。

剪掉边s->a，b->t，剪完以后如图所示：

图中已不存在从s->t的路径，且所修剪的边的权重和为：
$$2+3=5$$
为所有修剪方式中权重和最小的。这样的修剪称为最小割。

可以观察到，最小割和最大流都为5。

举例：用 python-graph 工具包计算一幅较小的图的最大流 / 最小割

from pygraph.classes.digraph import digraph
from pygraph.algorithms.minmax import maximum_flow

gr = digraph()
gr.add_nodes([0,1,2,3])

gr.add_edge((0,1), wt=4)
gr.add_edge((1,2), wt=3)
gr.add_edge((2,3), wt=5)
gr.add_edge((0,2), wt=3)
gr.add_edge((1,3), wt=4)
flows,cuts = maximum_flow(gr, 0, 3)
print ('flow is:' , flows)
print ('cut is:' , cuts)

创建有 4 个节点的有向图，4 个节点的索引分别 0…3，然后用 add_edge() 增添边并为每条边指定特定的权重。边的权重用来衡量边的最大流容量。以节点 0 为源点、3 为汇点，计算最大流。打印出流和割结果：

上面两个 python 字典包含了流穿过每条边和每个节点的标记：0 是包含图源点的部分，1 是与汇点相连的节点。

1.1 从图像创建图

给定一个邻域结构，我们可以利用图像像素作为节点定义一个图。这里讨论最简单的像素四邻域和两个图像区域（前景和背景）情况。一个四邻域 （4-neighborhood）指一个像素与其正上方、正下方、左边、右边的像素直接相连 。

除了像素节点外，我们还需要两个特定的节点——源点和汇点，来分别代表图像的前景和背景。可以利用一个简单的模型将所有像素与源点、汇点连接起来。

步骤：

1. 每个像素节点都有一个从源点的传入边；
2. 每个像素节点都有一个到汇点的传出边；
3. 每个像素节点都有一条传入边和传出边连接到它的近邻。

为确定边的权重，需要一个能够确定这些像素点之间，像素点与源点、汇点之间边的权重（表示那条边的最大流）的分割模型。

像素 i 与像素 j 之间的边的权重记为 $w_{ij}$，源点到像素 i 的权重记为 $w_{si}$，像素 i 到汇点的权重记为 $w_{it}$。

假定我们已经在前景和背景像素（从同一图像或从其他的图像）上训练出了一个贝叶斯分类器，我们就可以为前景和背景计算概率 $p_F(I_i)$和 $p_B(I_i)$。这里，$I_i$是像素 i 的颜色向量。

$$W_{si}=\frac{P_F(I_i)}{P_F(I_i)+P_B(I_i)}$$$$W_{it}=\frac{P_B(I_i)}{P_F(I_i)+P_B(I_i)}$$$$W_{ij}=k{e}^{-|I_i-I_j{|}^2/\sigma }$$

利用该模型，可以将每个像素和前景及背景（源点和汇点）连接起来，权重等于上面归一化后的概率。$w_{ij}$ 描述了近邻间像素的相似性，相似像素权重趋近于κ，不相似的趋近于0。参数 σ 表征了随着不相似性的增加，指数次幂衰减到 0 的快慢。

创建一个名为 graphcut.py 的文件，将下面从一幅图像创建图的函数写入该文件中：

from pylab import *
from numpy import *

from pygraph.classes.digraph import digraph
from pygraph.algorithms.minmax import maximum_flow

from PCV.classifiers import bayes

""" 
Graph Cut image segmentation using max-flow/min-cut. 
"""


def build_bayes_graph(im, labels, sigma=1e2, kappa=1):
    """ 从像素四邻域建立一个图，前景和背景（前景用 1 标记，背景用 -1 标记，其他的用 0 标记）由 labels 决定，并用朴素贝叶斯分类器建模 """

    m, n = im.shape[:2]

    #每行是一个像素的 RGB 向量
    vim = im.reshape((-1, 3))

    # 前景和背景（RGB）
    foreground = im[labels == 1].reshape((-1, 3))
    background = im[labels == -1].reshape((-1, 3))
    train_data = [foreground, background]

    # 训练朴素贝叶斯分类器
    bc = bayes.BayesClassifier()
    bc.train(train_data)

    #  获取所有像素的概率
    bc_lables, prob = bc.classify(vim)
    prob_fg = prob[0]
    prob_bg = prob[1]

    # 用 m * n +2 个节点创建图
    gr = digraph()
    gr.add_nodes(range(m * n + 2))

    source = m * n  # 倒数第二个是源点
    sink = m * n + 1  # 最后一个节点是汇点


    #  归一化
    for i in range(vim.shape[0]):
        vim[i] = vim[i] / (linalg.norm(vim[i]) + 1e-9)

    #  遍历所有的节点，并添加边
    for i in range(m * n):
        # 从源点添加边
        gr.add_edge((source, i), wt=(prob_fg[i] / (prob_fg[i] + prob_bg[i])))

        # 向汇点添加边
        gr.add_edge((i, sink), wt=(prob_bg[i] / (prob_fg[i] + prob_bg[i])))

        #  向相邻节点添加边
        if i % n != 0:  # 左边存在
            edge_wt = kappa * exp(-1.0 * sum((vim[i] - vim[i - 1]) ** 2) / sigma)
            gr.add_edge((i, i - 1), wt=edge_wt)
        if (i + 1) % n != 0:  # 右边存在
            edge_wt = kappa * exp(-1.0 * sum((vim[i] - vim[i + 1]) ** 2) / sigma)
            gr.add_edge((i, i + 1), wt=edge_wt)
        if i // n != 0:  # 上方存在
            edge_wt = kappa * exp(-1.0 * sum((vim[i] - vim[i - n]) ** 2) / sigma)
            gr.add_edge((i, i - n), wt=edge_wt)
        if i // n != m - 1:  # 下方存在
            edge_wt = kappa * exp(-1.0 * sum((vim[i] - vim[i + n]) ** 2) / sigma)
            gr.add_edge((i, i + n), wt=edge_wt)

    return gr

用 1 标记前景训练数据、用 -1 标记背景训练数据的一幅标记图像。 基于这种标记，在 RGB 值上可以训练出一个朴素贝叶斯分类器，然后计算每一像素的分类概率，这些计算出的分类概率便是从源点出来和到汇点去的边的权重；由此可以创建一个节点为n×m+2 的图。注意源点和汇点的索引；为了简化像素的索引，将最后的两个索引作为源点和汇点的索引。

为了在图像上可视化覆盖的标记区域，可以利用 contourf() 函数填充图像（这里指带标记图像）等高线间的区域，参数 alpha 用于设置透明度。将下面函数增加到 graphcut.py 中：

def cut_graph(gr, imsize):
    """    Solve max flow of graph gr and return binary
        labels of the resulting segmentation."""

    m, n = imsize
    source = m * n  # second to last is source
    sink = m * n + 1  # last is sink

    # cut the graph
    flows, cuts = maximum_flow(gr, source, sink)

    # convert graph to image with labels
    res = zeros(m * n)
    for pos, label in cuts.items()[:-2]:  # don't add source/sink
        res[pos] = label

    return res.reshape((m, n))

def save_as_pdf(gr, filename, show_weights=False):
    from pygraph.readwrite.dot import write
    import gv
    dot = write(gr, weighted=show_weights)
    gvv = gv.readstring(dot)
    gv.layout(gvv, 'fdp')
    gv.render(gvv, 'pdf', filename)


def show_labeling(im, labels):
    """    Show image with foreground and background areas.
        labels = 1 for foreground, -1 for background, 0 otherwise."""

    imshow(im)
    contour(labels, [-0.5, 0.5])
    contourf(labels, [-1, -0.5], colors='b', alpha=0.25)
    contourf(labels, [0.5, 1], colors='r', alpha=0.25)
    # axis('off')
    xticks([])
    yticks([])

读取一幅图像， 从图像的两个矩形区域估算出类概率，创建一个图：

# -*- coding: utf-8 -*-
from scipy.misc import imresize
import graphcut
import cv2
import numpy as np
from pylab import  *
from PIL import Image
im = array(Image.open('D:\\Python\\chapter9\\empire.jpg'))
im = imresize(im,0.07,interp='bilinear')
size = im.shape[:2]
# 添加两个矩形训练区域
labels = zeros(size)
labels[3:18,3:18] = -1
labels[-18:-3,-18:-3] = 1
# 创建图
g = graphcut.build_bayes_graph(im,labels,kappa=1)
# 对图进行分割
res = graphcut.cut_graph(g,size)
figure()
graphcut.show_labeling(im,labels)
figure()
imshow(res)
gray()
axis('off')
show()

运行效果如下：

当k=1时，左图为用于模型训练的标记图像，右图为分割的结果：

当k=2，k=5时

分析：
变量 kappa（方程中的K）决定了近邻像素间边的相对权重。观察发现改变K值分割的效果随着 K 值增大，分割边界将变得更平滑，并且细节部分也逐步丢失。

1.2 用户交互式分割

利用一些方法可以将图割分割与用户交互结合起来。例如，用户可以在一幅图像上为前景和背景提供一些标记。另一种方法是利用边界框（bounding box）或“lasso” 工具选择一个包含前景的区域。

编写代码，载入一幅图像及对应的标注信息，然后将其传递到我们的图割分割路径中：

# -*- coding: utf-8 -*-
from scipy.misc import imresize
import graphcut
def create_msr_labels(m,lasso=False):
    """ 从用户的注释中创建用于训练的标记矩阵 """
    labels = zeros(im.shape[:2])
    # 背景
    labels[m==0] = -1
    labels[m==64] = -1
    #前景
    if lasso:
        labels[m == 255] = 1
    else:
        labels[m == 128] = 1
    return labels
    # 载入图像和注释图
    im = array(Image.open('D:\\Python\\chapter9\\images\\37073.jpg'))
    m = array(Image.open('D:\\Python\\chapter9\\images-gt\\37073.png'))
    # 调整大小
    scale = 0.1
    im = imresize(im, scale, interp='bilinear')
    m = imresize(m, scale, interp='nearest')
    # 创建训练标记
    labels = create_msr_labels(m,False)
    # 用注释创建图
    g = graphcut.build_bayes_graph(im, labels, kappa=1)
    # 图割
    res = graphcut.cut_graph(g, im.shape[:2])
    # 去除背景部分
    res[m==0] = 1
    res[m==64] = 1
    # 绘制分割结果
    figure()
    imshow(res)
    gray()
    xticks([])
    yticks([])
   savefig('D:\\Python\\chapter9\\labelplot1.pdf')

代码运行效果如下：

分析：
左边为经过下采样后的原始图像，中间为训练的掩膜，右边为将用RGB像素值作为特征向量进行分割后的结果。观察发现，该算法对于简单图像（一根香蕉，一个小熊玩偶）的分割效果比较好，对于人像的分割，会出现部分模块分割不出来的现象，士兵的裤子和草地颜色相同，帽子和围墙颜色相同，都没有分割出来，但是仅从与背景颜色相似度来说明人像分割不出来，似乎有些没有说服力，因为观察发现香蕉，小熊的左胳膊和右腿都和背景颜色相似且都分割出来了，但是发现它们的背景都是纯色，并没有干扰图像分割的树，围墙，草坪，所以考虑到背景的复杂程度对图像分割可能有一定的影响。同时运行代码发现，图像越复杂，图像分割运行时间也较长。

（二）利用聚类进行分割

基于谱图理论的归一化分割算法，它将像素相似和空间近似结合起来对图像进行分割。

该方法来自定义一个分割损失函数，该损失函数不仅考虑了组的大小而且还用划分的大小对该损失函数进行“归一化”。

$$E_{ncut}=\frac{E_{cut}}{{\sum }_{i\in A}^{}{W}_{ix}}+\frac{E_{cut}}{{\sum }_{j\in B}^{}{W}_{jx}}$$

A 和 B 表示两个割集，并在图中分别对A 和 B 中所有其他节点（函数进行“归一化”这里指图像像素）的权重求和相加，相加求和项称为 association。对于那些像素与其他像素具有相同连接数的图像，它是对划分大小的一种粗糙度量方式。

定义 W 为边的权重矩阵，矩阵中的元素 $w_{ij}$ 为连接像素 i 和像素 j 边的权重。D 为对 W 每行元素求和后构成的对角矩阵，即：
$$D=diag(d_i)$$$$d_i=\sum _j{W}_{ij}$$

归一化分割可以通过最小化下面的优化问题而求得:
$${}_y^{min}\frac{y^T(D-W)y}{y^{T}Dy}$$

向量$y$ 包含的是离散标记，这些离散标记满足对于b 为常数$y_i\in \left\{1,-b\right\}$（即$y$ 只可以取这两个值）的约束，$y^{T}D$求和为 0。由于这些约束条件，该问题不太容易求解 。

然而，通过松弛约束条件并让 $y$ 取任意实数，该问题可以变为一个容易求解的特征分解问题。这样求解的缺点是你需要对输出设定阈值或进行聚类，使它重新成为一个离散分割。

松弛该问题后，该问题便成为求解拉普拉斯矩阵特征向量问题：

$$L=D^{-1/2}W{D}^{-1/2}$$
正如谱聚类情形一样，现在的难点是如何定义像素间边的权重 $w_{ij}$。

我们利用原始归一化割论文中的边的权重，通过下式给出连接像素i 和像素j 的边的权重：
$$w_{ij}=e^{-|I_i-I_j{|}^2/\sigma g}{e}^{-|x_i-x_j{|}^2/\sigma d}$$

式中第一部分度量像素 $I_i$ 和 $I_j$之间的像素相似性，$I_i(I_j)$ 定义为 RGB 向量或灰度值；

第二部分度量图像中 $x_i$ 和 $x_j$ 的接近程度，$x_i(x_j)$ 定义为每个像素的坐标矢量，缩放因子 ${\sigma }_g$ 和 ${\sigma }_d$ 决定了相对尺度和每一部件趋近 0 的快慢。

下面看看这在代码中如何体现，将下面的函数添加到名为 ncut.py 的文件中：

def ncut_graph_matrix(im,sigma_d=1e2,sigma_g=1e-2):
    """  创建用于归一化割的矩阵，其中 sigma_d 和 sigma_g 是像素距离和像素相似性的权重参数 """
    
    m,n = im.shape[:2] 
    N = m*n
    
    # 归一化，并创建 RGB 或灰度特征向量
    if len(im.shape)==3:
        for i in range(3):
            im[:,:,i] = im[:,:,i] / im[:,:,i].max()
        vim = im.reshape((-1,3))
    else:
        im = im / im.max()
        vim = im.flatten()
    
    # x,y 坐标用于距离计算
    xx,yy = meshgrid(range(n),range(m))
    x,y = xx.flatten(),yy.flatten()
    
    # 创建边线权重矩阵
    W = zeros((N,N),'f')
    for i in range(N):
        for j in range(i,N):
            d = (x[i]-x[j])**2 + (y[i]-y[j])**2 
            W[i,j] = W[j,i] = exp(-1.0*sum((vim[i]-vim[j])**2)/sigma_g) * exp(-d/sigma_d)
    
    return W

该函数获取图像数组，并利用输入的彩色图像 RGB 值或灰度图像的灰度值创建一个特征向量。由于边的权重包含了距离部件，对于每个像素的特征向量，我们利用 meshgrid() 函数来获取x 和 y 值，然后该函数会在 N 个像素上循环，并在N×N 归一化割矩阵 W 中填充值。

我们可以顺序分割每个特征向量或获取一些特征向量对它们进行聚类来计算分割结果。这里选择第二种方法，它不需要修改任意分割数也能正常工作。将拉普拉斯矩阵进行特征分解后的前ndim 个特征向量合并在一起构成矩阵W，并对这些像素进行聚类。下面函数实现了该聚类过程：

def cluster(S,k,ndim):
    """ 从相似性矩阵进行谱聚类 """
    
    # 检查对称性
    if sum(abs(S-S.T)) > 1e-10:
        print 'not symmetric'
    
    # 创建拉普拉斯矩阵
    rowsum = sum(abs(S),axis=0)
    D = diag(1 / sqrt(rowsum + 1e-6))
    L = dot(D,dot(S,D))
    
    # 计算 L 的特征向量
    U,sigma,V = linalg.svd(L,full_matrices=False)

    # 从前 ndim 个特征向量创建特征向量
    # 堆叠特征向量作为矩阵的列
    features = array(V[:ndim]).T

    # k-means
    features = whiten(features)
    centroids,distortion = kmeans(features,k)
    code,distance = vq(features,centroids)
        
    return code,V

这里我们采用基于特征向量图像值的 K-means 聚类算法对像素进行分组。现在我们可以利用该算法在一些样本图像上进行测试。下面的脚本展示了一个完整的例子：

# -*- coding: utf-8 -*-
import ncut
import cv2
import numpy as np
from pylab import  *
from PIL import Image
from scipy.misc import imresize
im = array(Image.open('D:\\Python\\chapter9\\empire.jpg'))
m,n = im.shape[:2]
# 调整图像的尺寸大小为 (wid,wid)
wid = 50
rim = imresize(im,(wid,wid),interp='bilinear')
rim = array(rim,'f')
# 创建归一化割矩阵
A = ncut.ncut_graph_matrix(rim,sigma_d=1,sigma_g=1e-2)
# 聚类
code,V = ncut.cluster(A,k=3,ndim=3)
# 变换到原来的图像大小
codeim = imresize(code.reshape(wid,wid),(m,n),interp='nearest')
# 绘制分割结果
figure()
imshow(codeim)
gray()
show()

因为 Numpy 的 linanlg.svd() 函数在处理大型矩阵时的计算速度并不够快（有时对于太大的矩阵甚至会给出不准确的结果），所以这里我们重新设定图像为一固定尺寸（在该例中为 50×50），以便更快地计算特征向量。在重新设定图像大小的时候我们采用了双线性插值法；因为不想插入类标记，所以在重新调整分割结果标记图像的尺寸时我们采用近邻插值法。注意，重新调整到原图像尺寸大小后第一次利用 reshape 方法将一维矩阵变换为（wid，wid）二维数组。



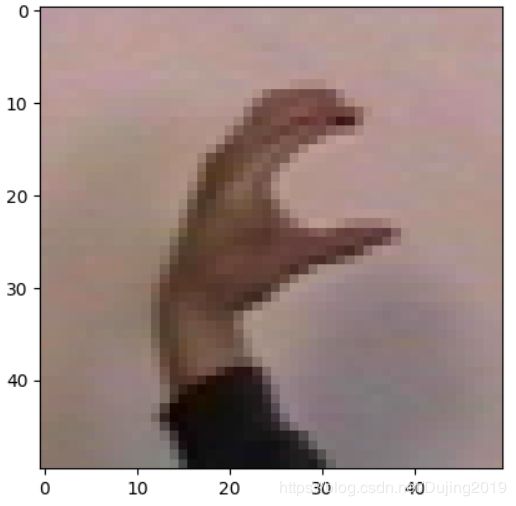
分析：
观察发现，这个分割效果应该是比用户交互式分割效果更差，人像分割不出来，简单图像分割也会有锯齿状，考虑到采用基于特征向量图像值的 K-means 聚类算法对像素进行分组，所以调整过多次k值，依旧不理想，说明选一个合适的k值难度也比较大，运行时间比用户交互式分割方法快一些，不排除是由于降低了分割的精度，分割不准确，所以运行时间短。

（三）变分法

诸如 ROF 降噪、K-means 和 SVM 的例子，这些都是优化问题。当优化的对象是函数时，该问题称为变分问题，解决这类问题的算法称为变分法。 我们看一个简单而有效的变分模型。

下面看一个简单而有效的变分模型。Chan-Vese 分割模型对于待分割图像区域假定一个分片常数图像模型。这里我们集中关注两个区域的情形，比如前景和背景，不过这个模型也可以拓展到多区域。

如果我们用一组曲线$\Gamma$将图像分离成两个区域Ω1 和 Ω2，分割是通过最小化 Chan-Vese 模型能量函数给出的：

$$E(\Gamma )=\lambda length(\Gamma )+{\int }_{\Omega 1}^{}(I-c_1{)}^{2}dx+{\int }_{\Omega 2}^{}(I-c_2{)}^{2}dx$$

该能量函数用来度量与内部平均灰度常数 c1 和外部平均灰度常数 c2 的偏差。这里这两个积分是对各自区域的积分，分离曲线 $\Gamma$ 的长度用以选择更平滑的方案。

import rof
im = array(Image.open('D:\\Python\\chapter9\\ceramic-houses_t0.png').convert("L"))
U,T = rof.denoise(im,im,tolerance=0.001)
t = 0.4 # 阈值
import scipy.misc
scipy.misc.imsave('D:\\Python\\chapter9\\result.pdf',U < t*U.max())

分析：
左图为原始图像，右图为分割后结果，经过对比发现，该算法应该是三个算法中最优秀的，用户交互式分割算法不能处理好复杂背景图像的分割，而该算法能分割出树叶从中的小花，对于前两个算法都不能处理好的人像，该算法也能大致分割出来，对于运行时间，也是三个算法中用时最短，运行最快的。