Slater条件理解和证明
考虑凸优化问题:
min f 0 ( x ) s . t . f i ( x ) ≤ 0 , i = 1 , . . . , k g i ( x ) ≤ 0 , i = 1 , . . . , m \begin{aligned} &\quad \min f_0(x) &\,\\ &\quad s.t.\,\,\,\, f_i(x) \le 0,i=1,...,k\\ &\qquad \,\,\,\,\,\, g_i(x) \le 0,i=1,...,m \end{aligned} minf0(x)s.t.fi(x)≤0,i=1,...,kgi(x)≤0,i=1,...,m
其中 f i f_i fi是凸函数, g g g是仿射函数(等式仿射约束可以转化为两个仿射不等式约束)
Slater条件:如果存在一个 x ~ ∈ r e l i n t D ( 定 义 域 相 对 内 部 ) \tilde{x} \in relint\, \mathcal{D}(定义域相对内部) x~∈relintD(定义域相对内部),使得
f i ( x ) < 0 , i = 1 , ⋯ k , g j ( x ) ≤ 0 , j = 1 , ⋯ , m f_i(x) <0,i=1,\cdots k,g_j(x)\le 0,j=1,\cdots,m fi(x)<0,i=1,⋯k,gj(x)≤0,j=1,⋯,m
则强对偶成立
先贴一个Stephen Boyd凸优化上的简化证明

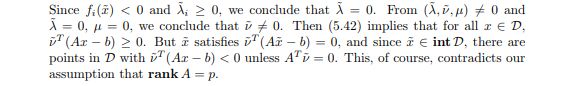
这个证明做了如下的简化:第一,优化目标没有仿射不等式约束;第二,假设内部非空,而
Slater条件只假设点在相对内部中;第三,假设仿射等式约束中 A A A行满秩
第三个简化是无关紧要的,只不过做了这个假设后证明简单
A A A行满秩的假设可以去掉,只需要证明如果不是行满秩(存在冗余等式),那么可以通过一个线性变换,使得约束行满秩,且经过变换之后Lagrange函数的最优值不变,即强对偶性不变
而第一和第二是属于条件的变化,放宽了条件,使得它适用范围更窄
如果不存在仿射约束,有一个简单的证明:见简化版Slater条件证明
如果不存在仿射不等式约束,相对内点这个条件可以去掉
相对内点这个假设的作用在于,仿射函数 h h h如果在一个凸集上C的一个相对内点的值为0,那么它在这个凸集上的值要么为恒值0,要么有正也有负
证:设 f ( a ) = 0 f(a)= 0 f(a)=0, f ( b ) > 0 f(b) > 0 f(b)>0,(<0同理)
则 a a a存在一个邻域 U U U,使得 V = U ∩ C V=U\cap C V=U∩C是吸收的,
当 r > 0 r>0 r>0足够大的时候, a + b − a r ∈ V a+\frac{b-a}{r} \in V a+rb−a∈V,这时候 a − b − a r ∈ V a-\frac{b-a}{r}\in V a−rb−a∈V,
f ( a − b − a r ) = − 1 r f ( b ) < 0 f(a-\frac{b-a}{r}) = -\frac{1}{r}f(b)<0 f(a−rb−a)=−r1f(b)<0
证毕
要完整的证明,但靠书上的分离定理是不够的,需要一个加强版的分离定理
正常分离定理:设 A , B A,B A,B为两个非空凸集, A A A为多面体(多个半平面的交),则存在一个超平面 H H H分离 A , B A,B A,B,且 H H H不包含 B B B的充分必要条件是 A ∩ r e l i n t B = ∅ A \cap relint \,B=\varnothing A∩relintB=∅
利用这个定理可以证明

利用上面的定理就可以证明Slater条件
考虑最前面的优化问题,定义 α \alpha α为其最优值,则由 α \alpha α的定义,不等式组
f 0 ( x ) − α < 0 , f i ( x ) < 0 , g j ( x ) ≤ 0 f_0(x) - \alpha < 0,f_i(x)<0,g_j(x)\le0 f0(x)−α<0,fi(x)<0,gj(x)≤0
无解
由上面定理知道,存在非负实数 λ 0 , ⋯ , λ k , ν 1 , ⋯ , ν m \lambda_0,\cdots,\lambda_k,\nu_1,\cdots,\nu_m λ0,⋯,λk,ν1,⋯,νm且某个 λ i > 0 , \lambda_i>0, λi>0,使得
λ 0 ( f 0 ( x ) − α ) + ⋯ + λ k f k ( x ) + ν 1 g 1 ( x ) + ⋯ ν m g m ( x ) ≥ 0 , ∀ x ∈ D ( ∗ ) \lambda_0(f_0(x)-\alpha)+\cdots+\lambda_kf_k(x)+\nu_1 g_1(x) +\cdots \nu_mg_m(x) \ge 0,\forall x\in \mathcal{D} \quad (*) λ0(f0(x)−α)+⋯+λkfk(x)+ν1g1(x)+⋯νmgm(x)≥0,∀x∈D(∗)
首先 λ 0 > 0 \lambda_0>0 λ0>0,否则的话,设其为0,则某个 λ t > 0 , t > 0 \lambda_t >0,t>0 λt>0,t>0,
由条件存在一个 x ~ ∈ r e i n t D \tilde{x} \in reint \, \mathcal{D} x~∈reintD(这里相对内部不是必要的,相对内部在上面的不等式的证明中才是必要的 )使得 f i < 0 , g i ≤ 0 f_i<0,g_i\le0 fi<0,gi≤0得到
λ 1 f 1 ( x ~ ) + ⋯ + λ k f k ( x ~ ) + ν 1 g 1 ( x ~ ) + ⋯ ν m g m ( x ~ ) = λ 1 f 1 ( x ~ ) + ⋯ + λ k f k ( x ~ ) < 0 \lambda_1 f_1(\tilde{x} )+\cdots+\lambda_kf_k(\tilde{x} )+\nu_1 g_1(\tilde{x} ) +\cdots \nu_mg_m(\tilde{x} ) = \lambda_1 f_1(\tilde{x} )+\cdots+\lambda_kf_k(\tilde{x} ) < 0 λ1f1(x~)+⋯+λkfk(x~)+ν1g1(x~)+⋯νmgm(x~)=λ1f1(x~)+⋯+λkfk(x~)<0
产生矛盾
所以 λ 0 > 0 \lambda_0 > 0 λ0>0,不妨设其为1,(两边除以 λ 0 \lambda_0 λ0),设
h ( x ) = f 0 ( x ) + ⋯ + λ k f k ( x ) + ν 1 g 1 ( x ) + ⋯ ν m g m ( x ) h(x)=f_0(x)+\cdots+\lambda_kf_k(x)+\nu_1 g_1(x) +\cdots \nu_mg_m(x) h(x)=f0(x)+⋯+λkfk(x)+ν1g1(x)+⋯νmgm(x)
由上知 h ( x ) ≥ α , ∀ x ∈ D h(x) \ge \alpha,\forall x\in \mathcal{D} h(x)≥α,∀x∈D,故
inf x ∈ D h ( x ) ≥ α \inf_{x\in \mathcal{D}} h(x)\ge \alpha x∈Dinfh(x)≥α
而对于任意可行解,有 h ( x ) ≤ f 0 ( x ) h(x) \le f_0(x) h(x)≤f0(x),因此
inf x ∈ D h ( x ) = α \inf_{x\in \mathcal{D}} h(x) = \alpha x∈Dinfh(x)=α
即Lagrange 函数 g ( λ , ν ) g(\lambda,\nu) g(λ,ν)在 λ 1 , ⋯ λ k , ν 1 , ⋯ , ν m \lambda_1,\cdots \lambda_k,\nu_1,\cdots,\nu_m λ1,⋯λk,ν1,⋯,νm点取到最大值,且等于原问题最小值,也就是强对偶成立
证毕
参考:Convex Analysis