【DL】卷积_AlexNet
卷积神经网络_AlexNet
- AlexNet特点
- ReLu作为激活函数
- 数据增强
- 层叠池化
- Dropout
- Alex网络结构
- AlexNet的TensorFlow实现
)
由于受到计算机性能的影响,虽然LeNet在图像分类中取得了较好的成绩,但是并没有引起很多的关注。 知道2012年,Alex等人提出的AlexNet网络在ImageNet大赛上以远超第二名的成绩夺冠,卷积神经网络乃至深度学习重新引起了广泛的关注。
AlexNet特点
AlexNet是在LeNet的基础上加深了网络的结构,学习更丰富更高维的图像特征。AlexNet的特点:
- 更深的网络结构
- 使用层叠的卷积层,即卷积层+卷积层+池化层来提取图像的特征
- 使用Dropout抑制过拟合
- 使用数据增强Data Augmentation抑制过拟合
- 使用Relu替换之前的sigmoid的作为激活函数
- 多GPU训练
ReLu作为激活函数
在最初的感知机模型中,输入和输出的关系如下:

只是单纯的线性关系,这样的网络结构有很大的局限性:即使用很多这样结构的网络层叠加,其输出和输入仍然是线性关系,无法处理有非线性关系的输入输出。因此,对每个神经元的输出做个非线性的转换也就是,将上面就加权求和 ∑ i w i x i + b ∑_iw_ix_i+b i∑wixi+b的结果输入到一个非线性函数,也就是激活函数中。 这样,由于激活函数的引入,多个网络层的叠加就不再是单纯的线性变换,而是具有更强的表现能力。
1.sigmoid
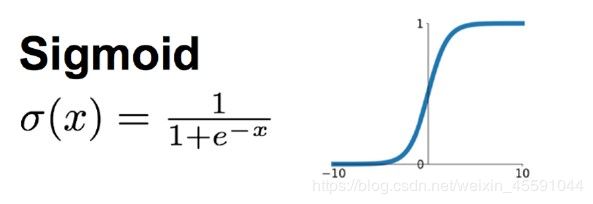
在网络层数较少时,sigmoid函数的特性能够很好的满足激活函数的作用:它把一个实数压缩至0到1之间,当输入的数字非常大的时候,结果会接近1;当输入非常大的负数时,则会得到接近0的结果。这种特性,能够很好的模拟神经元在受刺激后,是否被激活向后传递信息(输出为0,几乎不被激活;输出为1,完全被激活)。
sigmoid一个很大的问题就是梯度饱和。 观察sigmoid函数的曲线,当输入的数字较大(或较小)时,其函数值趋于不变,其导数变的非常的小。这样,在层数很多的的网络结构中,进行反向传播时,由于很多个很小的sigmoid导数累成,导致其结果趋于0,权值更新较慢。
2.ReLu
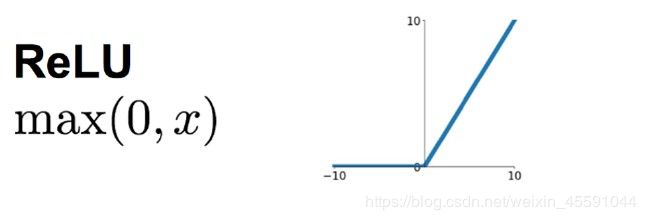
针对sigmoid梯度饱和导致训练收敛慢的问题,在AlexNet中引入了ReLU。ReLU是一个分段线性函数,小于等于0则输出为0;大于0的则恒等输出。相比于sigmoid,ReLU有以下有点:
- 计算开销下。sigmoid的正向传播有指数运算,倒数运算,而ReLu是线性输出;反向传播中,sigmoid有指数运算,而ReLU有输出的部分,导数始终为1.
- 梯度饱和问题
- 稀疏性。Relu会使一部分神经元的输出为0,这样就造成了网络的稀疏性,并且减少了参数的相互依存关系,缓解了过拟合问题的发生。
这里有个问题,前面提到,激活函数要用非线性的,是为了使网络结构有更强的表达的能力。那这里使用ReLU本质上却是个线性的分段函数,是怎么进行非线性变换的。
这里把神经网络看着一个巨大的变换矩阵M,其输入为所有训练样本组成的矩阵A,输出为矩阵B
B = M ⋅ A B=M \cdot A B=M⋅A
这里的M是一个线性变换的话,则所有的训练样本A进行了线性变换输出为B。
那么对于ReLU来说,由于其是分段的,0的部分可以看着神经元没有激活,不同的神经元激活或者不激活,其神经玩过组成的变换矩阵是不一样的。
设有两个训练样本 a1,a2,其训练时神经网络组成的变换矩阵为M1,M2。 由于M1变换对应的神经网络中激活神经元和M2是不一样的,这样M1,M2实际上是两个不同的线性变换。也就是说,每个训练样本使用的线性变换矩阵Mi是不一样的,在整个训练样本空间来说,其经历的是非线性变换。
简单来说,不同训练样本中的同样的特征,在经过神经网络学习时,流经的神经元是不一样的(激活函数值为0的神经元不会被激活)。这样,最终的输出实际上是输入样本的非线性变换。
单个训练样本是线性变换,但是每个训练样本的线性变换是不一样的,这样整个训练样本集来说,就是非线性的变换。
数据增强
神经网络由于训练的参数多,表能能力强,所以需要比较多的数据量,不然很容易过拟合。当训练数据有限时,可以通过一些变换从已有的训练数据集中生成一些新的数据,以快速地扩充训练数据。对于图像数据集来说,可以对图像进行一些形变操作:
- 翻转
- 随机裁剪
- 平移,颜色光照的变换
- …
AlexNet中对数据做了以下操作:
- 随机裁剪,对256×256的图片进行随机裁剪到227×227,然后进行水平翻转。
- 测试的时候,对左上、右上、左下、右下、中间分别做了5次裁剪,然后翻转,共10个裁剪,之后对结果求平均。
- 对RGB空间做PCA(主成分分析),然后对主成分做一个(0, 0.1)的高斯扰动,也就是对颜色、光照作变换,结果使错误率又下降了1%。
层叠池化
在LeNet中池化是不重叠的,即池化的窗口的大小和步长是相等的,如下

在AlexNet中使用的池化(Pooling)却是可重叠的,也就是说,在池化的时候,每次移动的步长小于池化的窗口长度。AlexNet池化的大小为3×3的正方形,每次池化移动步长为2,这样就会出现重叠。重叠池化可以避免过拟合,这个策略贡献了0.3%的Top-5错误率。与非重叠方案s=2,z=2相比,输出的维度是相等的,并且能在一定程度上抑制过拟合。
局部相应归一化
ReLU具有让人满意的特性,它不需要通过输入归一化来防止饱和。如果至少一些训练样本对ReLU产生了正输入,那么那个神经元上将发生学习。然而,我们仍然发现接下来的局部响应归一化有助于泛化。 a x i , y a^i _x,_y axi,y表示神经元激活,通过在(x,y)位置应用核i,然后应用ReLU非线性来计算,响应归一化激活bix,y通过下式给定:
b x , y i = a x , y i / ( k + α ∑ j = m a x ( 0 , i − n / 2 ) m i n ( N − 1 , i + n / 2 ) ( a x , y j ) 2 ) β b^i_{x,y} = a_{x,y}^i / \big( k + \alpha \sum _{j = max(0, i-n / 2)} ^{min(N-1, i+n / 2)} (a_{x,y}^j)^2 \big)^\beta bx,yi=ax,yi/(k+αj=max(0,i−n/2)∑min(N−1,i+n/2)(ax,yj)2)β
其中,N是卷积核的个数,也就是生成的FeatureMap的个数;k,α,β,n是超参数,论文中使用的值是k=2,n=5,α=10−4,β=0.75
输出 b x i , y b^i_x,_y bxi,y和输入 a x j , y a^j_x,_y axj,y的上标表示的是当前值所在的通道,也即是叠加的方向是沿着通道进行。将要归一化的值 a x i , y a^i_x,_y axi,y所在附近通道相同位置的值的平方累加起来 ∑ j = m a x ( 0 , i − n / 2 ) m i n ( N − 1 , i + n / 2 ) ( a x , y j ) 2 \sum ^{min(N-1, i+n / 2)} _{j = max(0, i-n / 2)} (a_{x,y}^j)^2 j=max(0,i−n/2)∑min(N−1,i+n/2)(ax,yj)2
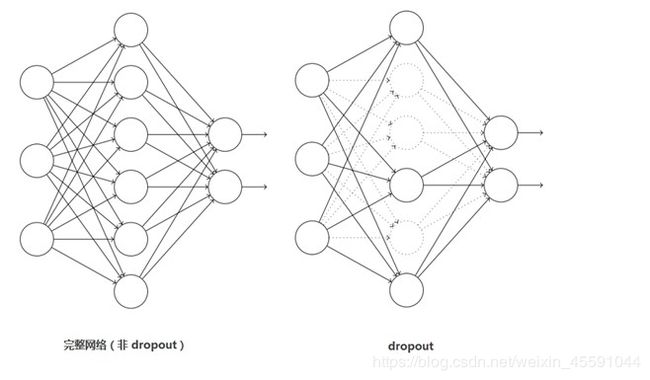
Dropout
这个是比较常用的抑制过拟合的方法了。
引入Dropout主要是为了防止过拟合。在神经网络中Dropout通过修改神经网络本身结构来实现,对于某一层的神经元,通过定义的概率将神经元置为0,这个神经元就不参与前向和后向传播,就如同在网络中被删除了一样,同时保持输入层与输出层神经元的个数不变,然后按照神经网络的学习方法进行参数更新。在下一次迭代中,又重新随机删除一些神经元(置为0),直至训练结束。
Dropout应该算是AlexNet中一个很大的创新,现在神经网络中的必备结构之一。Dropout也可以看成是一种模型组合,每次生成的网络结构都不一样,通过组合多个模型的方式能够有效地减少过拟合,Dropout只需要两倍的训练时间即可实现模型组合(类似取平均)的效果,非常高效。
如下图:
Alex网络结构
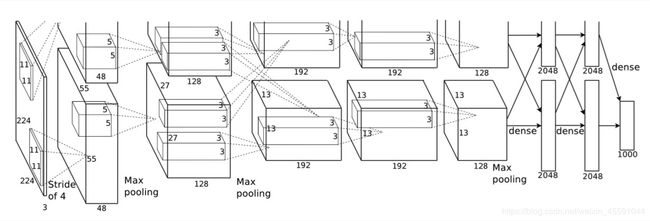
上图中的输入是224×224,不过经过计算(224−11)/4=54.75并不是论文中的55×55,而使用227×227作为输入,则(227−11)/4=55
网络包含8个带权重的层;前5层是卷积层,剩下的3层是全连接层。最后一层全连接层的输出是1000维softmax的输入,softmax会产生1000类标签的分布网络包含8个带权重的层;前5层是卷积层,剩下的3层是全连接层。最后一层全连接层的输出是1000维softmax的输入,softmax会产生1000类标签的分布。
-
卷积层C1
该层的处理流程是: 卷积–>ReLU–>池化–>归一化。
(1) 卷积,输入是227×227,使用96个11×11×3的卷积核,得到的FeatureMap为55×55×96。
ReLU,将卷积层输出的FeatureMap输入到ReLU函数中。
(2) 池化,使用3×3步长为2的池化单元(重叠池化,步长小于池化单元的宽度),输出为27×27×96((55−3)/2+1=27)
(3) 局部响应归一化,使用k=2,n=5,α=10−4,β=0.75进行局部归一化,输出的仍然为27×27×96,输出分为两组,每组的大小为27×27×48 -
卷积层C2
该层的处理流程是:卷积–>ReLU–>池化–>归一化
(1) 卷积,输入是2组27×27×48。使用2组,每组128个尺寸为5×5×48的卷积核,并作了边缘填充padding=2,卷积的步长为1. 则输出的FeatureMap为2组,每组的大小为27×27 times128. ((27+2∗2−5)/1+1=27)
(2) ReLU,将卷积层输出的FeatureMap输入到ReLU函数中
池化运算的尺寸为3×3,步长为2,池化后图像的尺寸为(27−3)/2+1=13,输出为13×13×256
(3) 局部响应归一化,使用k=2,n=5,α=10−4,β=0.75进行局部归一化,输出的仍然为13×13×256,输出分为2组,每组的大小为13×13×128 -
卷积层C3
该层的处理流程是: 卷积–>ReLU
(1)卷积,输入是13×13×256,使用2组共384尺寸为3×3×256的卷积核,做了边缘填充padding=1,卷积的步长为1.则输出的FeatureMap为13×13 times384
(2)ReLU,将卷积层输出的FeatureMap输入到ReLU函数中 -
卷积层C4
该层的处理流程是: 卷积–>ReLU
该层和C3类似。
(1)卷积,输入是13×13×384,分为两组,每组为13×13×192.使用2组,每组192个尺寸为3×3×192的卷积核,做了边缘填充padding=1,卷积的步长为1.则输出的FeatureMap为13×13 times384,分为两组,每组为13×13×192
(2)ReLU,将卷积层输出的FeatureMap输入到ReLU函数中 -
卷积层C5
该层处理流程为:卷积–>ReLU–>池化
(1)卷积,输入为13×13×384,分为两组,每组为13×13×192。使用2组,每组为128尺寸为3×3×192的卷积核,做了边缘填充padding=1,卷积的步长为1.则输出的FeatureMap为13×13×256
(2)ReLU,将卷积层输出的FeatureMap输入到ReLU函数中
池化,池化运算的尺寸为3×3,步长为2,池化后图像的尺寸为 (13−3)/2+1=6,即池化后的输出为6×6×256 -
全连接层FC6
该层的流程为:(卷积)全连接 -->ReLU -->Dropout
(1)卷积->全连接: 输入为6×6×256,该层有4096个卷积核,每个卷积核的大小为6×6×256。由于卷积核的尺寸刚好与待处理特征图(输入)的尺寸相同,即卷积核中的每个系数只与特征图(输入)尺寸的一个像素值相乘,一一对应,因此,该层被称为全连接层。由于卷积核与特征图的尺寸相同,卷积运算后只有一个值,因此,卷积后的像素层尺寸为4096×1×1,即有4096个神经元。
(2)ReLU,这4096个运算结果通过ReLU激活函数生成4096个值
(3)Dropout,抑制过拟合,随机的断开某些神经元的连接或者是不激活某些神经元 -
全连接层FC7
流程为:全连接–>ReLU–>Dropout
(1)全连接,输入为4096的向量
(2)ReLU,这4096个运算结果通过ReLU激活函数生成4096个值
(3)Dropout,抑制过拟合,随机的断开某些神经元的连接或者是不激活某些神经元 -
输出层
第七层输出的4096个数据与第八层的1000个神经元进行全连接,经过训练后输出1000个float型的值,这就是预测结果。
AlexNet参数数量
卷积层的参数 = 卷积核的数量 * 卷积核 + 偏置
C1: 96个11×11×3的卷积核,96×11×11×3+96=34848
C2: 2组,每组128个5×5×48的卷积核,(128×5×5×48+128)×2=307456
C3: 384个3×3×256的卷积核,3×3×256×384+384=885120
C4: 2组,每组192个3×3×192的卷积核,(3×3×192×192+192)×2=663936
C5: 2组,每组128个3×3×192的卷积核,(3×3×192×128+128)×2=442624
FC6: 4096个6×6×256的卷积核,6×6×256×4096+4096=37752832
FC7: 4096∗4096+4096=16781312
output: 4096∗1000=4096000
卷积层 C2,C4,C5中的卷积核只和位于同一GPU的上一层的FeatureMap相连。从上面可以看出,参数大多数集中在全连接层,在卷积层由于权值共享,权值参数较少。
AlexNet的TensorFlow实现
由于AlexNet是使用两块显卡进行训练的,其网络结构的实际是分组进行的。并且,在C2,C4,C5上其卷积核只和上一层的同一个GPU上的卷积核相连。 对于单显卡来说,并不适用,忽略其关于双显卡的的结构,并且将局部归一化操作换成了BN。其网络结构如下:
# -*- coding=UTF-8 -*-
import tensorflow as tf
# 输入数据
import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot=True)
# 定义网络超参数
learning_rate = 0.001
training_iters = 200000
batch_size = 64
display_step = 20
# 定义网络参数
n_input = 784 # 输入的维度
n_classes = 10 # 标签的维度
dropout = 0.8 # Dropout 的概率
# 占位符输入
x = tf.placeholder(tf.types.float32, [None, n_input])
y = tf.placeholder(tf.types.float32, [None, n_classes])
keep_prob = tf.placeholder(tf.types.float32)
# 卷积操作
def conv2d(name, l_input, w, b):
return tf.nn.relu(tf.nn.bias_add( \
tf.nn.conv2d(l_input, w, strides=[1, 1, 1, 1], padding='SAME'),b) \
, name=name)
# 最大下采样操作
def max_pool(name, l_input, k):
return tf.nn.max_pool(l_input, ksize=[1, k, k, 1], \
strides=[1, k, k, 1], padding='SAME', name=name)
# 归一化操作
def norm(name, l_input, lsize=4):
return tf.nn.lrn(l_input, lsize, bias=1.0, alpha=0.001 / 9.0, beta=0.75, name=name)
# 定义整个网络
def alex_net(_X, _weights, _biases, _dropout):
_X = tf.reshape(_X, shape=[-1, 28, 28, 1]) # 向量转为矩阵
# 卷积层
conv1 = conv2d('conv1', _X, _weights['wc1'], _biases['bc1'])
# 下采样层
pool1 = max_pool('pool1', conv1, k=2)
# 归一化层
norm1 = norm('norm1', pool1, lsize=4)
# Dropout
norm1 = tf.nn.dropout(norm1, _dropout)
# 卷积
conv2 = conv2d('conv2', norm1, _weights['wc2'], _biases['bc2'])
# 下采样
pool2 = max_pool('pool2', conv2, k=2)
# 归一化
norm2 = norm('norm2', pool2, lsize=4)
# Dropout
norm2 = tf.nn.dropout(norm2, _dropout)
# 卷积
conv3 = conv2d('conv3', norm2, _weights['wc3'], _biases['bc3'])
# 下采样
pool3 = max_pool('pool3', conv3, k=2)
# 归一化
norm3 = norm('norm3', pool3, lsize=4)
# Dropout
norm3 = tf.nn.dropout(norm3, _dropout)
# 全连接层,先把特征图转为向量
dense1 = tf.reshape(norm3, [-1, _weights['wd1'].get_shape().as_list()[0]])
dense1 = tf.nn.relu(tf.matmul(dense1, _weights['wd1']) + _biases['bd1'], name='fc1')
# 全连接层
dense2 = tf.nn.relu(tf.matmul(dense1, _weights['wd2']) + _biases['bd2'], name='fc2')
# Relu activation
# 网络输出层
out = tf.matmul(dense2, _weights['out']) + _biases['out']
return out
# 存储所有的网络参数
weights = {
'wc1': tf.Variable(tf.random_normal([3, 3, 1, 64])),
'wc2': tf.Variable(tf.random_normal([3, 3, 64, 128])),
'wc3': tf.Variable(tf.random_normal([3, 3, 128, 256])),
'wd1': tf.Variable(tf.random_normal([4*4*256, 1024])),
'wd2': tf.Variable(tf.random_normal([1024, 1024])),
'out': tf.Variable(tf.random_normal([1024, 10]))
}
biases = {
'bc1': tf.Variable(tf.random_normal([64])),
'bc2': tf.Variable(tf.random_normal([128])),
'bc3': tf.Variable(tf.random_normal([256])),
'bd1': tf.Variable(tf.random_normal([1024])),
'bd2': tf.Variable(tf.random_normal([1024])),
'out': tf.Variable(tf.random_normal([n_classes]))
}
# 构建模型
pred = alex_net(x, weights, biases, keep_prob)
# 定义损失函数和学习步骤
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(pred, y))
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate).minimize(cost)
# 测试网络
correct_pred = tf.equal(tf.argmax(pred,1), tf.argmax(y,1))
accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))
# 初始化所有的共享变量
init = tf.initialize_all_variables()
# 开启一个训练
with tf.Session() as sess:
sess.run(init)
step = 1
# Keep training until reach max iterations
while step * batch_size < training_iters:
batch_xs, batch_ys = mnist.train.next_batch(batch_size)
# 获取批数据
sess.run(optimizer, feed_dict={x: batch_xs, y: batch_ys, keep_prob: dropout})
if step % display_step == 0:
# 计算精度
acc = sess.run(accuracy, feed_dict={x: batch_xs, y: batch_ys, keep_prob: 1.})
# 计算损失值
loss = sess.run(cost, feed_dict={x: batch_xs, y: batch_ys, keep_prob: 1.})
print "Iter " + str(step*batch_size) + ", Minibatch Loss= " + "{:.6f}".format(loss) + ", Training Accuracy= " + "{:.5f}".format(acc)
step += 1
print "Optimization Finished!"
# 计算测试精度
print "Testing Accuracy:", sess.run(accuracy, feed_dict={x: mnist.test.images[:256], y: mnist.test.labels[:256], keep_prob: 1.})
以上代码忽略了部分卷积层,全连接层使用了特定的权重。
