msckf开山之作学习笔记

论文原文：

Mourikis, Anastasios I., and Stergios I. Roumeliotis. “A multi-state constraint Kalman filter for vision-aided inertial navigation.” Proceedings 2007 IEEE International Conference on Robotics and Automation. IEEE, 2007.

先通读一遍：找主要贡献，解决的问题
本文的主要贡献在于提出一个描述一个静态特征被多个相机帧看到时，这可以在这些相机位姿中形成一个几何约束，作者提出一个测量模型来表达这个约束，而且这种方法的计算量只随着特征数量线性增长。

Abstract

本文提出基于EKF的实时视觉惯性导航算法。本文的主要贡献是提出一个测量模型可以描述当一个静态特征被多个相机所观测到所形成的约束，这个约束不要求EKF的状态向量包含3D特征位置。算法计算量随着特征数量增加而线性增长，在大范围真实环境中可以实现实时的高精度的定位。

1. Introduction

今年来视觉惯性导航得到了学者们的广泛关注，惯性传感器价格便宜，尺寸小，精度高，可以在GPS信号不好或缺失的情况下提供精准的定位。

视觉传感器可以提供丰富的信息来完成精准定位的任务，但是计算量和定位精度之间是一对矛盾。

本文贡献如Abstract所写。

2. Related Work

SLAM中联合优化IMU位姿和视觉路标点的3D位置，SLAM可以利用它们之间的约束，它的缺点在于计算量比较大。

还有一些方法只估计相机位姿，可以保证实时运行，它们是利用特征观测来得到图相对之间的约束。

本文主要不同在于本文的方法可以表达多相机位姿之间的约束。

Pairwise约束维持一个由多个相机位姿组成的状态向量，pairwise的相对位姿测量来源于图像，并被应用在状态更新，它的缺点在于如果一个特征被多个图像记录，那么额外个约束将被丢弃；而且当相同的观测图像被处理来计算估计量时，它们在统计上不是相互独立的。

还有一种方法和本文的方法相似，它直接使用路标点的测量作为多相机位姿的约束，使用它们作为滑窗内连续帧的约束，然后丢弃它们。但是它没有整合惯性测量，而且没有考虑路标点估计和相机轨迹之间的约束，它也没有提供任何状态估计的协方差测量。

VSDF也是维持一个相机位姿组成的滑窗，它是一个混合batch/recursive算法，它利用延时线性来增加线性误差的鲁棒性，并且利用信息矩阵的稀疏性。但是当动态的运动模型可用时，VSDF的计算复杂度最好是特征数量的平方。

对比VSDF，本文的方法也考虑了延时线性并且计算复杂度是特征数量的一次方。通过之间表达多相机之间的几何约束避免了计算负担和pairwise方法的信息缺失；对比SLAM的方法，本文的方法不要求状态向量中包含特征的3D位置，而且依然能够得到最优的估计。总的来说，本文的方法是非常高效、能够实现高精度实时视觉惯性导航的。

3. Estimator Description

算法总体流程

3.1 Structure of the EKF state vector

evolving IMU 状态

^I_G$\overline{q}$表示从{G}到{I}的旋转；^Gp_I和^Gv_I表示{G}坐标系下的IMU位置和速度；b_g和b_a表示陀螺仪和加速计的偏差，是3x1的向量。

IMU误差状态

对于一般情况

对于四元数

也就是

如果在第k个时间步，有N个相机位姿被包含在EKF状态向量当中，此时向量的形式为

对应误差状态为,这是重点需要记忆的

3.2 Propagation

3.2.1 Continuous-time system modeling

IMU状态各个量求导结果如下：

其中^Ga是global帧下的体加速度，

是IMU帧下的旋转速率，

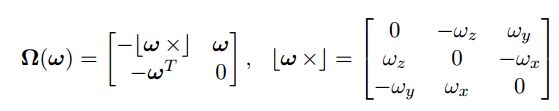
对于里程计和加速计的测量值w_m和a_m满足如下关系：

其中C(.)表示旋转矩阵，n_g和n_a表示零均值高斯白噪声，这里面还考虑了地球旋转角速度w_G，^Gg表示重力加速度。

计算(6)的结果，我们可以得到

这里面我们使用了简洁符号

线性连续时间IMU误差状态模型如下：

其中

表示系统噪声，n_IMU的协方差矩阵Q_IMU是IMU的噪声特性，可以通过标定得到，最后F和G内部如下：


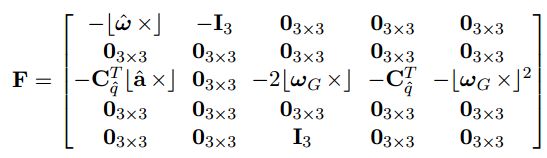
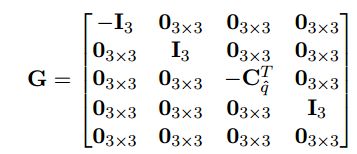
其中I₃表示3x3的单位矩阵。

3.2.2 Discrete-time implementation

IMU样本信号w_m和a_m将在EKF状态传播中被使用，每次得到新的IMU测量，将对(9)使用5阶Runge-Kutta数值积分，而且EKF协方差矩阵也将进行传播，它的形式如下：

其中P_IIk|k表示15 x 15 evolving IMU状态协方差矩阵，P_CCk|k表示 6N x 6N相机位姿估计协方差矩阵，P_ICk|k表示IMU状态和相机估计位姿之间的关联，所有传播状态的协方差矩阵为

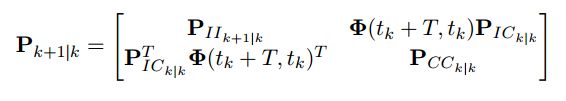
其中P_IIk+1|k是通过Lyapunov的数值积分得到的

数值积分积分的时间范围是(t_k,t_k+T)，初始条件是P_IIk|k。状态转移矩阵的计算也是相似的，是通过以下式子的数值积分得到的

初始条件为：

3.3 State Augmentation

一旦记录了新的图像，相机位姿估计是通过IMU位姿估计计算而来的

其中^C_I$\overline{q}$表示IMU和相机帧之间的旋转四元数；^Ip_C表示{I}坐标系下原始相机帧的位置；前面这两个量都是已知的。当相机位姿估计加入状态向量时，相应的EKF的协方差矩阵也要相应的修改

其中雅克比矩阵J是从(14)得来的

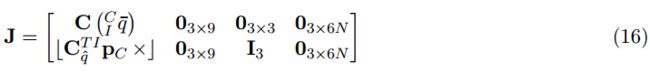
3.4 Measurement Model

文章的主要贡献在此

线性观测模型

其中r表示残差，H表示观测矩阵，noise是零均值的高斯白噪声。

我们基于同一个静态特征被多种位姿的相机观测到这一个约束，对于单个特征f_j，它被一系列的不同位姿(^Ci_G$\overline{q}$, ^Gp_Ci)的相机M_j所观测到，其中i∈S_j。每一个M_j观测到一个特征被以下模型描述：

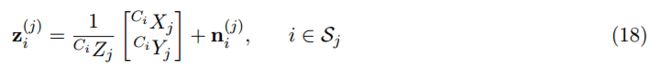
其中n_i是一个2 x 1的图像噪声，它的协方差矩阵为

在相机帧中特征的位置如下：

其中^Gp_fj表示global帧中特征的3D位置，在第一次迭代中它是未知的，我们使用最小二乘法来得到一个估计值^G$p$_fj，这是通过使用测量值z^(j)_i实现的。

一旦估计的特征位置确定，我们就可以计算测量残差

其中

通过将估计位姿和特征位置关系线性化处理，(20)可以近似为

其中H^(j)_Xi和H^(j)_fj是测量z^(j)_i相对于状态和特征位置的雅克比矩阵，而^G$p$_fj表示f_j位置估计的误差，雅克比矩阵结果如下：

以及

其中J^(j)_i是雅克比矩阵

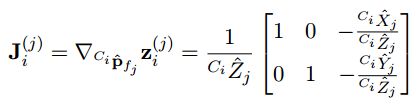
通过将一个特征的所有M_j测量残差堆叠起来，我们可以得到如下表达式

其中r^(j),H^(j)_X,H^(j)_f和n^(j)是所有

向量堆叠起来的矩阵，因为一个特征被不同的图像观测是独立的，因此协方差矩阵n^(j)的协方差为

注意到由于状态估计X被用于计算特征位置估计，特征位置估计的误差^G$p$_fj和误差$X$是有关联的，因此残差r^(j)并不是像(17)那样的形式。为了解决这个问题，我们通过将r^(j)投影到H^(j)_f的左零空间得到r^(j)_o；我们将H_f的左零空间的列形式记为A，我们可以得到

因为2M_j x 3的矩阵H^(j)_f是行满秩的矩阵，它的左零空间的维度为2M_j - 3。因此r^(j)_o是(2M_j-3) x 1的向量。这个残差是独立特征的误差的，因此可以对它使用EKF更新。式(26)记录了观测到特征f_j的所有相机的位姿的线性关联，这个表达式表示了为M_j状态提供的观测z^(j)_i的所有可用的信息，因此EKF更新是最优解，除了线性话带来一定误差外。

其实为了计算残差r^(j)_o和测量矩阵H^(j)_o，A并不需要被精确地估计出来。r的投影，矩阵H^(j)_X和左零空间H^(j)_f可以使用论文[21]中提供的方法搞笑地计算出来，复杂度为O(M²_j)。噪声向量的协方差矩阵如下:

式(25)不是在M_j个图像中观测到静态特征的约束的唯一表示形式。

3.5 EKF Updates

我们现在来讨论EKF更新阶段的细节，在这里从多个特征的观测得到的约束将被使用，它可以被分成两部分

• 当一个特征被跟踪后不在被检测到的时候，所有关于这个特征的测量将根据3.4描述的那样进行处理
• 当一张新的图片被记录时，当前相机位姿估计将被复制并放入状态向量当中。如果达到了所允许的相机位姿的最大值N_max，最老的一个位姿将被移除。

我们现在来讨论细节，首先我们先计算参考向量

以及它对应的测量矩阵

通过这这些向量放在一起，我们可以得到矩阵形式

因为特征测量是相互独立的，噪声向量n^(j)_o相互之间是不相关的，因此噪声向量n_o的协方差矩阵

在实际过程中d可能会非常大，为了减少计算复杂度，我们对H_x使用QR分解

其中Q₁和Q₂是酉矩阵，T_H是上三角矩阵，因此等式(27)可以写成如下形式

通过最后一个式子可以看出，通过将r_o投影到H_x的基向量组成的空间，我们得到了所有测量中有用的信息。残差项Q^T₂r_o是唯一的噪声，可以被完全丢弃，因此我们可以得到更简单的形式

这里面

表示噪声向量，它的协方差矩阵为
R_n = Q^T₁R_oQ₁ = σ²_imI_r
其中r是Q₁的列数，则EKF的卡尔曼增益为：

状态的修正量为

状态的协方差矩阵更新如下

3.6 Discussion

根据以上的讨论，我们发现滤波器的计算复杂度是观测到的特征数量的一次方，状态向量中位姿的数量和滤波器状态向量的长度是可以调整的，以此来适应不同的计算资源。
基于视觉的运动估计对噪声比较敏感，提升算法鲁棒性的两个方法：

• 在测量模型中使用特征的逆深度
• 测量的延时线性化

可以往SLAM方向扩展，进一步提升在长距离情况下的定位精度。

4. Experimental Results

5. Conclusions