多项式回归——自学第七篇
##1、多项式回归
由于之前所讲的线性回归要求数据之间存在线性关系,但是生活中很多的数据不存在线性关系,更多的数据之间是非线性关系,这次采用多项式回归算法(例如 y = a x 2 + b x + c y=ax^{2}+bx+c y=ax2+bx+c)来对非线性数据进行预测。并引出模型泛化相关内容。
如果对于非线性数据进行线性回归,可以得到以下一张图
import numpy as np
import matplotlib.pyplot as plt
x=np.random.uniform(-3,3,size=100)
y=0.5*x**2+x+2+np.random.normal(0,1,size=100)
plt.scatter(x,y,color='r')
plt.show()
from sklearn.linear_model import LinearRegression
x=x.reshape(-1,1)
lin=LinearRegression()
x=x.reshape(-1,1)
lin.fit(x,y)
y_pre=lin.predict(x)
plt.scatter(x,y)
plt.plot(x,y_pre)
plt.show()

可以看到,线性回归无法拟合一个非线性的数据集。
当然如果对拟合时的数据增加一项 x 2 x^{2} x2,再进行predict
##2、sklearn中的多项式回归
多项式回归原理上是对输入的数据的特征进行改变,所以属于数据的预处理部分,所以多项式回归的类在sklearn.preprocessing中
import numpy as np
import matplotlib.pyplot as plt
x=np.random.uniform(-3,3,size=100)
y=0.5*x**2+x+2+np.random.normal(0,1,size=100)
plt.scatter(x,y,color='r')
plt.show()
from sklearn.preprocessing import PolynomialFeatures
poly= PolynomialFeatures(degree=2) #degree是为数据集添加几次幂
X=x.reshape(-1,1)
poly.fit(X,y)
x_poly=poly.transform(X) #实际上是为数据添加了几次幂之后的数据,用于fit和predict
from sklearn.linear_model import LinearRegression
lin=LinearRegression()
lin.fit(x_poly,y)
y_predict=lin.predict(x_poly)
plt.scatter(x,y)
#因为x是随机的,大小不确定,所以绘制曲线的时候不是沿着曲线方向绘制的,
#在这里需要对x进行从小到大排序,并将预测的值y_predict按照排序后的x的索引进行排序
plt.plot(np.sort(x),y_predict[np.argsort(x)],color='r')
plt.show()
print(lin.coef_)
print(lin.intercept_)
[0. 0.90863024 0.44892646]
2.2588967940607496
#第一行输出的是多项式系数(次幂递增),下一行输出的是截距,与刚开始定义的多项式系数和截距相差不大
import numpy as np
import matplotlib.pyplot as plt
x=np.random.uniform(-3,3,size=100)
y=0.5*x**2+x+2+np.random.normal(0,1,size=100)
plt.scatter(x,y,color='r')
plt.show()
from sklearn.preprocessing import PolynomialFeatures
X=x.reshape(-1,1)
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
#Pipeline列表中显示的是管道中的每一个步骤,可以将多步骤合在一起
poly_reg=Pipeline([
("poly",PolynomialFeatures(degree=2)), #多项式实例化
("std_scalar",StandardScaler()) , #数值归一化的实例化
("lin_reg",LinearRegression()) #线性回归
])
poly_reg.fit(X,y)
y_predict=poly_reg.predict(X)
plt.scatter(X,y)
plt.plot(np.sort(x),y_predict[np.argsort(x)],color='r')
plt.show()
##3、过拟合和欠拟合
当多项式的复杂程度越来越高时,很容易发生过拟合现象,其特点是:训练数据拟合结果很好,但是测试数据的拟合结果误差很大,下面我们取degree=100的情况下和普通线性回归的R方误差进行比较。
import numpy as np
import matplotlib.pyplot as plt
x=np.random.uniform(-3,3,size=100)
X=x.reshape(-1,1)
y=0.5*x**2+x+2+np.random.normal(0,1,size=100)
plt.scatter(x,y,color='r')
plt.show()
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
lin=LinearRegression()
lin.fit(X,y)
y_predict=lin.predict(X)
result1=mean_squared_error(y,y_predict)
print(result1)
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
#Pipeline列表中显示的是管道中的每一个步骤,可以将多步骤合在一起
#创建一个多项式回归函数
def polyregression(degree):
return Pipeline([
("poly",PolynomialFeatures(degree=degree)), #多项式实例化
("std_scalar",StandardScaler()) , #数值归一化的实例化
("lin_reg",LinearRegression()) #线性回归
])
polyR=polyregression(degree=100) #实例化管道
polyR.fit(X,y)
y_predict_poly=polyR.predict(X)
result2=mean_squared_error(y,y_predict_poly)
print(result2)
plt.scatter(x,y)
plt.plot(np.sort(x),y_predict_poly[np.argsort(x)],color='r')
plt.show()
R方误差为:
2.213083627265383
0.48887460491580365
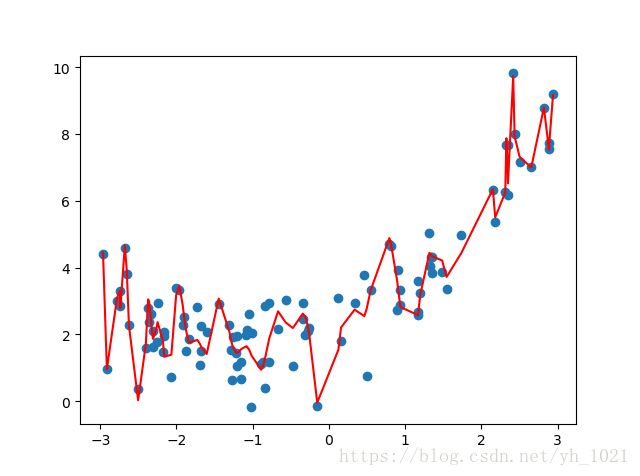
可见degree=100的情况下,曲线很好的拟合了很多的数据点,且R方误差远远小于普通线性回归的误差。但是很明显这不是我们想要的曲线形状,我们把它称之为过拟合,可以说它的泛化能力很差
而当采用线性回归进行拟合时(也就是degree=1时),曲线因太过简单而无法准确拟合数据走势,且R方误差较大,如下图所示,我们把它称之为欠拟合。
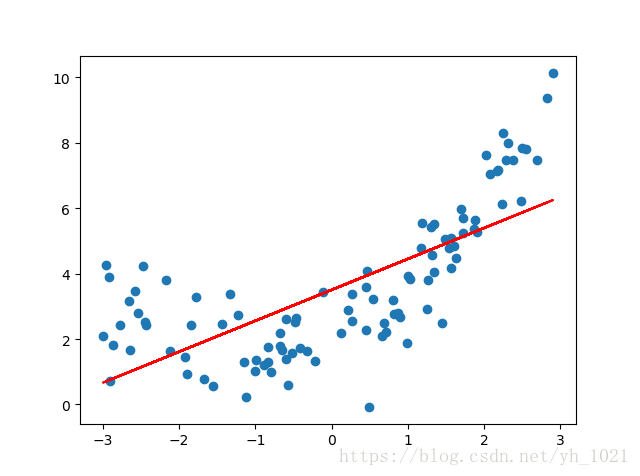
下面我们用均方误差来计算欠拟合和过拟合情况下的误差大小:
import numpy as np
import matplotlib.pyplot as plt
x=np.random.uniform(-3,3,size=100)
X=x.reshape(-1,1)
y=0.5*x**2+x+2+np.random.normal(0,1,size=100)
plt.scatter(x,y,color='r')
plt.show()
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
x_train,x_test,y_train,y_test=train_test_split(X,y,random_state=666)
from sklearn.metrics import mean_squared_error
#测试线性回归的泛化能力
lin1=LinearRegression()
lin1.fit(x_train,y_train)
y_predict=lin1.predict(x_test)
error=mean_squared_error(y_test,y_predict)
print(error)
#测试多项式回归的泛化能力
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
def polyRegression(degree):
return Pipeline([
("poly",PolynomialFeatures(degree=degree)), #多项式实例化
("std_scalar",StandardScaler()) , #数值归一化的实例化
("lin_reg",LinearRegression()) #线性回归
])
poly_reg=polyRegression(degree=20)
poly_reg.fit(x_train,y_train)
y_predict2=poly_reg.predict(x_test)
error2=mean_squared_error(y_test,y_predict2)
print(error2)
输出结果为:
#degree=1(线性回归)(欠拟合)
3.261670749550079
#degree=2
1.0864854974392868
#degree=20(过拟合)
1596.8106492195425
分别绘制训练集和测试集的学习曲线(误差随着训练次数的变化曲线)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
x=np.random.uniform(-3,3,size=100)
y=0.5*x**2+x+2+np.random.normal(0,1,size=100)
plt.scatter(x,y,color='r')
plt.show()
X=x.reshape(-1,1)
y=y.reshape(-1,1)
x_train,x_test,y_train,y_test=train_test_split(X,y,random_state=666)
train_score=[]
test_score=[]
for i in range(1,100):
lin=LinearRegression()
lin.fit(x_train[:i],y_train[:i])
y_train_pre=lin.predict(x_train[:i])
train_score.append(mean_squared_error(y_train_pre,y_train[:i]))
y_test_pre=lin.predict(x_test)
test_score.append(mean_squared_error(y_test_pre,y_test))
plt.plot([i for i in range(1,100)],np.sqrt(train_score),label="train")
plt.plot([i for i in range(1,100)],np.sqrt(test_score),label="test")
plt.axis([0,70,0,4])
plt.legend()
plt.show()

随着训练次数增加,测试集的误差逐渐下降,最终与训练集的误差几乎差不多。
##4、训练——验证——测试
如果训练模型时只分训练数据和测试数据两类,那么当训练的模型用测试数据得到的结果不够好时就会重新训练数据,直到用测试数据测试的结果够好为止。在这个过程中模型似乎是在围绕着这个已知的测试数据不断改善,最终可能发生在这个测试数据上面的过拟合。为了防止这样的情况发生,将数学分为训练——验证——测试三部分,当训练数据训练好了模型后,用验证数据验证,若效果不好改善模型(调整模型超参数)后继续验证,直到验证结果够好的时候再用测试数据进行测试。(训练数据和验证数据都参与了模型的训练,测试数据集没有参与)
##5、交叉验证
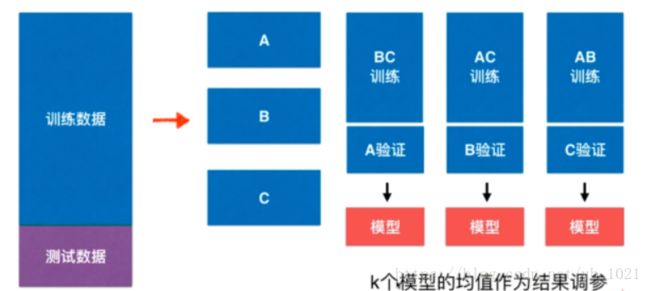
将训练数据集分成n份,每一份都将作为验证集,其余所有的数据作为训练集,这样可以得到n个验证过的模型,再将n个模型的均值作为结果进行调参
或许交叉验证得到的结果会比没有交叉验证得到的结果差一点,但是这也是防止了部分数据的过拟合后的结果,但更具有可信度。
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
digits=datasets.load_digits()
x=digits.data
y=digits.target
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test =train_test_split(x,y,random_state=666)
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import cross_val_score
best_score,best_k,best_p=0,0,0
for k in range(2,11):
for p in range(1,6):
knn=KNeighborsClassifier(weights="distance",n_neighbors=k,p=p)
scores=cross_val_score(knn,x_train,y_train,cv=5)
score=np.mean(scores)
knn.fit(x_train,y_train)
score=knn.score(x_test,y_test)
if score>best_score:
best_score=score
best_k=k
best_p=p
print("Best_k=",best_k)
print("Best_p=",best_p)
print("Best_score=",best_score)
#得到最佳k,p之后,利用该超参数训练自己的模型
best_knn=KNeighborsClassifier(weights="distance",n_neighbors=best_k,p=best_p)
best_knn.fit(x_train,y_train)
final_score=best_knn.score(x_test,y_test)
print(final_score)
#####留一法LOO-CV:
把训练集分成m份(每个数据为一份),这样将完全不受随机的影响,最接近模型真正的性能指标,但是计算量巨大
