支持向量机—SMO论文详解（序列最小最优化算法）

SVM的学习算法可以归结为凸二次规划问题。这样的凸二次规划问题具有全局最优解，并且许多最优化算法可以用来求解，但是当训练样本容量很大时，这些算法往往变得非常低效，以致无法使用。论文《Sequential Minimal Optimization：A Fast Algorithm for Training Support Vector Machines》提出的SMO是针对SVM问题的Lagrange对偶问题开发的高效算法。论文对很多计算细节予以忽略，而网上很多文章的解读要么不详细，要么使用了另外一套符号体系，不方便理解。本文将使用原论文的符号体系进行详细解读。

---

1. 问题概述

支持向量机（SVM）的一大特点是最大化间距（max margin）。对于如上图的二分类问题，虽然有很多线可以将左右两部分分开，但是只有中间的红线效果是最好的，因为它的可活动范围是最大的，从直观上来说，很好理解。
对于线性二分类问题，假设分类面为

u=w⃗ ⋅x⃗ +b(1)

则margin为

m=1∥w∥2(2)

根据max margin规则和约束条件，得到如下优化问题，我们要求的就是参数 w⃗  和 b :

minw⃗ ,b12∥∥w⃗ ∥∥2subjecttoyi(w⃗ ⋅x⃗ i−b)≥1,∀i,(3)

对于正样本，类标号 yi 为+1，反之则为-1。根据拉格朗日对偶，公式（3）可以转换为如下的二次规划（QP）问题，其中 αi 为拉格朗日乘子。

minα⃗ Ψ(α⃗ )=minα⃗ 12∑i=1N∑j=1Nyiyj(xi→,xj→)αiαj−∑i=1Nαi(4)

其中 N 为训练样本的数量，上式需要满足不等式约束：

αi⩾0,∀i(5)

还需要满足等式约束：

∑i=1Nyiαi=0(6)

一旦求解出所有的拉格朗日乘子，则我们可以通过如下的公式得到分类面参数 w⃗  和 b 。

w⃗ =∑i=1Nyiαix⃗ i,b=w⃗ ⋅x⃗ k−ykforsomeαk>0.(7)

当然并不是所有的数据都可以完美的线性可分，可能有少量数据就是混在对方阵营，这时可以通过引入松弛变量 ξi 得到软间隔形式的SVM：

minw⃗ ,b,ξ⃗ 12∥∥w⃗ ∥∥2+C∑i=1Nξisubjecttoyi(w⃗ ⋅x⃗ i−b)≥1−ξi,∀i,(8)

其中的 ξi 为松弛变量，能假装把错的样本分对， C 对max margin和max failures的trade off。对于这个新的优化问题，约束变成了一个box constraint：

0≤αi≤C,∀i(9)

而松弛变量 ξi 不再出现在对偶公式中了。
对于线性不可分的数据，可以用和函数 K 将其投影到高维空间，这样就可分了，由此得到一般的分类面公式：

u=∑j=1NyjαjK(xj→,x⃗ )−b(10)

则最终需要求解的问题如下：

minα⃗ Ψ(α⃗ )=minα⃗ 12∑i=1N∑j=1NyiyjK(xi→,xj→)αiαj−∑i=1Nαi

0≤αi≤C,∀i(11)

∑i=1Nyiαi=0

在这个问题中，变量是拉格朗日乘子，一个变量 αi 对应一个样本点 (xi,yi) ，变量的总数等于样本容量 N 。
KKT条件（Karush-Kuhn-Tucker）是正定二次规划问题有最优解的充分必要条件，其表述如下：

αi=0⇔yiui⩾1,

0<αi<C⇔yiui=1,(12.1)

αi=C⇔yiui≤1.

这里记：输入为训练样本 x⃗ i 时，SVM的输出为 ui ，即：

ui=∑j=1NyjαjK(xj→,xi→)−b(12.2)

2. SMO算法概述

SMO算法是一种启发式算法，其基本思路是：
如果所有变量的解都满足此最优化问题的KKT条件，那么这个最优化问题的解就得到了（因为KKT条件是该最优化问题的充分必要条件）。否则选择两个变量，固定其他的变量，针对这两个问题构建一个二次规划问题。这个二次规划问题的解应该更接近二次规划问题的解（因为这会使得原始二次规划问题的目标函数值更小）。而且，这时子问题可以通过解析方法求解，这样就大大提高了整个算法的计算速度。
每一次，子问题都有两个变量，一个是违反KKT条件最严重的那一个，另一个由约束条件自动确定。如此，SMO算法将原问题不断分解为子问题并对子问题求解，进而得到原问题的最终解。
注意，每个子问题有两个变量，而不能是1个变量，因为当选择一个变量时，由于约束条件，其他变量的值就固定了该变量的值也就固定了。所以子问题中同时更新两个变量。
SMO算法包括两个部分：
（1）求解两个变量二次规划问题的解析方法
（2）选择变量的启发式方法

3 两个变量二次规划问题的求解方法

不失一般性，假设选择的两个变量是 α1 ， α2 ，其他 αi 固定。为了描述方便定义如下符号：

Kij=Kji=K(xi→,xj→)

ui=∑j=1NyjαjoldKji−bold（公式12.2）

vi=∑j=3NyjαjoldKij=ui+bold−y1α1oldK1i−y2α2oldK2i

那么SMO的最优化问题的子问题可以写成：

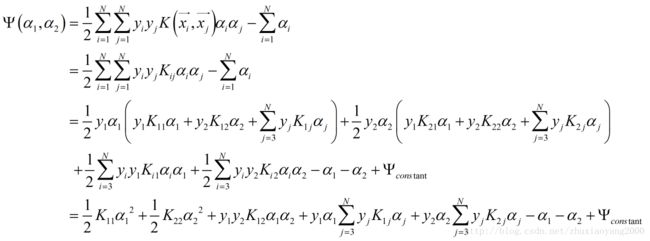
满足约束条件：

α1y1+α2y2=−∑i=3Nαiyi=k

0≤αi≤Ci=1,2

3.1 约束条件

首先，我们分析下约束条件，然后求此约束条件下的极小。
约束条件使得目标函数在一条平行长度为C的正方形的对角线的线段上的最优值。这使得两个变量的最优化问题实质上是单变量的最优化问题，不妨考虑 α2 的最优化问题。
假设初始可行解为 α1old 和 α2old ，最优解为 α1new 和 α2new ，并假设在沿着约束方向未经编辑时的 α2 的最优解为 α2new,unc 。由于 α2new 需要满足不等式约束，所以最优值 α2new 的取值范围必须满足条件：

L≤α2new≤H

当 y1≠y2 时，它们可以表示为

α2=α1+k={k=α2old−α1oldC+k=C+α2old−α1old if α1=0 min value  if α1=C max value 

此时，

L=max(0,α2old−α1old),H=min(C,C+α2old−α1old)(13)

当 y1=y2 时，它们可以表示为

α2=k−α1={k=α2old+α1oldk−C=α2old+α1old−C if α1=0 max value  if α1=C min value 

此时，

L=max(0,α2old+α1old−C),H=min(C,α2old+α1old)(14)

3.2 初步求解 α2

在下面的公式两侧同时乘以 y1

α1y1+α2y2=k

可得

α1+sα2=γ⇒α1=γ−sα2

这里 s=y1y2 ， γ=ky1 为一常数。将上式代入目标函数，可得

Ψ(α2)=12K11(γ−sα2)2+12K22α22+sK12(γ−sα2)α2+y1(γ−sα2)v1−γ+sα2+y2α2v2−α2+Ψconstant

对目标函数求导，可得：

dΨdα2=−sK11(γ−sα2)+K22α2−K12α2+sK12(γ−sα2)−y2v1+s+y2v2−1=0

一般情况下，二次导数为正，这时上式所得 α2 即为所求。
此时，

α2(K11+K22−2K12)=s(K11−K12)γ+y2(v1−v2)+1−s

将 γ=α1+sα2 和 vi 代入上式，即可得：

α2(K11+K22−2K12)=α2old(K11+K22−2K12)+y2(u1−u2+y2−y1)

令： Ei=ui−yi 表示误差项（可以想象，即使分类正确， ui 的值也可能很大）， η=K11+K22−2K12=∥∥Φ(xi)−Φ(xj)∥∥ ，其中 Φ 是原始空间向特征空间的映射，这里 η 可以看成是一个度量两个样本相似性的距离，换句话说，一旦选择核函数则意味着你已经定义了输入空间中元素的相似性。最后得到迭代式：

α2new=α2old+y2(E1−E2)η

3.3 限定 α2 ，并求解 α1

考虑不等式约束条件 L≤α2new≤H ，整理得下式：

α2new,clipped=⎧⎩⎨Lα2newH if α2new⩽L if L<α2new<H if α2new>H

又因为 α1old+sα2old=α1new+sα2new,clipped=γ ，则有

α1new=α1old+s(α2old−α2new,clipped)

。

3.4 更新阈值b

为了使新得到的 α1 和 α2 乘子满足KKT条件，则需要 α1 或 α2 在界内，并满足条件 yiui=1 。
假设 α1new 在界内，则：

y1unew1=1⇒y1(αnew1y1K11+αnew,clipped2y2K21+∑j=3N(αjyjKj1)−bnew)=1

又因为：

E1=u1−y1=αold1y1K11+αold2y2K21+∑j=3N(αjyjKj1)−bold−y1

所以

∑j=3N(αjyjKj1)=E1−αold1y1K11−αold2y2K21+bold+y1

将其代入上式，可得

y1(αnew1y1K11+αnew,clipped2y2K21+E1−αold1y1K11−αold2y2K21+bold+y1−bnew)=1

等式两侧同时乘以 y1 ，可得

bnew1=E1+y1(αnew1−αold1)K11+y2(αnew,clipped2−αold2)K12+bold

同理，假设 α2new,clipped 在界内，则：

bnew2=E2+y1(αnew1−αold1)K12+y2(αnew,clipped2−αold2)K22+bold