约束极值问题之拉格朗日乘子法、KKT条件与对偶理论
文章目录
- 1 等式约束极值问题
- 1.1 拉格朗日乘子法(必要条件)
- 2 不等式约束极值问题
- 2.1 约束作用
- 2.2 不等式约束的几何解释
- 2.3 下降方向
- 2.4 可行方向
- 2.5 Fritz John条件(最优解必要条件)
- 2.6 Kuhn-Tucker条件(最优解必要条件 - 约束规格)
- 2.7 最优解必要条件
- 3 对偶问题
- 3.1 原始问题的等价问题
- 3.2 原始问题的对偶问题
- 3.3 原始问题与对偶问题关系
1 等式约束极值问题
考虑非线性规划
min f ( x ) x ∈ R n s.t. φ i ( x ) = 0 , i = 1 , ⋯ , m \begin{aligned} \min &\quad f({x}) \quad {x}\in\R^n \\ \text{s.t.} &\quad \varphi_i({x}) =0,\quad i=1,\cdots,m \end{aligned} mins.t.f(x)x∈Rnφi(x)=0,i=1,⋯,m
由于自变量的相互独立性被约束条件破坏,不可任意使用求导后的结果。
1.1 拉格朗日乘子法(必要条件)
考虑约束极值问题:求双曲线xy=3离原点最近的点?
min x 2 + y 2 s.t. x y = 3 \begin{aligned} \min &\quad x^2 + y^2 \\ \text{s.t.} &\quad xy=3 \end{aligned} mins.t.x2+y2xy=3
等式约束也可通过变量替换的形式将约束条件加入目标函数,从而转换为无约束极值问题,但一般不易求解。令目标函数 f ( x ) = x 2 + y 2 f(x)=x^2+y^2 f(x)=x2+y2,约束函数 φ ( x ) = x y − 3 = 0 \varphi(x)=xy-3=0 φ(x)=xy−3=0,目标函数的等高线和约束曲线如下:

当目标函数与约束曲面相切时(目标函数的梯度正交于约束曲面),可能取得最优值。当 f ( x ) f(x) f(x)与 φ ( x ) \varphi(x) φ(x)相交时,在等高线 f ( x ) f(x) f(x)的内外侧一定存在更大或更小的等高线(目标值)。相切亦不一定保证是极值点,这与 f ( x ) f(x) f(x)和 φ ( x ) \varphi(x) φ(x)的凹凸性有关。
f f f和 φ \varphi φ在切点处的梯度方向/法方向平行,即满足 ∇ f ( x ) = λ ∇ φ ( x ) \nabla f(x)=\lambda \nabla \varphi(x) ∇f(x)=λ∇φ(x),即 ( 2 x , 2 y ) T = λ ( y , x ) T (2x, 2y)^T=\lambda(y, x)^T (2x,2y)T=λ(y,x)T,因此等式约束问题转换为
{ 2 x = λ y 2 y = λ x x y = 3 \begin{cases} 2x=\lambda y \\ 2y = \lambda x \\ xy = 3 \end{cases} ⎩⎪⎨⎪⎧2x=λy2y=λxxy=3
易求得上述方程的解为 { ( x , y ) ∣ ( − 3 , − 3 ) , ( 3 , 3 ) } \{(x,y)\,|\,(-\sqrt 3, -\sqrt 3), (\sqrt 3, \sqrt 3)\} {(x,y)∣(−3,−3),(3,3)}。
一般性,对于等式约束极值问题,定义辅助拉格朗日函数
L ( x , λ ) = f ( x ) + ∑ i = 1 m λ i φ i ( x ) L(x, \lambda)=f(x) + \sum_{i=1}^m\lambda_i\varphi_i(x) L(x,λ)=f(x)+i=1∑mλiφi(x)
分别对 x x x和 λ \lambda λ求偏导,并令各偏导为0,得
{ ∇ f ( x ) + ∑ i = 1 m λ i ∇ φ i ( x ) = 0 φ i ( x ) = 0 , i = 1 , 2 , ⋯ , m \begin{cases} \nabla f(x) + \sum\limits_{i=1}^m \lambda_i \nabla \varphi_i(x) = 0 \\ \varphi_i(x) = 0, \quad i = 1,2,\cdots,m \end{cases} ⎩⎨⎧∇f(x)+i=1∑mλi∇φi(x)=0φi(x)=0,i=1,2,⋯,m
上述方程组,恰好给出了等式约束和最优解的必要条件。
证明:最优解处目标函数和约束函数法向量平行,以及拉格朗日函数的意义
假设寻求函数
z = f ( x , y ) z=f(x, y) z=f(x,y)在条件
φ ( x , y ) = 0 \varphi(x,y)=0 φ(x,y)=0下的极值的必要条件。
假设 ( x 0 , y 0 ) (x_0, y_0) (x0,y0)处取得极值,首先满足 φ ( x 0 , y 0 ) = 0 \varphi(x_0, y_0)=0 φ(x0,y0)=0。假定 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)的某邻域内 f ( x , y ) f(x,y) f(x,y)和 g ( x , y ) g(x,y) g(x,y)均有一阶连续偏导,且 φ y ( x , y ) ≠ 0 \varphi_y(x,y)\neq 0 φy(x,y)=0。由隐函数存在定理,存在具有连续导数的函数 y = ψ ( x ) y=\psi(x) y=ψ(x)使得
z = f ( x , ψ ( x ) ) z=f(x,\psi(x)) z=f(x,ψ(x))由极值的必要条件,知
d z d x ∣ x = x 0 = f x ( x 0 , y 0 ) + f y ( x 0 , y 0 ) d y d x ∣ x = x 0 = 0 \frac{\mathrm dz}{\mathrm dx}\Big |_{x=x_0}=f_x(x_0,y_0)+f_y(x_0,y_0)\frac{\mathrm dy}{\mathrm dx}\big |_{x=x_0}=0 dxdz∣∣∣x=x0=fx(x0,y0)+fy(x0,y0)dxdy∣∣x=x0=0由隐函数求导公式,知
∂ φ ∂ x + ∂ φ ∂ y d y d x = 0 ⇒ d y d x = − φ x φ y ⇒ d y d x ∣ x = x 0 = − φ x ( x 0 , y 0 ) φ y ( x 0 , y 0 ) \frac{\partial\varphi}{\partial x} + \frac{\partial\varphi}{\partial y}\frac{\mathrm dy}{\mathrm dx}=0 \quad \Rightarrow \quad \frac{\mathrm dy}{\mathrm dx}=-\frac{\varphi_x}{\varphi_y} \quad \Rightarrow \quad \frac{\mathrm dy}{\mathrm dx}\big |_{x=x_0}=-\frac{\varphi_x(x_0,y_0)}{\varphi_y(x_0,y_0)} ∂x∂φ+∂y∂φdxdy=0⇒dxdy=−φyφx⇒dxdy∣∣x=x0=−φy(x0,y0)φx(x0,y0)因此
f x ( x 0 , y 0 ) φ x ( x 0 , y 0 ) = f y ( x 0 , y 0 ) φ y ( x 0 , y 0 ) = − λ \frac{f_x(x_0,y_0)}{\varphi_x(x_0,y_0)}=\frac{f_y(x_0,y_0)}{\varphi_y(x_0,y_0)}=-\lambda φx(x0,y0)fx(x0,y0)=φy(x0,y0)fy(x0,y0)=−λ综上所述,最优解的必要条件
{ f x ( x 0 , y 0 ) + λ φ x ( x 0 , y 0 ) = 0 f y ( x 0 , y 0 ) + λ φ y ( x 0 , y 0 ) = 0 φ ( x 0 , y 0 ) = 0 \begin{cases} f_x(x_0,y_0)+\lambda \varphi_x(x_0,y_0)=0\\ f_y(x_0,y_0)+\lambda \varphi_y(x_0,y_0)=0\\ \varphi(x_0,y_0)=0 \end{cases} ⎩⎪⎨⎪⎧fx(x0,y0)+λφx(x0,y0)=0fy(x0,y0)+λφy(x0,y0)=0φ(x0,y0)=0引入辅助拉格朗日函数 L ( x , y , λ ) = f ( x , y ) + λ φ ( x , y ) L(x,y,\lambda)=f(x,y)+\lambda \varphi(x,y) L(x,y,λ)=f(x,y)+λφ(x,y),令 L ( x , y , λ ) L(x,y,\lambda) L(x,y,λ)对各变量的偏导为0等价于上述方程组。
2 不等式约束极值问题
考虑非线性规划问题
min f ( x ) x ∈ R n s.t. g i ( x ) ≤ 0 , i = 1 , ⋯ , m \begin{aligned} \min &\quad f({x}) \quad {x}\in\R^n\\ \text{s.t.} &\quad g_i({x}) \leq 0,\quad i=1,\cdots,m\\ \end{aligned} mins.t.f(x)x∈Rngi(x)≤0,i=1,⋯,m
可行域 S = { x ∣ g i ( x ) ≤ 0 , i = 1 , 2 , ⋯ , m } S=\{{x}|g_i({x})\leq 0, i=1,2,\cdots,m\} S={x∣gi(x)≤0,i=1,2,⋯,m}。
2.1 约束作用
设 x ∗ x^* x∗上述非线性规划问题的一个可行解,根据可行解的位置,约束作用可分为两种:
- 当 g i ( x ∗ ) = 0 g_i( x^*) = 0 gi(x∗)=0, x ∗ x^* x∗位于 S S S边界, x ∗ x^* x∗变动受到约束,该约束条件是 x ∗ x^* x∗的起作用约束,约束下标集 I = { i ∣ g i ( x ∗ ) = 0 } I = \{i \, | \, g_i(x^*) = 0\} I={i∣gi(x∗)=0},图中A点;
- 当 g i ( x ∗ ) < 0 g_i( x^*) < 0 gi(x∗)<0, x ∗ x^* x∗位于 S S S内部, x ∗ x^* x∗变动不受约束,该约束条件是$ x^*$的不起作用约束,图中B点;

2.2 不等式约束的几何解释
当约束区域 S S S包含目标函数原有可行解时,此时可行解满足 g i ( x ∗ ) < 0 g_i(x^*)<0 gi(x∗)<0,约束不起作用,等价于无约束极值问题;当约束区域 S S S不包含原有可行解时,此时可行解满足 g i ( x ∗ ) = 0 g_i(x^*)=0 gi(x∗)=0,约束起作用,可使用拉格朗日方法求解。
因此可行解位于可行域内部时, λ = 0 \lambda=0 λ=0;可行解位于可行域边界时, g i ( x ∗ ) = 0 g_i(x^*)=0 gi(x∗)=0,因此无论哪种情况,均有
λ g i ( x ∗ ) = 0 \lambda g_i(x^*)=0 λgi(x∗)=0
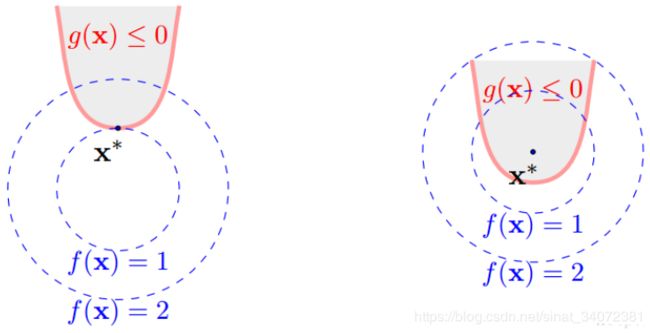
由上图可知,可行解应尽可能靠近约束边界(梯度方向指向边界),目标函数的负梯度方向应朝向无约束时的解(负梯度方向指向圆心极限值点)。对于该非线性规划问题,约束函数的梯度方向与目标函数的负梯度方向同向:
− ∇ f ( x ) = λ ∇ g i ( x ) , λ > 0 -\nabla f(x)=\lambda \nabla g_i(x), \quad \lambda > 0 −∇f(x)=λ∇gi(x),λ>0
梯度的方向
对于线性规划中的约束条件 g i ( x ∗ ) ≤ 0 g_i(x^*)\leq0 gi(x∗)≤0,可行域对应图3中的红色区域。由于梯度是函数增长的方向,可行域的边界值为0,内部值小于0,因此可行域内某点的梯度方向指向可行域边界(较大的函数值)。
注:若可行域为 g i ( x ∗ ) ≥ 0 g_i(x^*)\geq0 gi(x∗)≥0,则可行域内某点的梯度方向指向可行域中心。
2.3 下降方向
设 x ∗ ∈ R n x^* \in \R^n x∗∈Rn, d {d} d是非零向量,若 ∃ δ \exists \delta ∃δ使得每个 λ ∈ ( 0 , δ ) \lambda \in (0, \delta) λ∈(0,δ),都有 f ( x ∗ + λ d ) < f ( x ∗ ) f(x^* + \lambda {d})
2.4 可行方向
设 x ∗ x^* x∗为可行解, d {d} d是非零向量,若 ∃ δ \exists \delta ∃δ使得每个 λ ∈ ( 0 , δ ) \lambda \in (0, \delta) λ∈(0,δ),都有 x ∗ + λ d ∈ S x^* + \lambda {d}\in S x∗+λd∈S,则称 d {d} d为 x ∗ x^* x∗处的可行方向。 D = { d ∣ d ≠ 0 , x ∗ ∈ cl S , ∃ δ > 0 , ∀ λ ∈ ( 0 , δ ) , x ∗ + λ d ∈ S } D= \{{d}|{d}\neq 0, x^* \in \text{cl S}, \exists \delta > 0, \forall \lambda \in (0, \delta), x^*+\lambda {d} \in S\} D={d∣d=0,x∗∈cl S,∃δ>0,∀λ∈(0,δ),x∗+λd∈S},则称为 x ∗ x^* x∗处的可行方向锥。
设 x ∗ x^* x∗为可行解, d {d} d是非零向量,对于 x ∗ x^* x∗的所有起作用约束,若 ∃ δ \exists \delta ∃δ使得每个 λ ∈ ( 0 , δ ) \lambda \in (0, \delta) λ∈(0,δ),都有 g i ( x ∗ + λ d ) < 0 g_i( x^* +\lambda d) < 0 gi(x∗+λd)<0,即
g i ( x ∗ + λ d ) ≈ g i ( x ∗ ) + ∇ g i ( x ∗ ) T d = ∇ g i ( x ∗ ) T d < 0 , i ∈ I g_i( x^* +\lambda d) \approx g_i(x^*)+ \nabla g_i(x^*)^T d = \nabla g_i(x^*)^T d < 0, \quad i \in I gi(x∗+λd)≈gi(x∗)+∇gi(x∗)Td=∇gi(x∗)Td<0,i∈I
即当 i ∈ I i\in I i∈I,只要满足 ∇ g i ( x ∗ ) T d < 0 \nabla g_i( x^*)^T{d} < 0 ∇gi(x∗)Td<0,则 g i ( x ∗ + λ d ) < 0 g_i( x^* +\lambda d)< 0 gi(x∗+λd)<0,即 d d d为 x ∗ x^* x∗的可行方向。
2.5 Fritz John条件(最优解必要条件)
由下降方向和可行方向的定义可知,若$ x^ 是 最 优 解 , 则 ∗ ∗ 是最优解,则 ** 是最优解,则∗∗ x^ 处 , 约 束 函 数 处,约束函数 处,约束函数g 的 可 行 方 向 一 定 不 是 目 标 函 数 的可行方向一定不是目标函数 的可行方向一定不是目标函数f$的下降方向**,即下列方程组无解
{ ∇ f ( x ∗ ) T d < 0 ∇ g i ( x ∗ ) T d < 0 , i ∈ I \begin{cases} \nabla f(x^*)^T d\lt0 \\ \nabla g_i(x^*)^T d <0, \quad i \in I \end{cases} {∇f(x∗)Td<0∇gi(x∗)Td<0,i∈I
直接理解为,不可能在最优解 x ∗ x^* x∗处,再找到比最优解对应的目标值小且满足约束条件的解。
根据Gordan定理,必存在非零向量 w = ( w 0 , w i , i ∈ I ) ≥ 0 w=(w_0,w_i, i\in I) \geq 0 w=(w0,wi,i∈I)≥0,使得
w 0 ∇ f ( x ∗ ) + ∑ i ∈ I w i ∇ g i ( x ∗ ) = 0 w_0\nabla f(x^*) + \sum_{i\in I}w_i\nabla g_i(x^*)= 0 w0∇f(x∗)+i∈I∑wi∇gi(x∗)=0
引理 Farkas
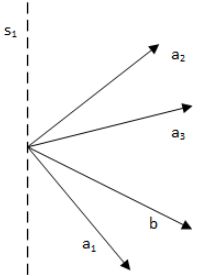
设 a 1 , ⋯ , a m a_1,\cdots,a_m a1,⋯,am和 b b b是n维向量,则存在向量 p p p,满足 a i T p ≥ 0 a_i^Tp\ge 0 aiTp≥0且 b T p ≥ 0 b^Tp\ge 0 bTp≥0的充要条件是,存在非负数 r i r_i ri使得 b = ∑ i = 1 m γ i a i b=\sum\limits_{i=1}^m\gamma_ia_i b=i=1∑mγiai。
简单理解是,向量 p p p与所有 a i a_i ai和 b b b之间的夹角不超过 π \pi π,故向量 b b b与 a i a_i ai位于"同侧",图4左图。
引理 Gordan
设 a 1 , ⋯ , a m a_1,\cdots,a_m a1,⋯,am和 b b b是n维向量,则不存在向量 p p p,使得 a i T p < 0 a_i^Tp\lt0 aiTp<0的充要条件是,存在非负数 r i r_i ri使得 ∑ i = 1 m γ i a i = 0 \sum\limits_{i=1}^m\gamma_ia_i=0 i=1∑mγiai=0。
简单理解是,向量 a 1 , ⋯ , a m a_1, \cdots, a_m a1,⋯,am中,存在夹角超过 π \pi π的两个向量,即 a 1 , ⋯ , a m a1, \cdots, a_m a1,⋯,am位于"不同侧",图4右图。

2.6 Kuhn-Tucker条件(最优解必要条件 - 约束规格)
Fritz John条件中,当 w 0 = 0 w_0=0 w0=0时,梯度组合未包含目标函数信息。著名的K-T条件,增加起作用约束的梯度线性无关的约束规格。若 x ∗ x^* x∗是局部最优解,则存在非负数 w i w_i wi, i ∈ I i\in I i∈I,使得
∇ f ( x ∗ ) + ∑ i ∈ I w i ∇ g i ( x ∗ ) = 0 \nabla f(x^*) + \sum_{i\in I}w_i\nabla g_i(x^*)= 0 ∇f(x∗)+i∈I∑wi∇gi(x∗)=0
证明方法(1)
由存在非零向量 w = ( w 0 , w ^ i , i ∈ I ) ≥ 0 w=(w_0,\hat w_i, i\in I) \geq 0 w=(w0,w^i,i∈I)≥0,使得
w 0 ∇ f ( x ∗ ) + ∑ i ∈ I w ^ i ∇ g i ( x ∗ ) = 0 w_0\nabla f(x^*) + \sum_{i\in I} \hat w_i\nabla g_i(x^*)= 0 w0∇f(x∗)+i∈I∑w^i∇gi(x∗)=0显然 w 0 ≠ 0 w_0\neq0 w0=0,因为 w 0 = 0 w_0=0 w0=0时, { ∇ g i ( x ∗ ) ∣ i ∈ I } \{\nabla g_i(x^*)\,|\,i \in I\} {∇gi(x∗)∣i∈I}线性相关,因此令 w i = w ^ i / w 0 w_i=\hat w_i/w_0 wi=w^i/w0,得
∇ f ( x ∗ ) + ∑ i ∈ I w i ∇ g i ( x ∗ ) = 0 , w i ≥ 0 \nabla f(x^*) + \sum_{i\in I}w_i\nabla g_i(x^*)= 0, \qquad w_i\geq0 ∇f(x∗)+i∈I∑wi∇gi(x∗)=0,wi≥0证明方法(2)
引入辅助函数 L ( x , w ) = f ( x ) + w T g ( x ) L(x, w)=f(x)+w^Tg(x) L(x,w)=f(x)+wTg(x),假设 x ∗ x^* x∗是原问题的最优解,由于 g ( x ) ≤ 0 g(x)\leq0 g(x)≤0, w ≥ 0 w\geq0 w≥0,故
L ( x , w ) = f ( x ) + w T g ( x ) ≥ f ( x ∗ ) L(x, w)=f(x)+w^Tg(x)\geq f(x^*) L(x,w)=f(x)+wTg(x)≥f(x∗)因此, L ( x , w ) L(x, w) L(x,w)在 x ∗ x^* x∗处梯度为 0 0 0,即
∇ f ( x ∗ ) + ∑ i ∈ I w i ∇ g i ( x ∗ ) = 0 , w i ≥ 0 \nabla f(x^*) + \sum_{i\in I}w_i\nabla g_i(x^*)= 0, \qquad w_i\geq0 ∇f(x∗)+i∈I∑wi∇gi(x∗)=0,wi≥0
因此若 g i ( i ∉ I ) g_i(i\notin I) gi(i∈/I)在 x ∗ x^* x∗可微,则 K − T K-T K−T条件的等价形式:
{ ∇ f ( x ∗ ) + ∑ i = 1 m w i ∇ g i ( x ∗ ) = 0 ( 1 ) w i g i ( x ∗ ) = 0 , i = 1 , 2 , ⋯ , m ( 2 ) w i ≥ 0 , i = 1 , 2 , ⋯ , m ( 3 ) \begin{cases} \nabla f(x^*) + \displaystyle\sum\limits_{i=1}^m w_i\nabla g_i(x^*)= 0 &\qquad(1)\\ w_ig_i(x^*)=0, \qquad i=1,2,\cdots,m &\qquad(2)\\ w_i \geq 0,\qquad i=1,2,\cdots,m &\qquad(3) \end{cases} ⎩⎪⎪⎪⎨⎪⎪⎪⎧∇f(x∗)+i=1∑mwi∇gi(x∗)=0wigi(x∗)=0,i=1,2,⋯,mwi≥0,i=1,2,⋯,m(1)(2)(3)
- 当 i ∉ I i\notin I i∈/I时, g i ( x ∗ ) ≠ 0 g_i(x^*)\neq0 gi(x∗)=0,故 w i = 0 w_i=0 wi=0,项 w i ∇ g i ( x ∗ ) w_i\nabla g_i(x^*) wi∇gi(x∗)从 ( 1 ) (1) (1)式中自然消去;
- 当 i ∈ I i\in I i∈I时, g i ( x ∗ ) = 0 g_i(x^*)= 0 gi(x∗)=0,条件 ( 2 ) (2) (2)对 w i w_i wi没有限制,条件 ( 2 ) (2) (2)称为互补松弛条件;
2.7 最优解必要条件
若非线性规划问题中,目标函数 f ( x ) f(x) f(x)和 g ( x ) g(x) g(x)均为凸函数,约束作用集 I = { i ∣ g i ( x ∗ ) = 0 } I = \{i\ |\ g_i(x^*)=0\} I={i ∣ gi(x∗)=0}, f f f和 g i ( i ∈ I ) g_i(i\in I) gi(i∈I)在 x ∗ x^* x∗处可微, g i ( i ∉ I ) g_i(i\notin I) gi(i∈/I)在点 x ∗ x^* x∗处连续,若点 x ∗ x^* x∗处K-T条件成立,则 x ∗ x^* x∗为全局最优解。
证明:显然可行域为凸集, f f f为凸函数,此问题为凸规划。
凸函数 f ( x ) f(x) f(x),满足
f ( x ) ≥ f ( x ∗ ) + ∇ f ( x ∗ ) T ( x − x ∗ ) f(x) \geq f(x^*)+\nabla f(x^*)^T(x- x^*) f(x)≥f(x∗)+∇f(x∗)T(x−x∗)由于 x ∗ x^* x∗处K-T条件成立,故 ∇ f ( x ∗ ) = − ∑ i = 1 m w i ∇ g i ( x ∗ ) \nabla f(x^*) = - \displaystyle\sum\limits_{i=1}^m w_i\nabla g_i(x^*) ∇f(x∗)=−i=1∑mwi∇gi(x∗), w i w_i wi非负,因此
f ( x ) ≥ f ( x ∗ ) − ∑ i ∈ I w i ∇ g i ( x ∗ ) T ( x − x ∗ ) f(x) \geq f(x^*)-\sum\limits_{i\in I}w_i\nabla g_i(x^*)^T(x- x^*) f(x)≥f(x∗)−i∈I∑wi∇gi(x∗)T(x−x∗)同理,由于 g i ( x ) ( i ∈ I ) g_i(x)(i \in I) gi(x)(i∈I)为凸函数,满足
g i ( x ) ≥ g i ( x ∗ ) + ∇ g i ( x ∗ ) T ( x − x ∗ ) g_i(x) \geq g_i(x^*)+\nabla g_i(x^*)^T(x- x^*) gi(x)≥gi(x∗)+∇gi(x∗)T(x−x∗)由于 g i ( x ∗ ) = 0 g_i(x^*)=0 gi(x∗)=0, g i ( x ) ≥ 0 g_i(x)\geq0 gi(x)≥0,故 ∇ g i ( x ∗ ) T ( x − x ∗ ) ≤ 0 \nabla g_i(x^*)^T(x- x^*)\leq0 ∇gi(x∗)T(x−x∗)≤0,因此
f ( x ) ≥ f ( x ∗ ) f(x) \geq f(x^*) f(x)≥f(x∗)
f ( x ∗ ) f(x^*) f(x∗)为最小值,问题得证。
3 对偶问题
考虑非线性规划问题,令 g ( x ) = ( g 1 ( x ) , g 2 ( x ) , ⋯ , g m ( x ) ) T g(x)=(g_1(x), g_2(x), \cdots, g_m(x))^T g(x)=(g1(x),g2(x),⋯,gm(x))T, h ( x ) = ( h 1 ( x ) , h 2 ( x ) , ⋯ , h l ( x ) ) T h(x)=(h_1(x), h_2(x), \cdots, h_l(x))^T h(x)=(h1(x),h2(x),⋯,hl(x))T,则
min x ∈ R n f ( x ) s.t. g ( x ) ≤ 0 h ( x ) = 0 \begin{aligned} \min\limits_{x\in\R^n} &\quad f(x) \\ \text{s.t.} &\quad g(x)\leq 0\\ &\quad h(x) = 0 \end{aligned} x∈Rnmins.t.f(x)g(x)≤0h(x)=0
可行域 S = { x ∣ g ( x ) ≤ 0 ; h ( x ) = 0 } S=\{{x}\ |\ g(x)\leq 0;\ h(x) = 0\} S={x ∣ g(x)≤0; h(x)=0},引入广义拉格朗日函数 L ( x , w , υ ) = f ( x ) + w T g ( x ) + υ T h ( x ) L(x, w, \upsilon)=f(x)+w^T g(x)+\upsilon^T h(x) L(x,w,υ)=f(x)+wTg(x)+υTh(x)。
3.1 原始问题的等价问题
对于上述非线性规划问题,,令
θ P ( x ) = max w , υ L ( x , w , υ ) \theta_P(x) = \max\limits_{w, \upsilon} L(x, w, \upsilon) θP(x)=w,υmaxL(x,w,υ)
(i) x x x违反约束, x ∉ S x \notin S x∈/S,此时 θ P ( x ) → + ∞ \theta_P(x) \to +\infty θP(x)→+∞
当 g i ( x ∗ ) > 0 g_i(x^*)>0 gi(x∗)>0,则可令 w i → + ∞ w_i \to +\infty wi→+∞,当 h i ( x ∗ ) ≠ 0 h_i(x^*)\neq 0 hi(x∗)=0,令 υ i h i ( x ∗ ) → + ∞ \upsilon_ih_i(x ^*) \to +\infty υihi(x∗)→+∞,而将其他 w j w_j wj和 υ j \upsilon_j υj置0,则 θ P ( x ) → + ∞ \theta_P(x) \to +\infty θP(x)→+∞。
(ii) x x x满足约束, x ∈ S x \in S x∈S,此时 θ P ( x ) = f ( x ) \theta_P(x) = f(x) θP(x)=f(x)
当且仅当 x x x位于约束边界时, θ P ( x ) = f ( x ) \theta_P(x) = f(x) θP(x)=f(x)。
综上所述,有
max w , υ L ( x , w , υ ) = { f ( x ) , x ∈ S + ∞ , x ∉ S \max\limits_{w, \upsilon} L(x, w, \upsilon) = \begin{cases} f(x), \quad x \in S\\ +\infty, \quad x \notin S \end{cases} w,υmaxL(x,w,υ)={f(x),x∈S+∞,x∈/S
因此,原始问题的等价问题: min x max w , υ L ( x , w , υ ) \min\limits_{x}\max\limits_{w, \upsilon} L(x, w, \upsilon) xminw,υmaxL(x,w,υ),其中 x ∈ S x \in S x∈S,即拉格朗日极小极大问题,先求最优 w w w和 υ \upsilon υ,再求最优 x x x。
3.2 原始问题的对偶问题
原问题的对偶问题为
max w , υ min x L ( x , w , υ ) s.t. w ≥ 0 \begin{aligned} \max\limits_{w, \upsilon} &\quad\min\limits_{x}L(x, w, \upsilon)\\ \text{s.t.} &\quad w \geq 0\\ \end{aligned} w,υmaxs.t.xminL(x,w,υ)w≥0
对偶问题为拉格朗日极大极小问题,先求最优 x x x,再求最优 w w w和 υ \upsilon υ。
3.3 原始问题与对偶问题关系
当 x ∈ S x \in S x∈S时, g ( x ) ≤ 0 g(x)\leq0 g(x)≤0, h ( x ) = 0 h(x)=0 h(x)=0,且 w ≥ 0 w\geq0 w≥0,因此
min x L ( x , w , υ ) = min x f ( x ) + w T g ( x ) + υ T h ( x ) ≤ f ( x ) \min\limits_{x}L(x, w, \upsilon) =\min_{x}f(x) + w^T g(x)+\upsilon^T h(x) \leq f(x) xminL(x,w,υ)=xminf(x)+wTg(x)+υTh(x)≤f(x)
对上述不等式的左边取上界(max)、右边取下界(min),则不等式仍然成立,即
max w , υ min x L ( x , w , υ ) ≤ min x f ( x ) = min x max w , υ L ( x , w , υ ) \max\limits_{w,\upsilon}\min\limits_{x}L(x, w, \upsilon) \leq \min\limits_{x}f(x)=\min\limits_{x}\max\limits_{w, \upsilon} L(x, w, \upsilon) w,υmaxxminL(x,w,υ)≤xminf(x)=xminw,υmaxL(x,w,υ)
即原问题目标函数的最小值不小于对偶问题目标函数的最大值,弱对偶定理。
原问题的解等价于对偶问题的解成立的条件是什么?(强对偶定理)
(i) 若 f f f和 g g g是凸函数, h h h是仿射函数,若存在 x x x,对所有 i i i满足 g i ( x ) < 0 g_i(x)\lt0 gi(x)<0,则存在 x ∗ , w ∗ , υ ∗ x^*, w^*,\upsilon^* x∗,w∗,υ∗,使 x ∗ x^* x∗是原始问题的解, w ∗ , υ ∗ w^*,\upsilon^* w∗,υ∗是对偶问题的解,且目标值相同。
(ii) 若 f f f和 g g g是凸函数, h h h是仿射函数,且 g i ( x ) ≤ 0 g_i(x)\leq 0 gi(x)≤0,则存在 x ∗ x^* x∗和 w ∗ , υ ∗ w^*,\upsilon^* w∗,υ∗分别是原始问题和对偶问题的解的充分必要条件是 x ∗ , w ∗ , υ ∗ x^*,w^*,\upsilon^* x∗,w∗,υ∗满足KKT条件,即
{ ∇ f ( x ∗ ) + ∑ i = 1 m w i ∇ g i ( x ∗ ) = 0 w i g i ( x ∗ ) = 0 , i = 1 , 2 , ⋯ , m g i ( x ∗ ) ≤ 0 , i = 1 , 2 , ⋯ , m w i ≥ 0 , i = 1 , 2 , ⋯ , m h j ( x ∗ ) = 0 , j = 1 , 2 , ⋯ , l \begin{cases} \nabla f(x^*) + \displaystyle\sum\limits_{i=1}^m w_i\nabla g_i(x^*)= 0 \\ w_ig_i(x^*)=0, \qquad i=1,2,\cdots,m \\ g_i(x^*)\leq 0, \qquad i=1,2,\cdots,m \\ w_i \geq 0,\qquad i=1,2,\cdots,m \\ h_j(x^*)=0,\qquad j=1,2,\cdots,l \end{cases} ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧∇f(x∗)+i=1∑mwi∇gi(x∗)=0wigi(x∗)=0,i=1,2,⋯,mgi(x∗)≤0,i=1,2,⋯,mwi≥0,i=1,2,⋯,mhj(x∗)=0,j=1,2,⋯,l
参考文献:
- 约束优化方法之拉格朗日乘子法与KKT条件:https://www.cnblogs.com/ooon/p/5721119.html
- 约束最优化方法之最优性条件:https://blog.csdn.net/u012430664/article/details/78745729