凸优化学习笔记 2：超平面分离定理

个人博客地址 Glooow，欢迎光临~~~

1. 超平面分离定理

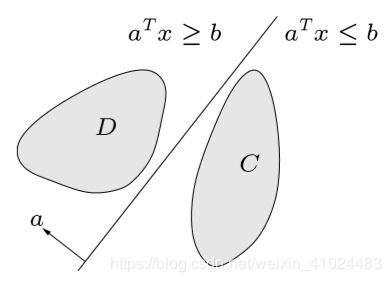
超平面分离定理(Separating hyperplane theorem)：若 $C,D$ 为非空凸集，且 $C\cap D=\varnothing$，则存在 $a\ne 0,b$，使得
$$a^{T}x\le b\text{for}x\in C,a^{T}x\ge b\text{for}x\in D$$
也可以等价表示为 ${\inf }_{x\in D}{a}^{T}x\ge {\sup }_{x\in C}{a}^{T}x$

Lemma 1：$C$ closed，convex，$y\notin C$，那么存在唯一的 $x\in C$，使得 $\Vert y-x\Vert =\inf \{\Vert y-z\Vert |z\in C\}=d(y,C)$

Proof：omit…

Lemma 2：$C$ closed，convex，$y\notin C$，那么存在 $a\ne 0,b$，使得
$$a^{T}y<b,a^{T}x\ge b\forall x\in C$$
Proof：omit…

Remark：上述定理表明存在超平面可以严格分开 $y$ 与 $C$。

Lemma 3：$C$ convex，$y\notin C$，那么存在 $a\ne 0,b$，使得
$$a^{T}y\le b,a^{T}x\ge b\forall x\in C$$
Proof：omit…

超平面分离定理逆定理：若 $C$ 为开集，且存在超平面分离 $C,D$，则 $C\cap D=\varnothing$

2. 支撑超平面定理

支撑超平面：对于集合 $C$ 的边界点 $x_0$，支撑超平面为 $\{x|a^{T}x=a^T{x}_0\}$，其满足 $a\ne 0$ 且 $a^{T}x\le a^T{x}_0,\forall x\in C$

支撑超平面定理：如果 $C$ 为凸集，那么 $C$ 的每个边界点都存在一个支撑超平面