【pytorch】过拟合的应对办法 —— 丢弃法(dropout)
文章目录
- 一、什么是丢弃法,为什么丢弃法可以缓解过拟合?
- 二、丢弃法的手动实现
- 三、丢弃法的pytorch实现
- 参考
- 关于过拟合、欠拟合的解释可以参考我的博文:【pytorch】过拟合和欠拟合详解,并以三阶多项式函数绘图举例 (附pytorch.cat的用法)
- 虽然增大训练数据集可能会减轻过拟合,但是获取额外的训练数据往往代价高昂。本篇博客将介绍应对过拟合问题的常用方法:权重衰减(weight decay)和丢弃法(dropout)。
- 关于权重衰减的讲解参考我的博文:【pytorch】过拟合的应对办法 —— 权重衰减(并以具体实例详细推导、讲解)
一、什么是丢弃法,为什么丢弃法可以缓解过拟合?
由于丢弃法种类有很多,此处以倒置丢弃法(inverted dropout)来讲解。
下式为一个单隐藏层的多层感知机。其中输入个数为4,隐藏单元个数为5,且隐藏单元 h i h_i hi( i = 1 , … , 5 i=1, \ldots, 5 i=1,…,5)的计算表达式为
h i = ϕ ( x 1 w 1 i + x 2 w 2 i + x 3 w 3 i + x 4 w 4 i + b i ) h_i = \phi\left(x_1 w_{1i} + x_2 w_{2i} + x_3 w_{3i} + x_4 w_{4i} + b_i\right) hi=ϕ(x1w1i+x2w2i+x3w3i+x4w4i+bi)
这里 ϕ \phi ϕ是激活函数, x 1 , … , x 4 x_1, \ldots, x_4 x1,…,x4是输入,隐藏单元 i i i的权重参数为 w 1 i , … , w 4 i w_{1i}, \ldots, w_{4i} w1i,…,w4i,偏差参数为 b i b_i bi。当对该隐藏层使用丢弃法时,该层的隐藏单元将有一定概率被丢弃掉。设丢弃概率为 p p p,那么有 p p p的概率 h i h_i hi会被清零,有 1 − p 1-p 1−p的概率 h i h_i hi会除以 1 − p 1-p 1−p做拉伸。丢弃概率是丢弃法的超参数。具体来说,设随机变量 ξ i \xi_i ξi为0和1的概率分别为 p p p和 1 − p 1-p 1−p。使用丢弃法时我们计算新的隐藏单元 h i ′ h_i' hi′
h i ′ = ξ i 1 − p h i h_i' = \frac{\xi_i}{1-p} h_i hi′=1−pξihi
由于 E ( ξ i ) = 1 − p E(\xi_i) = 1-p E(ξi)=1−p,因此
E ( h i ′ ) = E ( ξ i ) 1 − p h i = h i E(h_i') = \frac{E(\xi_i)}{1-p}h_i = h_i E(hi′)=1−pE(ξi)hi=hi
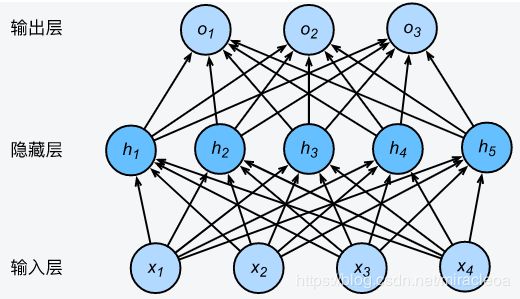
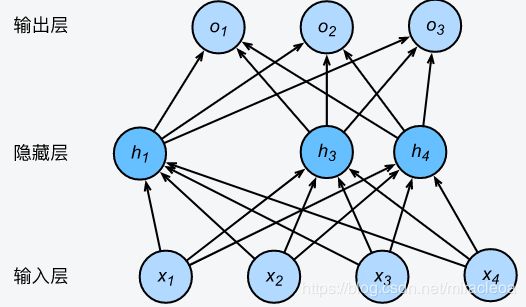
即丢弃法不改变其输入的期望值。让我们对上图多层感知机中的隐藏层使用丢弃法,一种可能的结果如下图所示,其中 h 2 h_2 h2和 h 5 h_5 h5被清零。这时输出值的计算不再依赖 h 2 h_2 h2和 h 5 h_5 h5,在反向传播时,与这两个隐藏单元相关的权重的梯度均为0。由于在训练中隐藏层神经元的丢弃是随机的,即 h 1 , … , h 5 h_1, \ldots, h_5 h1,…,h5都有可能被清零,输出层的计算无法过度依赖 h 1 , … , h 5 h_1, \ldots, h_5 h1,…,h5中的任一个,从而在训练模型时起到正则化的作用,并可以用来应对过拟合。在进行测试模型的步骤时,我们为了拿到更加确定性的结果,一般不使用丢弃法。
def dropout(X, drop_prob):
X = X.float()
assert 0 <= drop_prob <= 1
keep_prob = 1 - drop_prob
# 这种情况下把全部元素都丢弃
if keep_prob == 0:
return torch.zeros_like(X)
mask = (torch.rand(X.shape) < keep_prob).float()
return mask * X / keep_prob
X = torch.arange(16).view(2, 8)
dropout(X, 0)
dropout(X, 0.5)
dropout(X, 1.0)
二、丢弃法的手动实现
- 代码
import torch
import torch.nn as nn
import numpy as np
import torchvision
def evaluate_accuracy(data_iter, net):
acc_sum, n = 0.0, 0
for X, y in data_iter:
if isinstance(net, torch.nn.Module):
net.eval() # 评估模式, 这会关闭dropout
acc_sum += (net(X).argmax(dim=1) == y).float().sum().item()
net.train() # 改回训练模式
else: # 自定义的模型
if ('is_training' in net.__code__.co_varnames): # 如果有is_training这个参数
# 将is_training设置成False
acc_sum += (net(X, is_training=False).argmax(dim=1) == y).float().sum().item()
else:
acc_sum += (net(X).argmax(dim=1) == y).float().sum().item()
n += y.shape[0]
return acc_sum / n
def load_data_fashion_mnist(batch_size, resize=None, root='./data'):
"""Download the fashion mnist dataset and then load into memory."""
trans = []
if resize:
trans.append(torchvision.transforms.Resize(size=resize))
trans.append(torchvision.transforms.ToTensor())
transform = torchvision.transforms.Compose(trans)
mnist_train = torchvision.datasets.FashionMNIST(root=root, train=True, download=True, transform=transform)
mnist_test = torchvision.datasets.FashionMNIST(root=root, train=False, download=True, transform=transform)
num_workers = 0 # 0表示不用额外的进程来加速读取数据
train_iter = torch.utils.data.DataLoader(mnist_train, batch_size=batch_size, shuffle=True, num_workers=num_workers)
test_iter = torch.utils.data.DataLoader(mnist_test, batch_size=batch_size, shuffle=False, num_workers=num_workers)
return train_iter, test_iter
def dropout(X, drop_prob):
X = X.float()
assert 0 <= drop_prob <= 1
keep_prob = 1 - drop_prob
# 这种情况下把全部元素都丢弃
if keep_prob == 0:
return torch.zeros_like(X)
mask = (torch.rand(X.shape) < keep_prob).float()
return mask * X / keep_prob
def net(X, is_training=True):
X = X.view(-1, num_inputs)
H1 = (torch.matmul(X, W1) + b1).relu()
if is_training: # 只在训练模型时使用丢弃法
H1 = dropout(H1, drop_prob1) # 在第一层全连接后添加丢弃层
H2 = (torch.matmul(H1, W2) + b2).relu()
if is_training:
H2 = dropout(H2, drop_prob2) # 在第二层全连接后添加丢弃层
return torch.matmul(H2, W3) + b3
def sgd(params, lr, batch_size):
# 为了和原书保持一致,这里除以了batch_size,但是应该是不用除的,因为一般用PyTorch计算loss时就默认已经
# 沿batch维求了平均了。
for param in params:
param.data -= lr * param.grad / batch_size # 注意这里更改param时用的param.data
def train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size,
params=None, lr=None, optimizer=None):
for epoch in range(num_epochs):
train_l_sum, train_acc_sum, n = 0.0, 0.0, 0
for X, y in train_iter:
y_hat = net(X)
l = loss(y_hat, y).sum()
# 梯度清零
if optimizer is not None:
optimizer.zero_grad()
elif params is not None and params[0].grad is not None:
for param in params:
param.grad.data.zero_()
l.backward()
if optimizer is None:
sgd(params, lr, batch_size)
else:
optimizer.step() # “softmax回归的简洁实现”一节将用到
train_l_sum += l.item()
train_acc_sum += (y_hat.argmax(dim=1) == y).sum().item()
n += y.shape[0]
test_acc = evaluate_accuracy(test_iter, net)
print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f'
% (epoch + 1, train_l_sum / n, train_acc_sum / n, test_acc))
if __name__ == '__main__':
num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10, 256, 256
W1 = torch.tensor(np.random.normal(0, 0.01, size=(num_inputs, num_hiddens1)), dtype=torch.float, requires_grad=True)
b1 = torch.zeros(num_hiddens1, requires_grad=True)
W2 = torch.tensor(np.random.normal(0, 0.01, size=(num_hiddens1, num_hiddens2)), dtype=torch.float,
requires_grad=True)
b2 = torch.zeros(num_hiddens2, requires_grad=True)
W3 = torch.tensor(np.random.normal(0, 0.01, size=(num_hiddens2, num_outputs)), dtype=torch.float,
requires_grad=True)
b3 = torch.zeros(num_outputs, requires_grad=True)
params = [W1, b1, W2, b2, W3, b3]
drop_prob1, drop_prob2 = 0.2, 0.5
num_epochs, lr, batch_size = 5, 100.0, 256
loss = torch.nn.CrossEntropyLoss()
train_iter, test_iter = load_data_fashion_mnist(batch_size)
train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size, params, lr)
- 结果
epoch 1, loss 0.0047, train acc 0.538, test acc 0.723
epoch 2, loss 0.0023, train acc 0.779, test acc 0.779
epoch 3, loss 0.0020, train acc 0.818, test acc 0.807
epoch 4, loss 0.0018, train acc 0.838, test acc 0.832
epoch 5, loss 0.0016, train acc 0.848, test acc 0.843
三、丢弃法的pytorch实现
- 代码
import torch
import torch.nn as nn
import numpy as np
import torchvision
from d2lzh_pytorch import utils as d2l
def evaluate_accuracy(data_iter, net):
acc_sum, n = 0.0, 0
for X, y in data_iter:
# isinstance()函数来判断一个对象是否是一个已知的类型,类似type()。
# isinstance()与type()区别:
# type()不会认为子类是一种父类类型,不考虑继承关系。
# isinstance()会认为子类是一种父类类型,考虑继承关系。如果要判断两个类型是否相同推荐使用isinstance()。
if isinstance(net, torch.nn.Module):
net.eval() # 评估模式, 这会关闭dropout
acc_sum += (net(X).argmax(dim=1) == y).float().sum().item()
net.train() # 改回训练模式
else: # 自定义的模型
if ('is_training' in net.__code__.co_varnames): # 如果有is_training这个参数
# 将is_training设置成False
acc_sum += (net(X, is_training=False).argmax(dim=1) == y).float().sum().item()
else:
acc_sum += (net(X).argmax(dim=1) == y).float().sum().item()
n += y.shape[0]
return acc_sum / n
def load_data_fashion_mnist(batch_size, resize=None, root='./data'):
"""Download the fashion mnist dataset and then load into memory."""
trans = []
if resize:
trans.append(torchvision.transforms.Resize(size=resize))
trans.append(torchvision.transforms.ToTensor())
transform = torchvision.transforms.Compose(trans)
mnist_train = torchvision.datasets.FashionMNIST(root=root, train=True, download=True, transform=transform)
mnist_test = torchvision.datasets.FashionMNIST(root=root, train=False, download=True, transform=transform)
num_workers = 0 # 0表示不用额外的进程来加速读取数据
train_iter = torch.utils.data.DataLoader(mnist_train, batch_size=batch_size, shuffle=True, num_workers=num_workers)
test_iter = torch.utils.data.DataLoader(mnist_test, batch_size=batch_size, shuffle=False, num_workers=num_workers)
return train_iter, test_iter
# Flatten层用来将输入“压平”,即把多维的输入一维化,常用在从卷积层到全连接层的过渡。Flatten不影响batch的大小。
class FlattenLayer(torch.nn.Module):
def __init__(self):
super(FlattenLayer, self).__init__()
def forward(self, x): # x shape: (batch, *, *, ...)
return x.view(x.shape[0], -1)
def train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size,
params=None, lr=None, optimizer=None):
for epoch in range(num_epochs):
train_l_sum, train_acc_sum, n = 0.0, 0.0, 0
for X, y in train_iter:
y_hat = net(X)
l = loss(y_hat, y).sum()
# 梯度清零
if optimizer is not None:
optimizer.zero_grad()
elif params is not None and params[0].grad is not None:
for param in params:
param.grad.data.zero_()
l.backward()
# 所有的optimizer都实现了step()方法,这个方法会更新所有的参数。
optimizer.step() # “softmax回归的简洁实现”一节将用到
train_l_sum += l.item()
train_acc_sum += (y_hat.argmax(dim=1) == y).sum().item()
n += y.shape[0]
test_acc = evaluate_accuracy(test_iter, net)
print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f'
% (epoch + 1, train_l_sum / n, train_acc_sum / n, test_acc))
if __name__ == '__main__':
num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10, 256, 256
drop_prob1, drop_prob2 = 0.2, 0.5
num_epochs, batch_size = 5, 256
loss = torch.nn.CrossEntropyLoss()
net = nn.Sequential(
FlattenLayer(),
nn.Linear(num_inputs, num_hiddens1),
nn.ReLU(),
nn.Dropout(drop_prob1),
nn.Linear(num_hiddens1, num_hiddens2),
nn.ReLU(),
nn.Dropout(drop_prob2),
nn.Linear(num_hiddens2, num_outputs)
)
for param in net.parameters():
nn.init.normal_(param, mean=0, std=0.01)
optimizer = torch.optim.SGD(net.parameters(), lr=0.5)
train_iter, test_iter = load_data_fashion_mnist(batch_size)
train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size, None, None, optimizer)
- 结果
epoch 1, loss 0.0044, train acc 0.561, test acc 0.771
epoch 2, loss 0.0023, train acc 0.787, test acc 0.757
epoch 3, loss 0.0019, train acc 0.825, test acc 0.829
epoch 4, loss 0.0017, train acc 0.841, test acc 0.788
epoch 5, loss 0.0016, train acc 0.846, test acc 0.814
参考
【pytorch】过拟合和欠拟合详解,并以三阶多项式函数绘图举例 (附pytorch.cat的用法)
【pytorch】过拟合的应对办法 —— 权重衰减(并以具体实例详细推导、讲解)
动手学深度学习