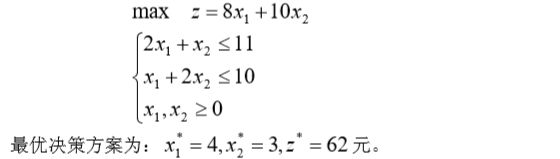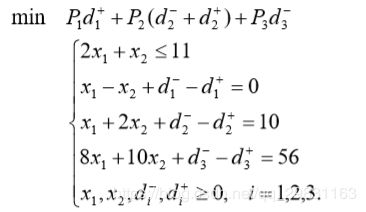目标规划模型:求解思路、序贯式算法
目录
1.线性规划的局限性
2.实际决策中,衡量方案优劣考虑多个目标
3.目标规划(Goal Programming)
4.求解思路 (1)加权系数法 (2)优先等级法 (3)有效解法
2 目标规划的数学模型
1. 正、负偏差变量 2. 绝对(刚性)约束和目标约束
3. 优先因子(优先等级)与权系数 4. 目标规划的目标函数
5.目标规划的一般数学模型
3 求解目标规划的序贯式算法
4 多标规划的 Matlab 解法 习题
1.线性规划的局限性
只能解决一组线性约束条件下,某一目标只能是一个目标的最大或最小值的问题。
2.实际决策中,衡量方案优劣考虑多个目标
这些目标中,有主要的,也有次要的;有最大值的,也有最小值的;有定量的, 也有定性的;有相互补充的,也有相互对立的,LP 则无能为力。
3.目标规划(Goal Programming)
美国经济学家查恩斯(A. Charnes)和库柏(W. W. Cooper)在 1961 年出版的《管理模型及线性规划的工业应用》一书中,首先提出的。
4.求解思路
(1)加权系数法
为每一目标赋一个权系数,把多目标模型转化成单一目标的模型。但困难是要确 定合理的权系数,以反映不同目标之间的重要程度。
(2)优先等级法
将各目标按其重要程度不同的优先等级,转化为单目标模型。
(3)有效解法
寻求能够照顾到各个目标,并使决策者感到满意的解。由决策者来确定选取哪一个 解,即得到一个满意解。但有效解的数目太多而难以将其一一求出。
2 目标规划的数学模型
为了具体说明目标规划与线性规划在处理问题的方法上的区别,先通过例子来介绍 目标规划的有关概念及数学模型。
例1 某工厂生产 I,II 两种产品,已知有关数据见下表 ,试求获利最大的生产方案。
解 这是一个单目标的规划问题,用线性规划模型表述为:
但实际上工厂在作决策方案时,要考虑市场等一系列其它条件。如
(i)根据市场信息,产品 I 的销售量有下降的趋势,故考虑产品 I 的产量不大于 产品 II。
(ii)超过计划供应的原材料,需要高价采购,这就使成本增加。
(iii)应尽可能充分利用设备,但不希望加班。
(iv)应尽可能达到并超过计划利润指标 56 元。
这样在考虑产品决策时,便为多目标决策问题。目标规划方法是解决这类决策问题 的方法之一。下面引入与建立目标规划数学模型有关的概念。
1. 正、负偏差变量
2. 绝对(刚性)约束和目标约束
3. 优先因子(优先等级)与权系数
4. 目标规划的目标函数
对每一个具体目标规划问题,可根据决策者的要求和赋于各目标的优先因子来构造目标 函数,以下用例子说明。
例 2 : 例 1 的决策者在原材料供应受严格限制的基础上考虑:首先是产品 II 的产 量不低于产品 I 的产量;其次是充分利用设备有效台时,不加班;再次是利润额不小于 56 元。求决策方案。 解 按决策者所要求的,分别赋于这三个目标![]() 优先因子。这问题的数学模型是
优先因子。这问题的数学模型是
5.目标规划的一般数学模型
建立目标规划的数学模型时,需要确定目标值、优先等级、权系数等,它都具有一 定的主观性和模糊性,可以用专家评定法给以量化。
3 求解目标规划的序贯式算法
序贯式算法是求解目标规划的一种早期算法,其核心是根据优先级的先后次序, 将目标规划问题分解成一系列的单目标规划问题,然后再依次求解。
注 此时最优解的概念与线性规划最优解的概念已有所不同,但为方便起见,仍 称为最优解。
例 3 某企业生产甲、乙两种产品,需要用到 A ,B ,C 三种设备,关于产品的赢利 与使用设备的工时及限制如下表所示。问该企业应如何安排生产,才能达到下列目标:
(1)力求使利润指标不低于 1500 元;
(2)考虑到市场需求,甲、乙两种产品的产量比应尽量保持 1:2;
(3)设备 A为贵重设备,严格禁止超时使用;
(4)设备 C 可以适当加班,但要控制;设备B 既要求充分利用,又尽可能不加班。 在重要性上,设备B 是设备C 的 3 倍。
建立相应的目标规划模型并求解。
解 设备 A是刚性约束,其余是柔性约束。首先,最重要的指标是企业的利润, 因此,将它的优先级列为第一级;其次,甲、乙两种产品的产量保持 1:2 的比例,列为 第二级;再次,设备 B C, 的工作时间要有所控制,列为第三级。在第三级中,设备B 的 重要性是设备C 的三倍,因此,它们的权重不一样,设备B 前的系数是设备C 前系数 的 3 倍。由此得到相应的目标规划模型。
序贯算法中每个单目标问题都是一个线性规划问题,可以使用 LINGO 软件进行求 解。 求第一级目标。LINGO 程序如下:
model:
sets:
variable/1..2/:x;
S_Con_Num/1..4/:g,dplus,dminus;
S_con(S_Con_Num,Variable):c;
endsets
data:
g=1500 0 16 15;
c=200 300 2 -1 4 0 0 5;
enddata
min=dminus(1);
2*x(1)+2*x(2)<12;
@for(S_Con_Num(i):@sum(Variable(j):c(i,j)*x(j))+dminus(i)-dplus(i )=g(i));
end求得 dminus(1)=0,即目标函数的最优值为 0,第一级偏差为 0。
求第二级目标,LINGO 程序如下:
model:
sets:
variable/1..2/:x;
S_Con_Num/1..4/:g,dplus,dminus;
S_con(S_Con_Num,Variable):c;
endsets
data:
g=1500 0 16 15;
c=200 300 2 -1 4 0 0 5;
enddata
min=dplus(2)+dminus(2); !二级目标函数;
2*x(1)+2*x(2)<12;
@for(S_Con_Num(i):@sum(Variable(j):c(i,j)*x(j))+dminus(i)-dplus(i )=g(i));
dminus(1)=0;!一级目标约束;
@for(variable:@gin(x));
end 求得目标函数的最优值为 0,即第二级的偏差仍为 0。 求第三级目标,LINGO 程序如下:
model:
sets:
variable/1..2/:x;
S_Con_Num/1..4/:g,dplus,dminus;
S_con(S_Con_Num,Variable):c;
endsets
data:
g=1500 0 16 15;
c=200 300 2 -1 4 0 0 5;
enddata
min=3*dplus(3)+3*dminus(3)+dplus(4); !三级目标函数;
2*x(1)+2*x(2)<12;
@for(S_Con_Num(i):@sum(Variable(j):c(i,j)*x(j))+dminus(i)-dplus(i )=g(i));
dminus(1)=0;!一级目标约束;
dplus(2)+dminus(2)=0;!二级目标约束;
end目标函数的最优值为29,即第三级偏差为29。
分析计算结果,![]() ,因此,目标规划的最优解为
,因此,目标规划的最优解为 ![]() , 最优利润为1600。
, 最优利润为1600。
上述过程虽然给出了目标规划问题的最优解,但需要连续编几个程序,这样在使 用时不方便,下面用 LINGO 软件,编写一个通用的程序,在程序中用到数据段未知数 据的编程方法。
例 4(续例 3) 按照序贯式算法,编写求解例 3 的通用 LINGO 程序。
model:
sets:
level/1..3/:p,z,goal;
variable/1..2/:x;
h_con_num/1..1/:b;
s_con_num/1..4/:g,dplus,dminus;
h_con(h_con_num,variable):a;
s_con(s_con_num,variable):c;
obj(level,s_con_num)/1 1,2 2,3 3,3 4/:wplus,wminus;
endsets
data:
ctr=?;
goal=? ? 0;
b=12;
g=1500 0 16 15;
a=2 2;
c=200 300 2 -1 4 0 0 5;
wplus=0 1 3 1;
wminus=1 1 3 0;
enddata
min=@sum(level:p*z);
p(ctr)=1;
@for(level(i)|i#ne#ctr:p(i)=0);
@for(level(i):z(i)=@sum(obj(i,j):wplus(i,j)*dplus(j)+wminus(i,j)* dminus(j))); @for(h_con_num(i):@sum(variable(j):a(i,j)*x(j))4 多标规划的 Matlab 解法
多目标规划可以归结为
[x,fval]= fgoalattain('fun',x0,goal,weight)
[x,fval]= fgoalattain('fun',x0,goal,weight,A,b)
[x,fval]= fgoalattain('fun',x0,goal,weight,A,b,Aeq,beq)
[x,fval]= fgoalattain('fun',x0,goal,weight,A,b,Aeq,beq,lb,ub,nonlcon) 要完整掌握其用法,请用 help fgoalattain 或 type fgoalattain 查询相关的帮助。
例 5 求解多目标线性规划问题
解 (i)编写 M 函数 Fun.m:
function F=Fun(x);
F(1)=-100*x(1)-90*x(2)-80*x(2)-70*x(4);
F(2)=3*x(2)+2*x(4); (ii)编写 M 文件
a=[-1 -1 0 0
0 0 -1 -1
3 0 2 0
0 3 0 2];
b=[-30 -30 120 48]';
c1=[-100 -90 -80 -70];
c2=[0 3 0 2];
[x1,g1]=linprog(c1,a,b,[],[],zeros(4,1)) %求第一个目标函数的目标值
[x2,g2]=linprog(c2,a,b,[],[],zeros(4,1)) %求第二个目标函数的目标值
g3=[g1;g2] %目标goal的值
[x,fval]=fgoalattain('Fun',rand(4,1),g3,abs(g3),a,b,[],[],zeros(4 ,1))
%这里权重weight=目标goal的绝对值 就可求得问题的解。
习题
下一篇:目标规划模型的实例分析