凸优化学习-(六)常见集合
凸优化学习
依然是一些集合。
学习笔记
一、多面体 polyhedron
形如:
P = { ∣ a j T ≤ b j , j = 1 , ⋯ , m c j T x = d j , j = 1 , ⋯ , q } P=\lbrace \mid{ \begin{matrix} a_j ^T\le b_j,j=1,\cdots,m\\ c_j^Tx=d_j,j=1,\cdots,q \end{matrix} }\rbrace P={∣ajT≤bj,j=1,⋯,mcjTx=dj,j=1,⋯,q}
多面体是半空间和超平面的交集,它是凸集。
可以这么理解,多个超平面构成多面体的边,多个超空间构成多面体的内部。
二、单纯形 simplex
定义:
在 R n R^n Rn空间中选择 v 0 , ⋯ , v k v_0,\cdots,v_k v0,⋯,vk共 k + 1 k+1 k+1个点, v 1 − v 0 , ⋯ , v k − v 0 v_1-v_0,\cdots,v_k-v_0 v1−v0,⋯,vk−v0线性无关,则与上述点相关的单纯形为:
C = C o n v { v 0 , ⋯ , v k } = { θ 0 v 0 + ⋯ + θ q v q θ ≥ 0 1 T θ = 1 ∀ v q ∈ [ v 0 , ⋯ , v k ] } \begin{aligned} C &=Conv\lbrace v_0,\cdots,v_k \rbrace\\ &=\lbrace \begin{matrix} \theta_0v_0+\cdots+\theta_qv_q \\ \theta \ge0\ \ 1^T\theta=1 \ \ \forall v_q\in[v_0,\cdots,v_k] \end{matrix} \rbrace \\ \end{aligned} C=Conv{v0,⋯,vk}={θ0v0+⋯+θqvqθ≥0 1Tθ=1 ∀vq∈[v0,⋯,vk]}
举例说明:
考虑一个 R 2 R^2 R2空间:
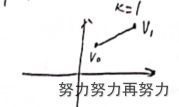
图一中 v 0 , v 1 v_0,v_1 v0,v1的单纯形为线段。
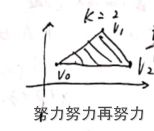
图二中 v 0 , v 1 , v 2 v_0,v_1,v_2 v0,v1,v2三点的单纯形为一个三角形。

图三中的三个向量就不是线性无关的了,事实上,二维空间里面是找不到三个线性无关的向量的。
对于单纯形,有下述结论:
- n n n维空间里, k > n k>n k>n时,这 k k k个点是不存在单纯形的。
- 单纯形一定是多面体。
下面对结论2进行证明。
**命题:**单纯形一定是多面体(Simplex是Polyhedron的一种)
证明: x ∈ C ∈ R n , C x\in C \in R^n,C x∈C∈Rn,C为Simplex ⇔ x = { θ 0 v 0 + ⋯ + θ k v k θ ≥ 0 1 T θ = 1 } \Leftrightarrow x=\lbrace \begin{matrix} \theta_0v_0+\cdots+\theta_kv_k \\ \theta \ge0\ \ 1^T\theta=1 \end{matrix} \rbrace ⇔x={θ0v0+⋯+θkvkθ≥0 1Tθ=1} , v 1 − v 0 , ⋯ , v k − v 0 ,v_1-v_0,\cdots,v_k-v_0 ,v1−v0,⋯,vk−v0线性无关
在此作两个定义:
1. [ θ 1 , ⋯ , θ k ] T = y y ≥ 0 , 1 T y ≤ 1 \begin{bmatrix} \theta_1,\cdots,\theta_k \end{bmatrix}^T=y\ \ \ \ y\ge0,\ 1^Ty\le1 [θ1,⋯,θk]T=y y≥0, 1Ty≤1(这里去除了 θ 0 \theta_0 θ0),
2. [ v 1 − v 0 , ⋯ , v k − v 0 ] = B ∈ R n × k \begin{bmatrix} v_1-v_0,\cdots,v_k-v_0 \end{bmatrix}=\textbf{B}\in \textbf{R}^{n×k} [v1−v0,⋯,vk−v0]=B∈Rn×k
继续证明:
x ∈ C ⇔ x = θ 0 v 0 + ⋯ + θ k v k = v 0 + θ 1 ( v 1 − v 0 ) + ⋯ + θ k ( v k − v 0 ) = v 0 + B y ⇔ A x = A v 0 + AB y ⇔ [ A 1 A 2 ] x = [ A 1 A 2 ] v 0 + [ A1B A2B ] y ⇔ { A 1 x = A 1 v 0 + y A 2 x = A 2 v 0 ⇔ { A 1 x ≥ A 1 v 0 1 T A 1 x ≤ 1 + 1 T A 1 v 0 A 2 x = A 2 v 0 \begin{aligned} x\in C \Leftrightarrow& &x&=\theta_0 v_0+\cdots+\theta_kv_k\\ && &=v_0+\theta_1(v_1-v_0)+\cdots+\theta_k(v_k-v_0)\\ && &=v_0+\textbf By\\ \Leftrightarrow& & \textbf Ax&=\textbf Av_0+\textbf{AB}y \\ \Leftrightarrow & &\begin{bmatrix} \textbf A_1 \\ \textbf A_2 \end{bmatrix}x&=\begin{bmatrix} \textbf A_1 \\ \textbf A_2 \end{bmatrix}v_0+ \begin{bmatrix} \textbf{A1}\textbf B \\ \textbf{A2}\textbf B \end{bmatrix}y \\ \Leftrightarrow & & \left\{ \begin{aligned} \textbf A_1x &=\textbf A_1 v_0+y\\ \textbf A_2x &=\textbf A_2 v_0 \end{aligned} \right.\\ \Leftrightarrow & & \left\{ \begin{aligned} \textbf A_1x &\ge\textbf A_1 v_0\\ 1^T\textbf A_1x &\le1+1^T\textbf A_1v_0\\ \textbf A_2x &=\textbf A_2 v_0 \end{aligned} \right. \end{aligned} x∈C⇔⇔⇔⇔⇔xAx[A1A2]x{A1xA2x=A1v0+y=A2v0⎩⎪⎨⎪⎧A1x1TA1xA2x≥A1v0≤1+1TA1v0=A2v0=θ0v0+⋯+θkvk=v0+θ1(v1−v0)+⋯+θk(vk−v0)=v0+By=Av0+ABy=[A1A2]v0+[A1BA2B]y
三、矩阵集合
1.对称矩阵集合
形如:
S n = { X ∈ R n × n ∣ X = X T } \textbf S^n=\lbrace \textbf X\in \textbf R^{n×n}\mid\textbf X= \textbf X^T \rbrace Sn={X∈Rn×n∣X=XT}
是凸锥。
2.对称半正定矩阵集合
形如:
S + n = { X ∈ R n × n ∣ X = X T X ⪰ 0 } \textbf S^n_+=\lbrace \textbf X\in \textbf R^{n×n}\mid\textbf X= \textbf X^T \ \ \textbf X \succeq0\rbrace S+n={X∈Rn×n∣X=XT X⪰0}
是凸锥。
3.对称正定矩阵集合
形如:
S + + n = { X ∈ R n × n ∣ X = X T X ≻ 0 } \textbf S^n_{++}=\lbrace \textbf X\in \textbf R^{n×n}\mid\textbf X= \textbf X^T \ \ \textbf X \succ0\rbrace S++n={X∈Rn×n∣X=XT X≻0}
是凸集。
个人思考
从这里能够明显的感受到,一是定义在证明中的作用,二是矩阵的作用越来越大。很多结论都是由定义直接推理出来的,但是一些在矩阵空间内的集合,靠想象是没办法推导的,只能多利用矩阵工具。

