gradient checking(梯度检验)
Gradient Checking(梯度检验)
我们有时候实现完backward propagation,我们不知道自己实现的backward propagation到底是不是完全正确的(这篇博客只面向自己手撸的网络,直接搬砖的不需要考虑这个问题…),因此,通常要用梯度检验来检查自己实现的bp是否正确。其实所谓梯度检验,就是自己实现下导数的定义,去求w和b的导数(梯度),然后去和bp求到的梯度比较,如果差值在很小的范围内,则可以认为我们实现的bp没问题。
先来回顾下,导数的定义:
具体应用到神经网络的梯度检验中,因为我们没法做到 Δ x → 0 \Delta x \rightarrow 0 Δx→0,只能取一个比较小的数,所以为了结果更精确,我们可以把上面的公式稍微变下形:
通常设置 ε = e − 7 \varepsilon = e^{-7} ε=e−7即可。
具体到神经网络中,我们做梯度检验的步骤通常为:
- 把 W [ 1 ] , b [ 1 ] , . . . . . . , W [ L ] , b [ L ] W^{[1]},b^{[1]},......,W^{[L]},b^{[L]} W[1],b[1],......,W[L],b[L] 转化成向量 θ \theta θ。
- 同样把 d W [ 1 ] , d b [ 1 ] , . . . . . . , d W [ L ] , d b [ L ] dW^{[1]},db^{[1]},......,dW^{[L]},db^{[L]} dW[1],db[1],......,dW[L],db[L] 转化成向量 d θ d\theta dθ。
- 接下来是实现导数定义:
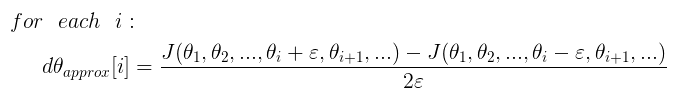
- 接下来我们比较 d θ a p p r o x d\theta_{approx} dθapprox 与 d θ d\theta dθ 是否大致相等,主要是计算两个向量之间的欧式距离:

通常设置阈值 t h r e s h o l d = e − 7 threshold = e^{-7} threshold=e−7。 如果difference小于阈值,则认为实现的bp没问题。
关于上面的步骤,我们来看看代码实现,
1.把 W [ 1 ] , b [ 1 ] , . . . . . . , W [ L ] , b [ L ] W^{[1]},b^{[1]},......,W^{[L]},b^{[L]} W[1],b[1],......,W[L],b[L] 转化成向量 θ \theta θ。
#convert parameter into vector
def dictionary_to_vector(parameters):
"""
Roll all our parameters dictionary into a single vector satisfying our specific required shape.
"""
count = 0
for key in parameters:
# flatten parameter
new_vector = np.reshape(parameters[key], (-1, 1))#convert matrix into vector
if count == 0:#刚开始时新建一个向量
theta = new_vector
else:
theta = np.concatenate((theta, new_vector), axis=0)#和已有的向量合并成新向量
count = count + 1
return theta
2.把 d W [ 1 ] , d b [ 1 ] , . . . . . . , d W [ L ] , d b [ L ] dW^{[1]},db^{[1]},......,dW^{[L]},db^{[L]} dW[1],db[1],......,dW[L],db[L] 转化成向量 d θ d\theta dθ。
注:这个地方一定要注意bp求得的gradients字典的存储顺序是{dWL,dbL,…dW2,db2,dW1,db1},因为后面要求欧式距离,所以一定要把顺序转化为[dW1,db1,…dWL,dbL]。在这个地方踩过坑,花了很长时间才找出bug。
#convert gradients into vector
def gradients_to_vector(gradients):
"""
Roll all our parameters dictionary into a single vector satisfying our specific required shape.
"""
# 因为gradient的存储顺序是{dWL,dbL,....dW2,db2,dW1,db1},
#为了统一采用[dW1,db1,...dWL,dbL]方面后面求欧式距离(对应元素)
L = len(gradients) // 2
keys = []
for l in range(L):
keys.append("dW" + str(l + 1))
keys.append("db" + str(l + 1))
count = 0
for key in keys:
# flatten parameter
new_vector = np.reshape(gradients[key], (-1, 1))#convert matrix into vector
if count == 0:#刚开始时新建一个向量
theta = new_vector
else:
theta = np.concatenate((theta, new_vector), axis=0)#和已有的向量合并成新向量
count = count + 1
return theta
第三步、第四步的代码如下:
def gradient_check(parameters, gradients, X, Y, layer_dims, epsilon=1e-7):
"""
Checks if backward_propagation_n computes correctly the gradient of the cost output by forward_propagation_n
Arguments:
parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":
grad -- output of backward_propagation_n, contains gradients of the cost with respect to the parameters.
x -- input datapoint, of shape (input size, 1)
y -- true "label"
epsilon -- tiny shift to the input to compute approximated gradient with formula(1)
layer_dims -- the layer dimension of nn
Returns:
difference -- difference (2) between the approximated gradient and the backward propagation gradient
"""
parameters_vector = dictionary_to_vector(parameters) # parameters_values
grad = gradients_to_vector(gradients)
num_parameters = parameters_vector.shape[0]
J_plus = np.zeros((num_parameters, 1))
J_minus = np.zeros((num_parameters, 1))
gradapprox = np.zeros((num_parameters, 1))
# Compute gradapprox
for i in range(num_parameters):
thetaplus = np.copy(parameters_vector)
thetaplus[i] = thetaplus[i] + epsilon
AL, _ = forward_propagation(X, vector_to_dictionary(thetaplus,layer_dims))
J_plus[i] = compute_cost(AL,Y)
thetaminus = np.copy(parameters_vector)
thetaminus[i] = thetaminus[i] - epsilon
AL, _ = forward_propagation(X, vector_to_dictionary(thetaminus, layer_dims))
J_minus[i] = compute_cost(AL,Y)
gradapprox[i] = (J_plus[i] - J_minus[i]) / (2 * epsilon)
numerator = np.linalg.norm(grad - gradapprox)
denominator = np.linalg.norm(grad) + np.linalg.norm(gradapprox)
difference = numerator / denominator
if difference > 2e-7:
print(
"\033[93m" + "There is a mistake in the backward propagation! difference = " + str(difference) + "\033[0m")
else:
print(
"\033[92m" + "Your backward propagation works perfectly fine! difference = " + str(difference) + "\033[0m")
return difference
这里在每一次计算bp时,还要把向量转化成矩阵,具体实现如下:
#convert vector into dictionary
def vector_to_dictionary(theta, layer_dims):
"""
Unroll all our parameters dictionary from a single vector satisfying our specific required shape.
"""
parameters = {}
L = len(layer_dims) # the number of layers in the network
start = 0
end = 0
for l in range(1, L):
end += layer_dims[l]*layer_dims[l-1]
parameters["W" + str(l)] = theta[start:end].reshape((layer_dims[l],layer_dims[l-1]))
start = end
end += layer_dims[l]*1
parameters["b" + str(l)] = theta[start:end].reshape((layer_dims[l],1))
start = end
return parameters
还是拿sklearn中自带的breast_cancer数据集,来测试下,自己实现的bp到底对不对,顺便也是测下我们的gradient checking的代码对不对,测试结果如下: >Your backward propagation works perfectly fine! difference = 5.649104934345307e-11
可以看到我们实现的bp求到的梯度和用导数定义实现的梯度之间的差距是 e − 11 e^{-11} e−11这个数量级,所以我们实现的bp正确无误。
完整的代码已放到github上:gradient_checking.py
cs231n中也有讲解关于gradient cheking的资料,不过它的 r e l a t i v e e r r o r relative \ error relative error 定义和ng讲的有些细微的差别,不过不是什么大问题,只是定义不一样而已,只要改变相应的阈值即可。具体见:CS231n Convolutional Neural Networks for Visual Recognition
参考资料 - ng Coursera 《Improving Deep Neural Networks Hyperparameter tuning, Regularization and Optimization》课