机器学习-李宏毅(2019) Machine Learning 01笔记
文章目录
- 回归的定义和应用举例
- 回归定义
- 应用举例
- 模型步骤——机器学习三板斧
- Step1: 模型假设 - 线性模型
- 一元线性模型(单个特征)
- Step2:模型评估 - 损失函数
- 收集和查看训练数据
- 如何判断众多模型的好坏
- Step 3:最佳模型 - 梯度下降
- 如何筛选最优的模型(参数w,b)
- 只有一个参数
- 有两个参数
- 梯度下降推演最优模型的过程
- 梯度下降算法在现实世界中面临的挑战
- 当前最优问题
- w和b偏微分的计算方法
- 如何验证训练好的模型的好坏
- 更强大复杂的模型:1元N次线性模型
- 过拟合问题出现
- 步骤优化
- Step1优化:2个input的四个线性模型是合并到一个线性模型中
- Step2优化:如果希望模型更强大表现更好(更多参数,更多input)
- Step3优化:加入正则化
- 首先看$\lambda$的变化对training data上的error部分的影响
- 再看$\lambda$的变化对testing data上的error部分的影响
- 总结
回归的定义和应用举例
回归定义
regression就是找到一个函数function,通过输入特征x,输出一个数值scalar。
应用举例
- 股市预测
输入:过去10年股票的变动的资料
输出:预测明天股市的指数 - 自动驾驶
输入:无人车上各个sensor的数据
输出:方向盘的角度 - 商品推荐
输入:使用者A,商品B的特性
输出:使用者A购买商品B的可能性

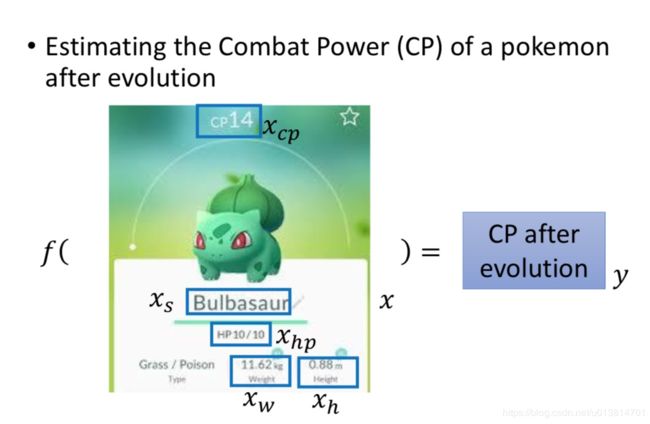
- pokemon的cp值
输入:进化前的CP、物种、血量、重量、高度等所有相关的信息
输出:进化后的CP值
这样来判断是否进化这只pokemon
模型步骤——机器学习三板斧
step1:模型假设,选择模型框架(线性模型)
step2:模型评估,如何判断众多模型的好坏(损失函数)
step3:模型优化,如何筛选最优的模型(梯度下降)
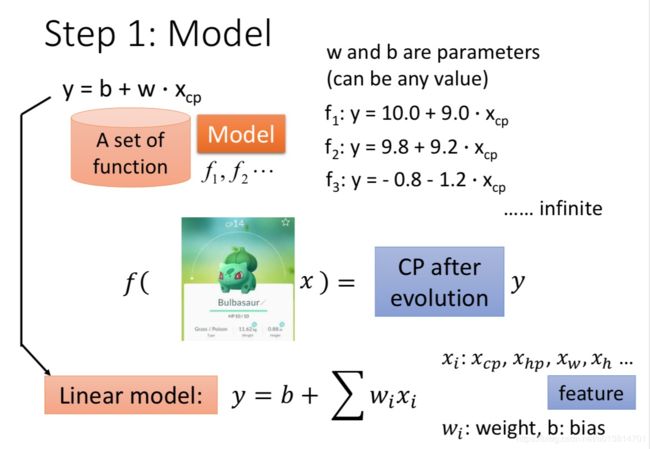
Step1: 模型假设 - 线性模型
一元线性模型(单个特征)
以一个特征 x c p x_{cp} xcp为例,线性模型假设 y = b + w ⋅ x c p y = b+w·x_{cp} y=b+w⋅xcp代表进化前的cp值,y是进化后的cp值,b 和 w是参数,可以是任何的数值。而且也是未知的,不同的b和w填进去就得到不同的function。
f 1 : y = 10.0 + 9.0 ⋅ x c p f_{1}:y=10.0+9.0⋅x_{cp} f1:y=10.0+9.0⋅xcp
f 2 : y = 9.8 + 9.2 ⋅ x c p f_{2}:y=9.8+9.2⋅x_{cp} f2:y=9.8+9.2⋅xcp
f 3 : y = − 0.8 − 1.2 ⋅ x c p f_{3}:y=−0.8−1.2⋅x_{cp} f3:y=−0.8−1.2⋅xcp
虽然可以做出很多的假设,但是在这个例子中,显然f3的假设不合理,进化后的cp值不能是负值。
总结:线性模型即为 y = b + ∑ ( w i ⋅ x i ) y = b+\sum(w_{i}·x_{i}) y=b+∑(wi⋅xi), x i x_{i} xi是输入x的一个属(feature), w i w_{i} wi称为权重(weight), b b b称为偏移(bias)。
Step2:模型评估 - 损失函数
收集和查看训练数据
接下来要**收集training data,才能找function。**找一分具体的杰尼龟的进化的例子。
x 1 x^{1} x1:用上标来表示一个完整的object的编号。
y ^ 1 \widehat {y}^{1} y 1:用^(读作head)来表示是真实值。
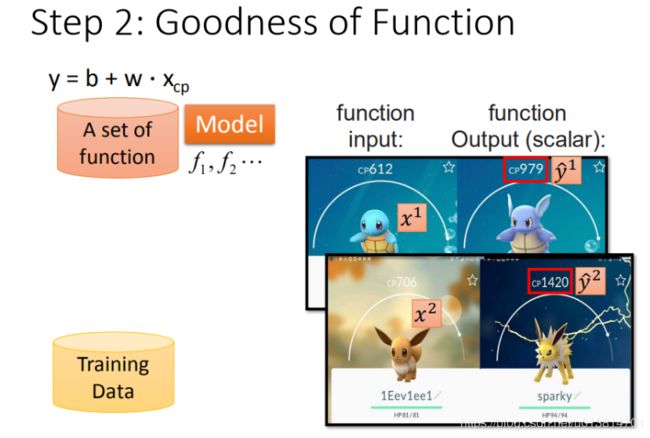
将10组原始数据在二维图中展示,图中的每一个点 ( x c p n , y ^ n ) (x^n_{cp},\widehat {y}^{n}) (xcpn,y n)对应着具体一只pokemon进化前的CP值 和 进化后的CP值。
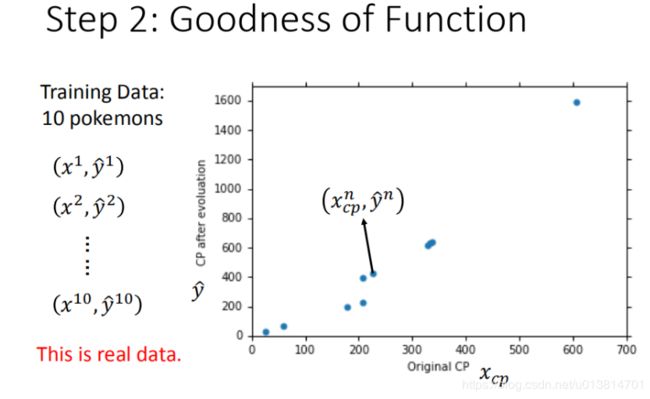
如何判断众多模型的好坏
有了这些真实的数据,那我们怎么衡量模型的好坏呢?
首先定义一个新的function,叫做loss function ,写作 L ( ) L() L()。这个函数用来衡量模型的好坏。他的输入也是一个function,也就是说loss function是function的function。输出是这个function有多不好。
对于这个例子中的loss function,输入的是model中的各个function,即为 L ( f ) L(f) L(f),而这些function又是通过w和b来定义的,所以也可以写成 L ( w , b ) L(w,b) L(w,b)。这样一来,也可以说是loss function在衡量一组参数(w和b)的好坏。
从数学的角度来讲,我们使用距离来表示误差。
- 在给定的w和b的情况下,首先可以确定用function输出值y【模型预测的CP值】和真实值ŷ【实际进化后的CP值】的差的大小来衡量模型的好坏,于是有 ( y ^ n − y n ) (\widehat{y}^{n}-y^{n}) (y n−yn)
- y = b + w ⋅ x c p y = b+w·x_{cp} y=b+w⋅xcp,所以有 ( y ^ n − ( b + w ⋅ x c p n ) ) \left( \widehat {y}^{n}-\left( b+w\cdot x^{n}_{cp}\right) \right) (y n−(b+w⋅xcpn))
- 为了保证距离都是正数,将结果开平方,有 ( y ^ n − ( b + w ⋅ x c p n ) ) 2 \left( \widehat {y}^{n}-\left( b+w\cdot x^{n}_{cp}\right) \right) ^{2} (y n−(b+w⋅xcpn))2
- 再把10组样本的误差加起来,有 L ( w , b ) = ∑ n = 1 10 ( y ^ n − ( b + w ⋅ x c p n ) ) 2 L\left( w,b\right) =\sum ^{10}_{n=1}\left( \widehat {y}^{n}-\left( b+w\cdot x^{n}_{cp}\right) \right) ^{2} L(w,b)=n=1∑10(y n−(b+w⋅xcpn))2

将 w , b w, b w,b 在二维坐标图中展示,如图所示:
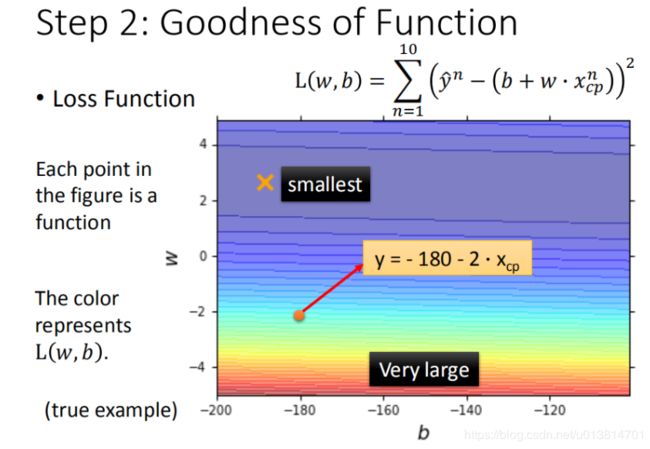
- 图中每一个点代表着一个模型对应的 w w w 和 b b b
- 颜色越偏红色代表模型越差,越偏蓝色代表模型越优
Step 3:最佳模型 - 梯度下降
如何筛选最优的模型(参数w,b)
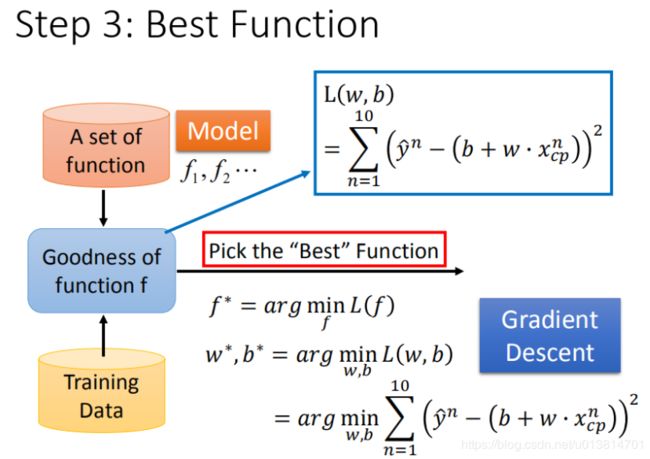
已知损失函数是 L ( w , b ) = ∑ n = 1 10 ( y ^ n − ( b + w ⋅ x c p n ) ) 2 L\left( w,b\right) =\sum ^{10}_{n=1}\left( \widehat {y}^{n}-\left( b+w\cdot x^{n}_{cp}\right) \right) ^{2} L(w,b)=∑n=110(y n−(b+w⋅xcpn))2需要找到一个最好的function,这个function就是令损失函数 L ( f ) L(f) L(f)结果最小的 f ∗ f^{*} f∗。
f ∗ = arg min f L ( f ) f^* =\mathop{\arg\min}\limits_{f}L(f) f∗=fargminL(f)
f f f又是由 w w w和 b b b来表示。所以也可以写成
w ∗ , b ∗ = arg min w , b L ( w , b ) = arg min w , b ∑ n = 1 10 ( y ^ n − ( b + w ⋅ x c p n ) ) 2 \begin{aligned} w^*,b^* &=\mathop{\arg\min}\limits_{w,b}L(w,b)\\ &=\mathop{\arg\min}\limits_{w,b}\sum ^{10}_{n=1}\left( \widehat {y}^{n}-\left( b+w\cdot x^{n}_{cp}\right) \right) ^{2} \end{aligned} w∗,b∗=w,bargminL(w,b)=w,bargminn=1∑10(y n−(b+w⋅xcpn))2
如果修过线代,则在知道十组 ( x c p n , y ^ n ) (x^n_{cp},\widehat {y}^{n}) (xcpn,y n)值的情况下,可以求出效果最好的 w , b w,b w,b的值。(p.s.老师原话,但是我咋不会呢?)
也有另外一种做法可以求出这个function,叫做梯度下降(gradient descent)。只要是可微分的function,梯度下降都可以来处理,找到可能是比较好的参数。
在实际的场景中,我们遇到的参数肯定不止 w , b w, b w,b。
只有一个参数
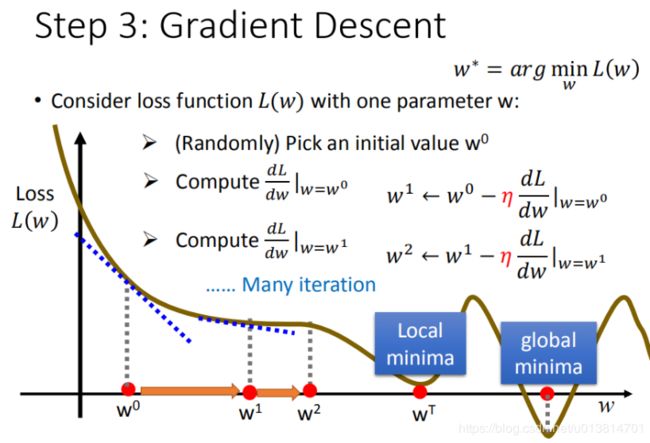
先从最简单的只有一个参数 w w w入手,定义 w ∗ = arg min w L ( w ) w^*=\mathop{\arg\min}\limits_{w}L(w) w∗=wargminL(w),则任务变成,找一个 w w w使得 L ( w ) L(w) L(w)的值最小。
最暴力的办法就是穷举 w w w,从无限小到无限大都带到 L ( w ) L(w) L(w)里面去,但是这样是没有效率的。
更聪明的办法是用梯度下降:
- 先随机选取一个点 w 0 w^0 w0(也有比较好的方法可以找到比较合适的点)
- 计算 w w w对 L L L在 w 0 w^0 w0处的微分
- 如果结果是负的,则应该向右移动,即增加 w w w的值;
- 如果结果是正的,则应该向左移动,即减少 w w w的值。
- 考虑增加/减少的量:一方面由微分值来确定,微分值越大,曲线越陡峭,移动的距离就越大,另一方面由一个常数项来决定,比如 η η η,称之为学习率(learning rate)或者步长。我们可以通过 η η η来控制每一步走的距离,既不要走太快,错过了最低点。同时也要保证不要走的太慢,导致太阳下山了,还没有走到山下。所以 η η η的选择在梯度下降法中往往是很重要的!这个量即为: η d L d ω ∣ w = w 0 η\dfrac {dL}{d\omega }|_{w=w^0} ηdωdL∣w=w0
- 根据第2步的描述,应该在梯度前添加一个负号,来满足朝着梯度相反的方向前进。梯度的方向实际就是函数在此点上升最快的方向!而我们需要朝着下降最快的方向走,自然就是负的梯度的方向,所以此处需要加上负号 − η d L d ω ∣ w = w 0 -η\dfrac {dL}{d\omega }|_{w=w^0} −ηdωdL∣w=w0
- 在本例中,应该向左移动得到新的 w w w: w 1 = w 0 − η d L d ω ∣ w = w 0 w^1 = w^0-η\dfrac {dL}{d\omega }|_{w=w^0} w1=w0−ηdωdL∣w=w0
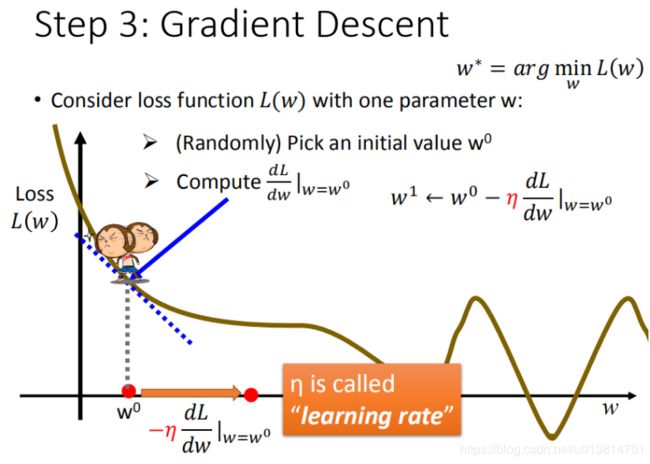
- 在 w 1 w^1 w1处重新计算一次微分值,值为负,则仍然应该向右移动,得到 w 2 w^2 w2
- 迭代下去,直到到达一个局部最优(local optimal),此时微分为0,无法再更新。但是极小值并不是全局最优(global optimal)。但是值得注意的是,在线性回归问题中,是没有局部最优的。
有两个参数
步骤:
- 随机选取两个初始值: w 0 , b 0 w_0,b_0 w0,b0
- 计算 w , b w,b w,b在 w 0 , b 0 w_0,b_0 w0,b0处对 L L L的偏微分: ∂ L ∂ w ∣ w = w 0 , b = b 0 , ∂ L ∂ b ∣ w = w 0 , b = b 0 \dfrac {\partial L}{\partial w}|_{w=w^0,b=b^0},\dfrac {\partial L}{\partial b}|_{w=w^0,b=b^0} ∂w∂L∣w=w0,b=b0,∂b∂L∣w=w0,b=b0
- 更新 w 1 , b 1 w^1,b^1 w1,b1
w 1 = w 0 − η ∂ L ∂ w ∣ w = w 0 , b = b 0 b 1 = b 0 − η ∂ L ∂ w ∣ w = w 0 , b = b 0 w^1 = w_0-\eta\dfrac {\partial L}{\partial w}|_{w=w^0,b=b^0} \\ b^1 = b_0-\eta\dfrac {\partial L}{\partial w}|_{w=w^0,b=b^0} w1=w0−η∂w∂L∣w=w0,b=b0b1=b0−η∂w∂L∣w=w0,b=b0 - 再计算 ∂ L ∂ w ∣ w = w 1 , b = b 1 , ∂ L ∂ b ∣ w = w 1 , b = b 1 \dfrac {\partial L}{\partial w}|_{w=w^1,b=b^1},\dfrac {\partial L}{\partial b}|_{w=w^1,b=b^1} ∂w∂L∣w=w1,b=b1,∂b∂L∣w=w1,b=b1
- 以此类推,直到找到一个相对小的梯度
梯度的定义及含义,以及关于梯度下降更加详细的解释,可以参考这篇文章:深入浅出–梯度下降法及其实现
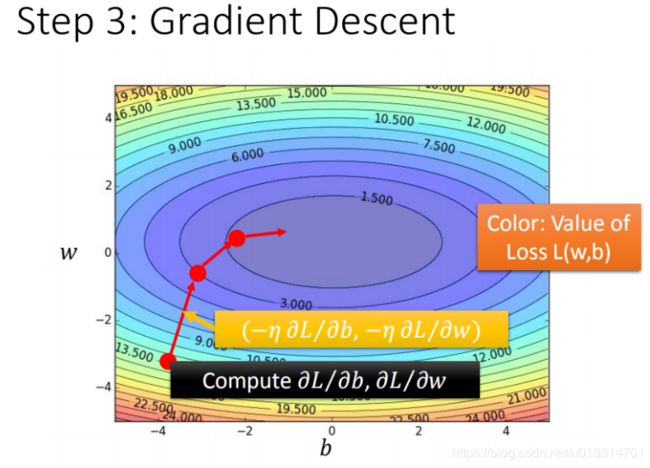
梯度下降推演最优模型的过程
- 每一条线围成的圈就是等高线,代表损失函数的值,颜色约偏蓝色的区域代表的损失函数越小
- 红色的箭头代表等高线的法线方向,这个方向是梯度的负方向(二元以上参数的梯度是向量,是有方向的)
梯度下降算法在现实世界中面临的挑战
我们通过梯度下降gradient descent不断更新损失函数的结果,这个结果会越来越小,那这种方法找到的结果是否都是正确的呢?
当前最优问题
梯度下降法选择的不一定是全局最优,起始点不同很可能结果不同。但是线性回归中,loss function都是凸面的,参考上图中,等高线都是同心圆,并没有局部最优。
外,还有没有其他存在的问题呢?
其实还会有其他的问题:
问题1:当前最优(Stuck at local minima)
问题2:等于0(Stuck at saddle point)
问题3:趋近于0(Very slow at the plateau)
注意:其实在线性模型里面都是一个碗的形状(山谷形状),梯度下降基本上都能找到最优点,但是再其他更复杂的模型里面,就会遇到 问题2 和 问题3 了
w和b偏微分的计算方法

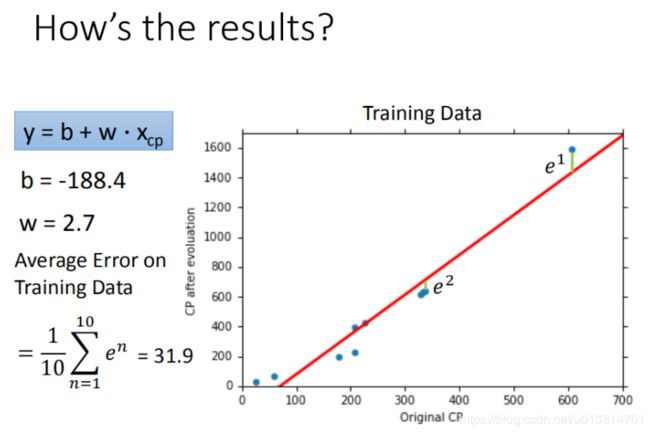
将最后计算得到的 w w w和 b b b带回到之前不确定参数的model当中,就得到最佳的function。计算得到 b = − 188.4 , w = 2.7 b=-188.4,w=2.7 b=−188.4,w=2.7。
如何验证训练好的模型的好坏
使用训练集和测试集的平均误差来验证模型的好坏
我们使用10组原始数据,训练集求得平均误差为31.9,如图所示:
 然后再使用10组Pokemons测试模型,测试集求得平均误差为35.0 如图所示:
然后再使用10组Pokemons测试模型,测试集求得平均误差为35.0 如图所示:
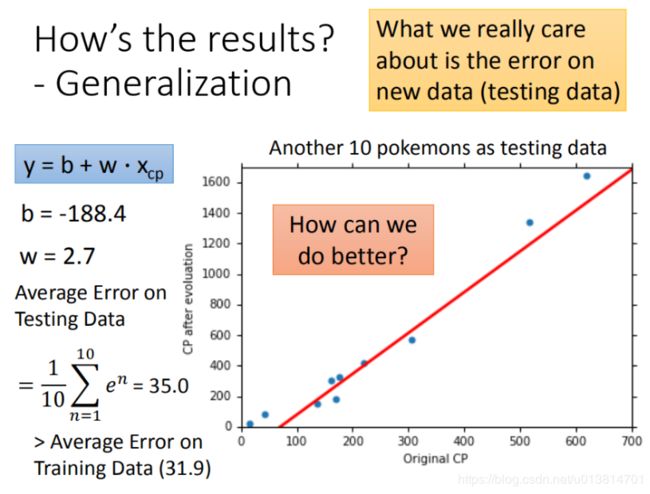
很明显,函数的泛化能力不太满意,但是也可以理解,毕竟是用的前10组数据训练得到,对前10组数据的拟合程度会更好。如果想做到更好,可能需要重新设计model,需要一个更复杂的model。
更强大复杂的模型:1元N次线性模型
在模型上,我们还可以进一部优化,选择更复杂的模型,使用1元2次方程举例,发现训练集求得平均误差为15.4,测试集的平均误差为18.4
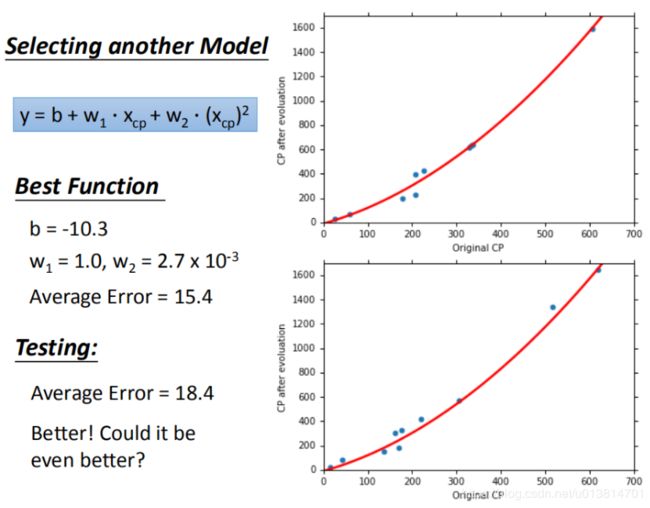
还可以变成一元三次方程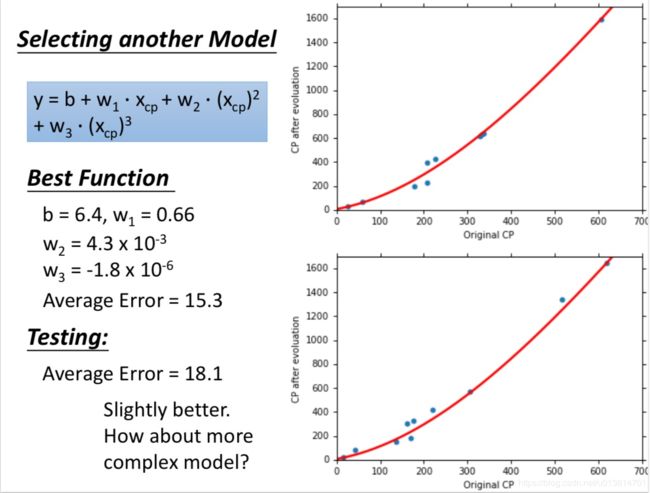
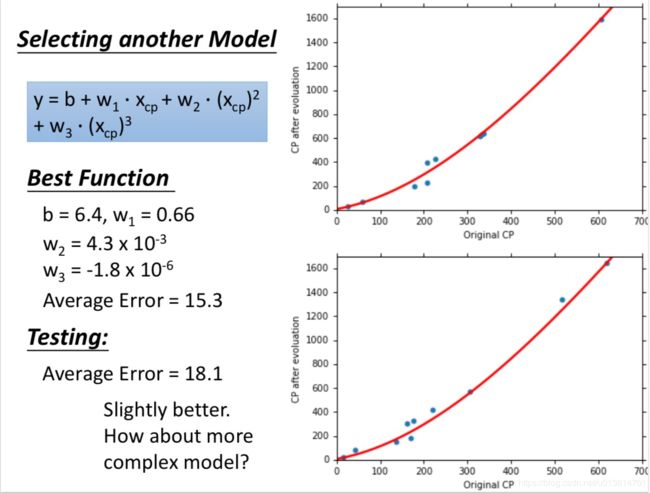
过拟合问题出现
再试试一元四次方程
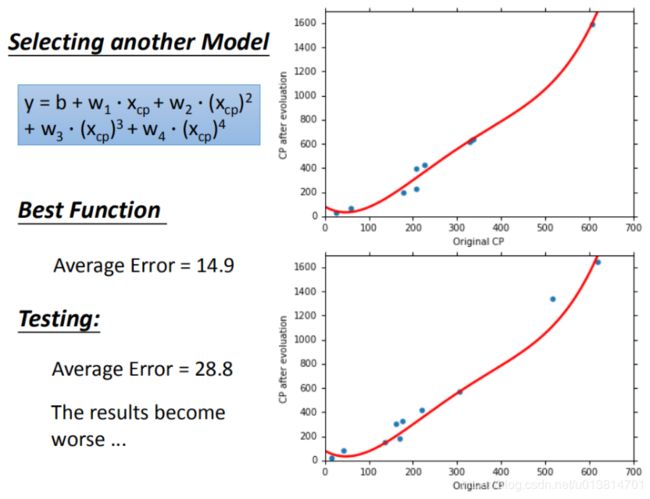
拟合结果不如一元三次方程,泛化能力下降。再试试一元五次方程

这个图线就nm离谱,都有负的预测值了。
在训练集上面表现更为优秀的模型,为什么在测试集上效果反而变差了?这就是模型在训练集上过拟合的问题。如图所示,每一个模型结果都是一个集合,5次模型包 ⊇ \supseteq ⊇ 4次模型 ⊇ \supseteq ⊇ 3次模型,所以在4次模型里面找到的最佳模型,5次模型肯定也考虑过了,所以5次模型给出的最佳模型,只可能比4次最佳模型的更好,就算保底也还是4次最佳模型。
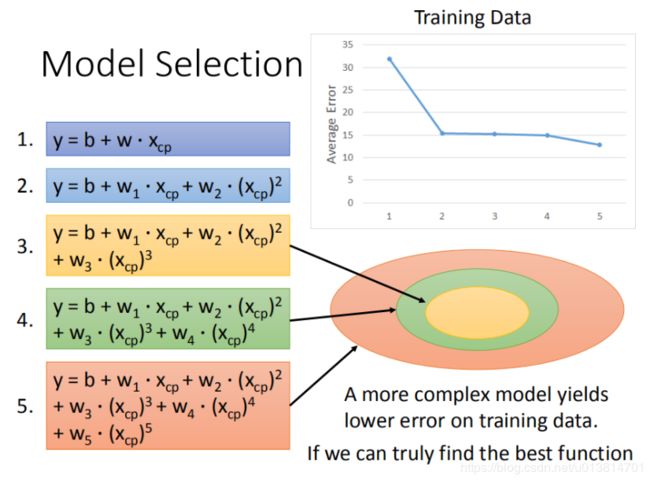
将错误率结果图形化展示,发现3次方以上的模型,已经出现了过拟合的现象:

这样看来,越复杂的model,泛化能力不一定越强。图中英文的含义是:更复杂的model并不总是能在训练集上得到更好的表现,这就是过拟合。所以我们要选择合适的model。
步骤优化
输入更多Pokemons数据,会发现有的pokemon有相同的起始CP值,但进化后的CP差距竟然是2倍。其实将Pokemons种类通过颜色区分,就会发现Pokemons种类是隐藏得比较深得特征,不同Pokemons种类影响了进化后的CP值的结果。
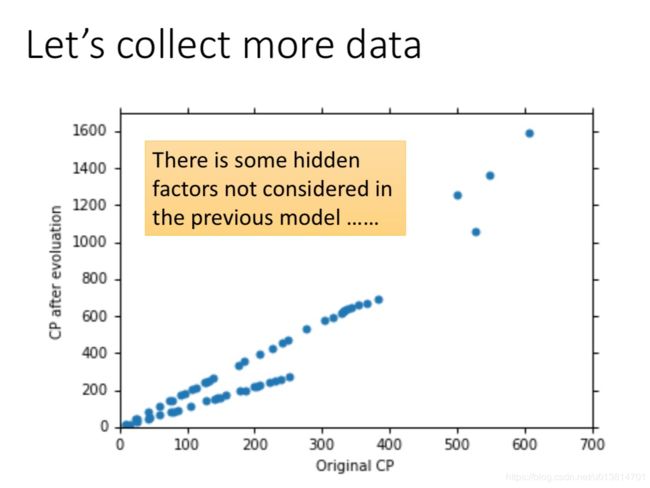

Step1优化:2个input的四个线性模型是合并到一个线性模型中
根据不同的物种,可以使用不同的模型
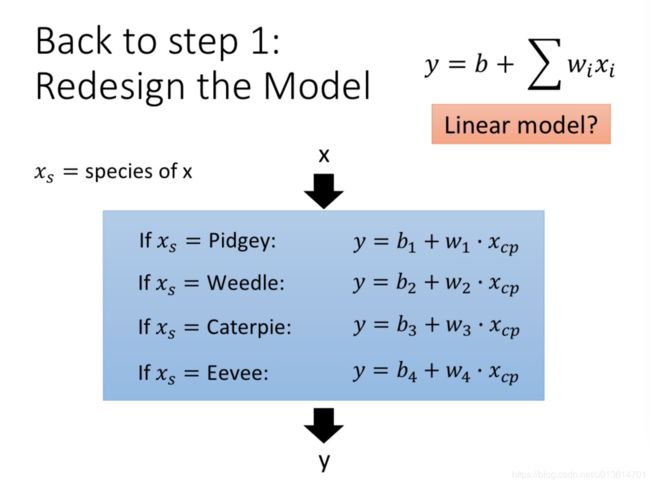
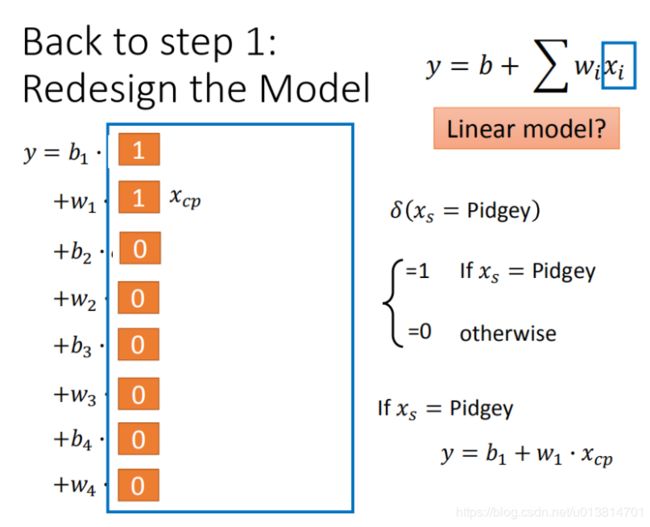
为了统一到一个线性模型里,可以这样写

物种来决定 δ \delta δ为1还是0。
结果如下图,泛化能力比之前的方法要好。
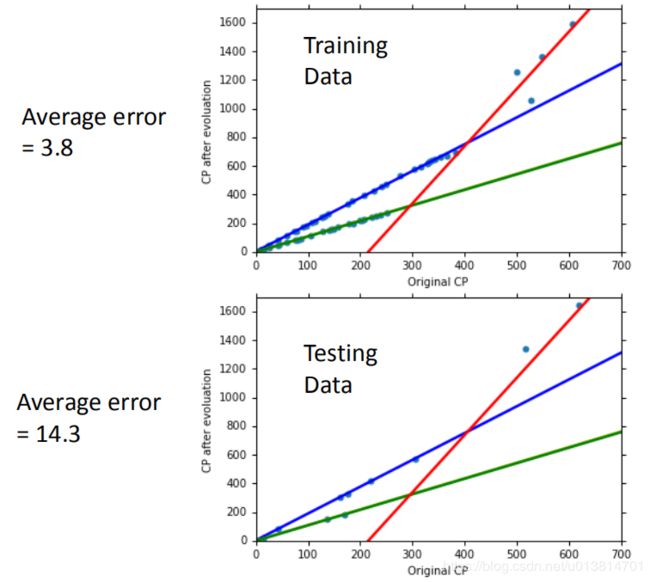
但是我们发现还是有点和直线还是有一些些没完全重合。也许还需要再多考虑一些参数。
Step2优化:如果希望模型更强大表现更好(更多参数,更多input)
在最开始我们有很多特征,图形化分析特征,将血量(HP)、重量(Weight)、高度(Height)也加入到模型中
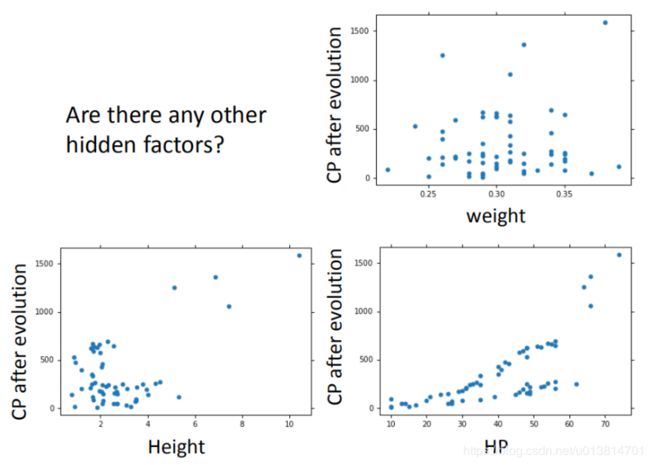
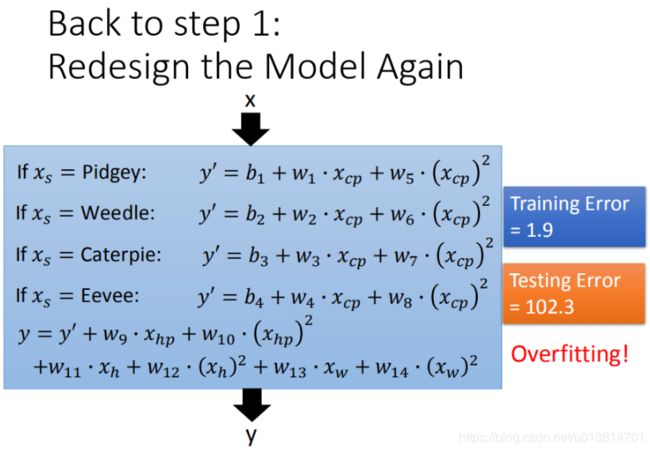
更多特征,更多input,数据量没有明显增加,但是泛化能力很差,仍旧导致overfitting。
Step3优化:加入正则化
更多特征,但是权重 w w w 可能会使某些特征权值过高,仍旧导致overfitting,所以加入正则化,在原来只有error部分的loss function的基础上增加正则化的部分(衡量function有多平滑)。
L = ∑ n ( y ^ n − ( b + ∑ w i x i ) ) 2 + λ ∑ ( w i ) 2 L =\sum _{n}\left( \widehat {y}^{n}-\left( b+\sum w_{i}x_{i}\right) \right) ^{2}+\lambda\sum(w_{i})^2 L=n∑(y n−(b+∑wixi))2+λ∑(wi)2
λ \lambda λ需要手动调整, w w w需要平方同样是为了保证结果为正。
目标同样还是求loss function最小时的参数,这样一来, w w w越小,loss function可能就会越小。但是为什么要期待参数 w w w尽可能小甚至是接近零的function呢?
小的 w w w意味着函数更平滑,也就是对输入值的变化不敏感。这样一来,输入的噪声也就会有更小的影响。而testing data就可以看做是对training data的噪声。在一定范围内,function越平滑,则function就越能在testing data上得到和training data相似的表现,模型泛化能力也就越强。

首先看 λ \lambda λ的变化对training data上的error部分的影响
随着 λ \lambda λ的增大,正则化系数(自己起的名字) λ ∑ ( w i ) 2 \lambda\sum(w_{i})^2 λ∑(wi)2的影响力增大,function越来越平滑,因为此时 w i w_i wi小的function才会容易被选出来。
同时,loss function中error部分的影响力会越小,error部分的值也必然会增大,因为此时选出来的 w i w_i wi并不一定是能让error最小的。
再看 λ \lambda λ的变化对testing data上的error部分的影响
随着 λ \lambda λ的增大,同样的,function越来越平滑。
刚开始,testing data的error部分的值开始缩小,这是得益于function越来越平滑,模型泛化能力也就越来越强。但是随着 λ \lambda λ的继续增大,error部分的影响力越来越小,虽然泛化能力越来越好,但是error部分本身也开始变大,模型对training data的误差越来越大,所以对testing data的误差也变得越来越大。此时的error又开始变大。
考虑平滑到极致的情况:假想 w w w无限接近0,function无限接近水平线,非常平滑,接近一条直线,但是已经不能去拟合training data里的数据了,loss function中的error部分会非常大。
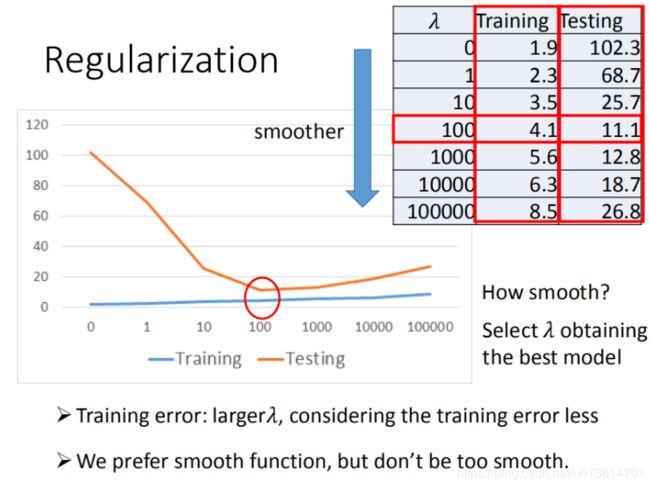
具体function该有多平滑,就变成在loss function中该怎么调 λ \lambda λ的问题。
值得注意的是,在正则化的loss function中并没有增加对 b ( b i a s ) b(bias) b(bias)的讨论。因为 b ( b i a s ) b(bias) b(bias)对function曲线的平滑程度没有影响,它只影响function的高低。