「百度之星」2020 - 初赛三题解

题目网址链接： 2020 年百度之星·程序设计大赛 - 初赛三

1001.Discount

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=6783

思路： 根据题目定义，找出最大的那个优惠比例即可

代码

#include 
#include 
#include 
#include 
#include 
#include 
#define ft first
#define sd second
#define pb push_back
#define nul string::npos
using namespace std;
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
const int maxn=1e2+7;
const db eps=1e-6;
const int inf=0x3f3f3f3f;
int t,n;
struct no{
    db b,c,w;
}p[maxn];
bool cmp(no x,no y){
    return x.w>y.w;
}
void solve(){
    scanf("%d",&n);
    for(int i=0;i<n;i++){
        scanf("%lf%lf",&p[i].b,&p[i].c);
        p[i].w=(1.0-p[i].c)/(p[i].b+1.0-p[i].c);
    }
    sort(p,p+n,cmp);
    printf("%.5f\n",p[0].w);
}
int main(){
    cin>>t;
    while(t--)solve();
    return 0;
}

1002. Game

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=6784

思路： 显然 $p>1$ 的时候，Alice拿的是多的那一堆儿，肯定不用换，不然就无法确定自己是哪一堆儿，但是结果无非两种，要么翻倍，要么减半，所以期望值是：$2p\ast 0.5+0.5p\ast 0.5=1.25p>p$，交换的期望值大于不交换的，所以应该交换

代码

#include 
#include 
#include 
#include 
#include 
#include 
#define ft first
#define sd second
#define pb push_back
#define nul string::npos
using namespace std;
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
const int maxn=1e2+7;
const db eps=1e-6;
const int inf=0x3f3f3f3f;
int t;
int sgn(db x){
    if(abs(x)<eps)return 1;
    else if(x>eps)return 0;
    return 1;
}
void solve(){
    db p;
    scanf("%lf",&p);
    if(sgn(p-1.00000))puts("Yes");
    else puts("No");
}
int main(){
    cin>>t;
    while(t--)solve();
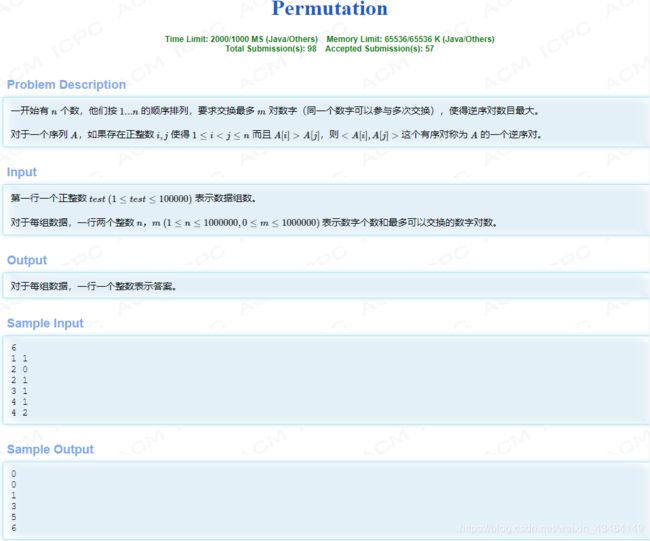
    return 0;
}

1003. Permutation

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=6785

思路： 首先我们应该可以发现，无论交换多少对，肯定是：$(1,n),(2,n-1),...$ 这样的顺序交换会使逆序对数最大化。所以，如果 $m\ge \lfloor \frac{n}{2}\rfloor$ ，那么就能使原序列递减，逆序对数最多：$\frac{n(n-1)}{2}$，否则，我们就分段去计算逆序对数即可，比如说一开始序列为：$1,2,3,...,n-1,n$，按照最优方法交换完 $m$ 对数后，序列为：$n,n-1,...,n-m+1,m+1,m+2,...,n-m,m,m-1,...,2,1$，很显然分成了三段，第一段是：$n,n-1,...,n-m+1$，他们最大，所以构成的逆序对数为：$\frac{(n-m+n-1)m}{2}$；第二段为：$m+1,m+2,...,n-m$,这段递增，但是他们每个数都大于第三段的任何一个数，所以这段构成的逆序对数为：$(n-2m)m$；第三段为：$m,m-1,...,2,1$，这段也是递减，所以构成的逆序对数为：$\frac{(m-1)m}{2}$，这三段的逆序对数相加即可。

代码

#include 
#include 
#include 
#include 
#include 
#include 
#define ft first
#define sd second
#define pb push_back
#define nul string::npos
using namespace std;
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
const int maxn=1e2+7;
const db eps=1e-6;
const int inf=0x3f3f3f3f;
int t;
int n,m;
void solve(){
    scanf("%d%d",&n,&m);
    ll ans=(ll)n*(n-1)/2;
    if(m>=n/2){
        printf("%lld\n",ans);
        return ;
    }
    ans=((ll)n*2-m-1)*m/2+(ll)(n-2*m)*m+(ll)(m-1)*m/2;
    printf("%lld\n",ans);
}
int main(){
    cin>>t;
    while(t--)solve();
    return 0;
}

1004. Intersection

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=6786

思路： 我的策略是，直接看两个车道最后一辆车，首先看右车道最后一辆车即将通过(还剩1秒通过)时，左边最后一辆车的位置，然后根据其所在位置来判断还需要多长时间才能通过，前面的车大可不必考虑，因为，只要最后一辆车能通过，前面的肯定也都通过了。

代码

#include 
#include 
#include 
#include 
#include 
#include 
#define ft first
#define sd second
#define pb push_back
#define nul string::npos
using namespace std;
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
const int maxn=1e5+7;
const db eps=1e-6;
const int inf=0x3f3f3f3f;
int T;
int n,m;
int a[maxn],b[maxn],a1,b1;
void solve(){
    a1=b1=0;
    scanf("%d",&n);
    for(int i=1,op,pos;i<=n;i++){
        scanf("%d%d",&op,&pos);
        if(op==1)b[b1++]=pos;
        else a[a1++]=pos;
    }
    sort(a,a+a1);
    sort(b,b+b1);
    if(b1==0){
        int t=2+a[a1-1];
        printf("%d\n",t);return;
    }
    int t=b[b1-1]+1;
    if(a1==0||t>=a[a1-1]+3){
        printf("%d\n",t);return;
    }
    int apos=a[a1-1]-t+1;
    if(apos<=0)t++;
    else t+=1+apos;
    printf("%d\n",t);
}
int main(){
    cin>>T;
    while(T--)solve();
    return 0;
}

1005. Chess

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=6787

思路： 考虑用动态规划来解这道题，定义状态：$dp[i][j][k]$ 表示到第 $i$ 个格子时，已经用了 $j$ 个传送器，并且包含第 $i$ 个格子在内已经安置了连续 $k$ 个传送器。由于第1个格子不能放传送器且不能连续11个位置放传送器，所以可以得出状态转移方程为：
当 $k$ 为 $0$ 时： $dp[i][j][k]={\sum }_{0\le k^{\prime }\le 10}dp[i-1][j][k^{\prime }]$
当 $k$ 非 $0$ 时： $dp[i][j][k]=dp[i-1][j-1][k-1]\times (i-1)$
之所以是 $i-1$ 是因为除了第 $i$ 个格子以外的其他的 $i-1$ 个格子都可以是传送器传送的位置

代码

#include 
#include 
#include 
#include 
#include 
#include 
#define ft first
#define sd second
#define pb push_back
#define nul string::npos
using namespace std;
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
const int maxn=1e3+7;
const int mod=1e9+7;
const int inf=0x3f3f3f3f;
int T,n,m;
int dp[maxn][maxn][12];
void init(){
    dp[1][0][0]=dp[2][0][0]=1;
    for(int i=2;i<=1000;i++){
        for(int j=0;j<i;j++){
            for(int k=0;k<=min(10,j);k++){
                if(k)dp[i][j][k]=(ll)dp[i-1][j-1][k-1]*(i-1)%mod;
                dp[i+1][j][0]=((ll)dp[i+1][j][0]+dp[i][j][k])%mod;
            }
        }
    }
}
void solve(){
    scanf("%d%d",&n,&m);
    int ans=dp[n][m][0]>0?dp[n][m][0]:-1;
    printf("%d\n",ans);
}
int main(){
    init();
    cin>>T;
    while(T--)solve();
	return 0;
}

1006. Ant

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=6788

思路： 看了官方题解大概理解了一些，官方题解说：“第一只蚂蚁走的路要不是直接走向石榴，要不最多在一个点有一个分叉，那么我们只要把石榴到根的路径记下来，枚举一下分叉在哪里，然后把概率算出来就可以了”。首先不妨设 $1-m$ 的路径为关键路径，$1-m$ 上的点为关键点。第二只蚂蚁到达 $m$ 点的前提是第一只蚂蚁最终也到了 $m$ 点，所以可以把第二只蚂蚁走最短路到达 $m$ 点的概率分成了两部分，第一部分当然就是第一只蚂蚁直接走最短路到达石榴的概率，要不然就是第一只蚂蚁可能会拐弯，但是如果从根出发往下走的话，在走的过程中不会再往回拐，因为往回拐就回不来了，也就到达不了 $m$ 点了，所以第一只蚂蚁只可能在关键路径 $1-m$ 上的除 $m$ 点外，每个关键点往其他儿子上拐，把这个概率用简单迭代算出来就行了，需要特判一下 $m$ 点在根的情况。由于从根开始计算的概率和从 $m$ 点计算是相同的，所以不妨就从 $m$ 点开始往根的方向计算概率，因为这个路径很容易记录，但是反过来就很麻烦。

代码

#include 
#include 
#include 
#include 
#include 
#include 
#define ft first
#define sd second
#define pb push_back
#define nul string::npos
using namespace std;
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
const int maxn=1e5+7;
const int mod=1e9+7;
const int inf=0x3f3f3f3f;
int T,n,m;
vector<int> g[maxn];
int f[maxn],son[maxn];
ll qpow(ll x,ll y,ll mod){
    ll res=1; x%=mod;
    while(y){
        if(y&1)res=res*x%mod;
        x=x*x%mod;
        y>>=1;
    }
    return res;
}
ll inv(ll a,ll p){
    return qpow(a,p-2,p)%p;
}
void init(){
    for(int i=1;i<=n;i++){
        g[i].clear();
    }
}
void dfs(int u,int fa){
    son[u]=0;
    f[u]=fa;
    for(auto v: g[u]){
        if(v==fa)continue;
        dfs(v,u);
        son[u]++;
    }
}
void solve(){
    scanf("%d%d",&n,&m);
    init();
    for(int i=1,u,v;i<n;i++){
        scanf("%d%d",&u,&v);
        g[u].pb(v);
        g[v].pb(u);
    }
    if(m==1){
        puts("1");
        return;
    }
    dfs(1,0);
    ll a=1,b=0;
    for(int i=f[m];i!=0;i=f[i]){
        int tmp=(i!=1);
        a=a*inv(son[i]+tmp,mod)%mod;//第一只蚂蚁走关键路径的概率
        b=b*inv(son[i]+tmp,mod)%mod;
        //第一只蚂蚁拐弯的概率
        b=(b+a*inv(son[i]-1+tmp,mod)%mod*(son[i]-1)%mod)%mod;
    }
    printf("%d\n",(int)((a+b)%mod));
}
int main(){
    cin>>T;
    while(T--)solve();
	return 0;
}

1007. Fight

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=6789

思路： 直接枚举Mr Left和Mr Mid的对局次数，这个次数固定后是可以直接算出两个人还剩多少血量的，最后是再分两种情况考虑：Mr Right先和Mr Left对决，然后和Mr Mid对决，或者说Mr Right先和Mr Mid对决，然后和Mr Left对决，看哪个的对决总次数会更少，取最小即可。中间会有很多细节要处理(比赛时细节没处理好，草率了)，比如对决后两者血量都不大于0了，将要对决之前其中一者血量不大于0，这些都要考虑在内。

 

代码

#include 
#include 
#include 
#include 
#include 
#include 
#define ft first
#define sd second
#define pb push_back
#define nul string::npos
using namespace std;
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
const int maxn=1e5+7;
const int mod=1e9+7;
const int inf=0x3f3f3f3f;
int T;
int x,y,z;
void solve(){
    scanf("%d%d%d",&x,&y,&z);
    int ans=inf;
    for(int xy=0;xy<=min(1000/x+(1000%x!=0),1000/y+(1000%y!=0));xy++){
        int xx=1000,yy=1000,zz=1000;
        xx-=xy*y,yy-=xy*x;
        int xz=0,yz=0;
        if(xx<=0&&yy<=0)ans=min(ans,xy);
        else if(xx>=yy){
            xz=min(xx/z+(xx%z!=0),zz/x+(zz%x!=0));//先xz的情况
            if(yy<=0){
                ans=min(ans,xy+xz);
                continue;
            }
            int xxx=xx-xz*z,zzz=zz-xz*x;
            if(xxx<=0&&zzz<=0)ans=min(ans,xy+xz);
            else {
                if(xxx<=0){
                    xz+=min(yy/z+(yy%z!=0),zzz/y+(zzz%y!=0));
                    ans=min(ans,xy+xz);
                }
            }
            yz=min(yy/z+(yy%z!=0),zz/y+(zz%y!=0));//先yz的情况
            int yyy=yy-yz*z;zzz=zz-yz*y;
            if(yyy<=0&&zzz<=0)ans=min(ans,xy+yz);
            else {
                if(yyy<=0){
                    yz+=min(xx/z+(xx%z!=0),zzz/x+(zzz%x!=0));
                    ans=min(ans,xy+yz);
                }
            }
        }
        else {
            yz=min(yy/z+(yy%z!=0),zz/y+(zz%y!=0));//先yz的情况
            if(xx<=0){
                ans=min(ans,xy+yz);
                continue;
            }
            int yyy=yy-yz*z,zzz=zz-yz*y;
            if(yyy<=0&&zzz<=0)ans=min(ans,xy+yz);
            else {
                if(yyy<=0){
                    yz+=min(xx/z+(xx%z!=0),zzz/x+(zzz%x!=0));
                    ans=min(ans,xy+yz);
                }
            }
            xz=min(xx/z+(xx%z!=0),zz/x+(zz%x!=0));//先xz的情况
            int xxx=xx-xz*z;zzz=zz-xz*x;
            if(xxx<=0&&zzz<=0)ans=min(ans,xy+xz);
            else {
                if(xxx<=0){
                    xz+=min(yy/z+(yy%z!=0),zzz/y+(zzz%y!=0));
                    ans=min(ans,xy+xz);
                }
            }
        }
    }
    cout<<ans<<'\n';
}
int main(){
    cin>>T;
    while(T--)solve();
	return 0;
}

1008. Graph

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=6790

思路： 待补

代码