牛客多校7 - A National Pandemic(树链剖分+线段树)

题目链接：点击查看

题目大意：给出一棵树，再给出 m 次操作，每次操作分为三种类型，dist( x , y ) 代表点 x 和点 y 之间的距离：

1. 1 pos val：将点 pos 位置的值增加 val ，将其余所有点 x 的值，增加 val - dist( pos , x )
2. 2 pos：点 pos 位置的值与 0 取 min
3. 3 pos：查询点 pos 位置的值

题目分析：参考博客：https://blog.csdn.net/tianyizhicheng/article/details/107734665

第二个操作显然是充数的，额外用一个 delta 数组随便维护一下就好了，主要是操作 1 和操作 3

对于每次操作 1 来说，肯定不能暴力去维护所有的 n 个点，所以我们不妨将点权转换为每个点与 root 节点（ 设为点 1 ）的相对权值

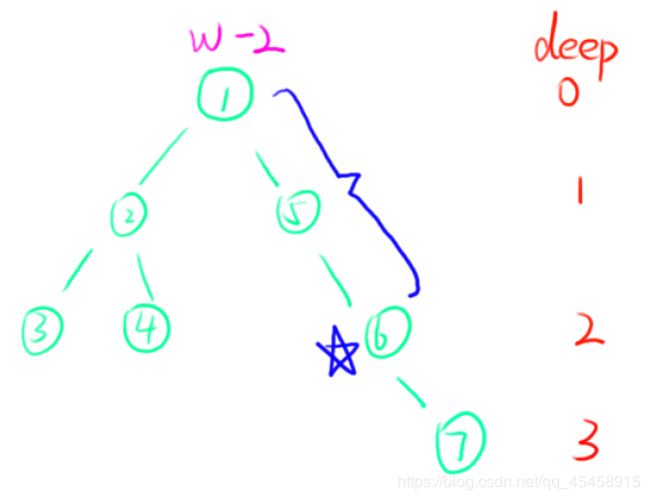
画个图然后分类讨论一下吧，现在假设我们将点 6 的权值增加 w，那么显然根节点（点1）的权值会增加 w - 2 ，我们将点 1 的权值记为 all ，此时也就是 all = w - 2，因为点 6 的深度为 2

如果我们想要求与点 6 的 lca 为 root 的点的权值，也就是点 1 , 2 , 3 , 4 的权值，显然 all - deep[ x ] 就是答案了，因为 lca 为 1 ，所以这些点与点 1 的距离增大，相应的与点 6 的距离也会增大，答案自然也会变小

既然我们想让答案与 deep 形成关系，对于那些，与点 6 的 lca 不为 root 的点，如：点 5 , 6 , 7 ，也需要构造一个公式，也就是 all - deep[ x ] + y 为点 x 的权值，通过观察不难发现，这个 y 值可以分两种情况讨论：

1. 当点 x 位于 点 1 ~ 点 6 的路径上，即点 5 和 6 ，那么 y 的值为点 1 ~ 点 x 的边数 * 2
2. 否则，y 的值为点 1 ~ 点 6 的边数 * 2

综上所述，对于操作 1 来说，需要执行的操作就是：

1. all += w - deep[ x ]
2. 将点 1 ~ 点 x 这条路径上的边权 + 2

对于操作 3 查询来说，答案就是 all + ( 点 1 ~ 点 x 这条边上的边权之和 ) - deep[ x ] * num

注意，这里的 deep 为什么突然乘以 num 了，解释一下这个突然出现的 num ，其意义是操作 1 的数量，举个很简单的例子，还是上图，如果对点 6 进行两次操作 1 ，增加的权值都是 w ，那么此时的 all = ( w -  2 ) * 2 ，如果要求点 2 的权值，答案应该是 all - deep[ 2 ] * 2 而不是 all - deep[ 2 ]

剩下的就是实现了，对于树上路径的区间更改和区间查询，可以利用树链剖分和线段树来执行，因为是要对边权操作，所以可以将边权转换为点权，很基本的操作，直接实现就好了

操作 2 的 delta 就不多说了，如果操作 1 明白了的话，操作 2 看一眼代码应该就会了

代码：
 

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include