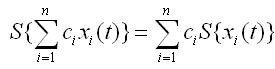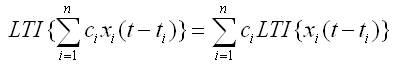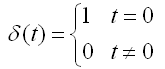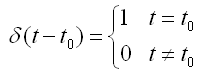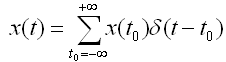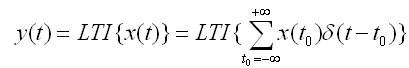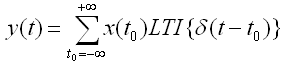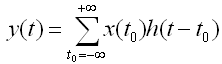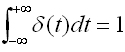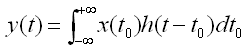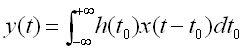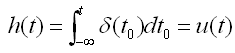信号系统与卷积

    在不少程序员眼中，卷积这个数学概念是很神秘很难懂的。由于其在数学、物理学、电子工程、信号处理、计算机科学中极为重要，所以我试图在本文中讲解卷积的概念，力求易读易懂，让尽可能多的人理解卷积。

 

    前几天见到VC知识库论坛上有人提问：“卷积是什么意思？”，似乎女友也问过类似问题，所以我想很有必要澄清这个既基础又重要的卷积概念。如果您已经对此非常了解，那完全可以忽略本文了。本文的目标读者是那些见了卷积这两个字就头大，又迫于工作需要，必须弄懂的人。我假设您已经通过了大学一年级的高数考试，但现在已经忘得差不多了J。很多教科书一上来就会给出卷积的定义，接着就是一串推导、证明、例子，如果你不太适应这种方式，那本文可能会非常适合你。

 

    卷积在信号处理领域中尤为常用，就以此慢慢引入卷积概念吧。日常生活中到处都是信号系统，它们接受一定的输入后，会给出一定的输出：手机受到对方来电的信号就会响铃或震动；电脑接到一串按键信号，屏幕就会输出一串对应的字符；女友在收到男友送的一束玫瑰后也许会送上一个热吻……现在，我们把这些信号系统抽象成“黑匣子”，不管它的内部构造，而只关注它对输入的响应。

 

    数学化一点儿，将一个给定的信号系统记为S，设输入信号为x(t)，输出信号为y(t)，t可以代表时间，也可以是其它什么。那么：y(t) = S{ x(t) }就表示系统S将x(t)这个输入信号转化为输出信号y(t)。太一般化的信号系统不容易研究，那就加入一些“合理的”限制条件。S是连续（continuous）的，如果t可以连续变化；特别的，x(t)和y(t)都是定义在实数域上的函数。物理世界中的信号系统大多是连续的。S是离散（discrete）的，如果t只能取一些分立的值；特别的，x(t)和y(t) 都是定义在整数域上的函数。离散的信号系统可以比较方便的被计算机分析处理。S是线性（linear）的，如果对任意两个输入信号x₁、x₂和任意的常数c₁和c₂有：

S{ c₁x₁(t) + c₂x₂(t) } = c₁S{ x₁(t) } + c₂S{ x₂(t) }

    拿超市作比喻，我跟女友去买2斤萝卜和3斤白菜，即c₁=2，c₂=3，x₁是萝卜，x₂是白菜。如果超市是“线性的”，那么无论是我俩合一块结帐，还是各拿一样菜从两个收银通道分别结帐，最终花的钱是一样多的。更一般的，对任意n个输入信号x_n，有：  

 c_i为任意常数。S是时间不变（time-invariant）的，如果对任意的常数t₀，有y(t – t₀) = S{ x(t - t₀) }。意思是说，如果输入信号迟到t₀的时间，那么我们还是会得到相同的输出，只是输出也晚了t₀的时间。还拿超市作比喻，我今天花了40块钱买桶食用油。如果超市是“时间不变”的，那我过两天再去买同样的东西照样是花40块钱，只不过是晚了两天才拿到而已。如果S同时具备线性和时间不变性，则称之为线性时不变系统，记作LTI，它满足：

其中x_i为任意输入，c_i，t_i为任意常数。（如果某个延迟t_i < 0，意思是未来的信号提前影响系统。我们并未要求系统是因果性（causal）的，即允许未来的信号对当前的系统输出产生影响。）

 

    本文将对比讨论离散的和连续的线性时不变系统。前者更容易理解，就先讲离散的线性时不变系统吧。有了前文给系统加入的约束，我们就凭空获得了一些已知条件。为了进一步简化问题，这次我们拿输入信号开刀，将之限定为一个最简单的单位强度的脉冲输入。说白了就是轻轻碰你一下，看看有啥反映。这个输入叫做离散冲击函数（impulse function）：

 

t是整数。它只在原点处有非零值，其余地方全是0。由定义显然： 

t₀是任意整数常数。这个函数具有筛选特性（sifting property）：

    这看起来是很显然的。你可能会问：“这玩意儿有什么用？我们可以从已知函数x和d来构造新函数x，这简直是循环论证，而且还引入了如此复杂的额外步骤。”其实，上式的含义是把x(t)看作是一系列常数，就像c_i那样，不再依赖于t。于是我们就把输入信号x(t)分解成了一串带有不同系数的冲击信号的叠加。

 

     LTI系统对冲击函数的响应（即输出）叫做冲击响应（impulse response）：h(t) = LTI{ d(t) }。可以证明，对于一个LTI系统，只要我们知道了冲击响应函数h(t)，就可以计算出它对任意输入的响应。换句话说，如果我们能够分析出一个LTI系统对单位强度的脉冲信号所做出的响应，那么我们就可以完全（至少是从输入输出的角度）描述此系统的行为了。

 

    下面来证明看看。一个LTI系统对于任意输入的响应为：

由于系统是线性的，所以上式可变为：

 

仔细看看，其中的LTI{ d(t – t₀) }就是系统对冲击函数的响应，只不过推迟了t₀而已。由于系统是时间不变的，所以LTI{d(t - t₀)} = h(t – t₀)。（顺带提一句，如果系统是因果性的，则任何的输出都必须起因于现在和过去的输入，与将来无关，那么对于所有的t < 0，有h(t) = 0）。将其代入得到最终的关系式：

这就是卷积（convolution）！值得注意的是，上述推倒过程只用到了线性和时间不变性公理，与富利叶变换无关（那是在这以后的理论了）。

 

    对于连续的LTI系统，证明的步骤跟离散的情况如出一辙，只不过冲击函数需要重新定义了。我们要构造这样一个脉冲输入，它只持续极短的时间（这在离散情形下是自然而然的），但其这个输入又要足够的强，以便系统会做出反应。这个输入的数学形式就是Dirac delta函数d(t)（严格说来它不是一个真正的函数，而是一个分布（distribution）。当初很多数学家对这个由物理学家和工程师们草草引入的东西非常反感[注1]）。Dirac delta函数没法直接定义，只能从侧面给出它的两个性质：

对于任意的t ≠ 0，有d(t) = 0，

而且    （此处也是数学家们认为最具争议之处）

可见Dirac delta函数除t = 0以外处处为0，但其函数曲线与t轴所围成的面积为1。Dirac delta函数可以看成是一个积分面积为1的，仅在原点附近有非零值的函数，被逐渐从两侧挤扁，同时保持积分面积不变。当它被挤成在t = 0的一条高高的直线时，就得到了真正的Dirac delta函数。

 

Dirac delta函数的筛选特性为：

 

于是，对于连续的LTI系统，其对任意输入的响应为：

因为系统是线性的，所以：

再由时间不变性，LTI{d(t - t₀)} = h(t – t₀)，代入上式就得到了连续LTI系统下的卷积：

只要做一个简单的积分变量替换，就会得到另一个等价形式：

    无论离散的还是连续的LTI系统，其滤波特性完全由h(t)描述，不同的LTI系统拥有不同的h(t)。举些例子吧。当你输入函数为x(t) = d(t)时，算出的y(t) = h(t)，正好是冲击响应函数，这也验证了前面的推导是自洽的。假如已知h(t) = 3d(t)，那么y(t) = 3x(t)，即这是一个理想放大器，信号增益为3倍；而h(t) = d(t)的系统则相当于导线。假如已知：

即这是个积分系统，输出为之前输入信号的强度的累积。可以求得此系统的冲击响应函数为：

正好是一个在原点的单位阶梯函数。

 

    至此，我们比较完整的推导了线性时不变系统的输入输出的关系式。只要获得冲击响应函数，就可求出系统对任意输入的响应，而这个输出函数正好等于冲击响应函数与输入函数的卷积。

 

[注1：Dirac delta函数是极限情况下的渐进函数，在真实世界中是无法构造一个真正的Dirac delta函数形式的输入信号的。另外Dirac delta函数只有在积分时才有意义。虽然工程师们大大咧咧的在非积分表达式中也使用Dirac delta函数，但最终这些表达式都会以积分的方式被真正的求值。也许理解Dirac delta函数的最好方式是理解黎曼积分（Riemann Integral）与勒贝格积分（Lebesgue Integral）的不同。但对于真实的物理系统，二者得到同样的结果，只不过数学上的处理手法大相径庭而已。]