多视图几何总结——基础矩阵、本质矩阵和单应矩阵的求解过程

多视图几何总结——基础矩阵、本质矩阵和单应矩阵的求解过程

在《视觉SLAM十四讲》中，仅仅给出了基础矩阵、本质矩阵和单应矩阵的推导过程，并没有详细给出其求解过程，再看过《计算机视觉中的多视图几何》之后才发现这里面原来有这么多巧妙的地方，因此在这篇文章中予以总结。

1. 说明——其实求解过程大同小异

为什么说求解过程大同小异呢，不管是那种矩阵，在求解方法的分类上大致是都可以分为基于代数误差的线性估计和基于几何误差的非线性估计，在基于代数误差的线性估计中，不管是那种矩阵最后的形式一般都是$$Ax=b$$其中$A$是由匹配的点构成的矩阵，而$x$是由待解的基础矩阵或者单应矩阵的元素构成的向量，$b$是根据解法的不同而不同，在基于几何误差的非线性估计中，又几乎都有黄金标准方法（重投影误差）和一阶几何误差（Sampson距离）等方法，因此我个人觉得是比较相似的，因此，我下文主要是单应矩阵的求解过程详解，其他矩阵主要说明不同。

2. 单应矩阵求解过程

2.1 基于代数误差的线性估计

首先我们知道，单应矩阵的对应点的方程为：$$H{x}_i=x_i^{\prime }$$其中有

通过令$x_i^{\prime }=(x_i^{\prime },y_i^{\prime },w_i^{\prime })$，求解$x_i^{\prime }\times H{x}_i=0$有

整理得

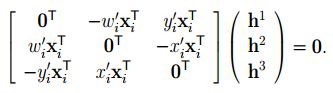
容易观察到左边的矩阵仅有两个是线性独立的，因此可以方程组变为

注意上面都是针对一个点变换的，因此知道，一对匹配点可以构造出两个方程，而我们的单应矩阵自由度是8，因此我们最少需要四对点进行求解。

2.1.1 解法一：最小二乘法 / 高斯消去法（最小配置解情况）

上面方程的右侧是一个9维的向量，其实就是H矩阵九个未知量，根据尺度不变性的理解，这里第一种方法是将尺度不变性理解为九个元素中间的某一个为1，这样就消除了尺度不变性，假定选择最后一个元素为1的话，方程就可以转换为《视觉SLAM十四讲》里面的方程

这是一个线性方程组，如果匹配点的数量多于4对点的话，就是超定方程，采用最小二乘法，如果是4对点的话，就是普通的非齐次线性方程组，采用高斯消去法就可以。
这种方法的确定是，如果所选为1的元素接近0，结果将导致不稳定解，因此更推荐解法二。

2.1.2 解法二：DLT算法

上述方程形式为$Ah=x$，其中矩阵$A$为的秩为8，未知向量$h$的维数为9，如果四对点都是准确点的话，上述方程存在一维的零空间，即存在一个线性解，但是如果匹配点都存在误差的话，通常的做法是在约束$||h||=1$的最小化范数$||Ah||$，即求$||Ah||/||h||$的最小值问题，该问题解为$A^{T}A$的最小特征值的特征矢量，也就是$A$的最小奇异值的奇异矢量，总之其基本DLT算法步骤如下：

在多视图几何中证明了，DLT算法的结果与点的坐标系有关，为了相处坐标系的影响同时使DLT算法关于相似变换不变，提出了归一化的问题，包括图像坐标的平移和尺度缩放，而归一化是再DLT之前必须实施的。其步骤如下：
（1）对点进行平移使其形心位于原点
（2）对点进行缩放使他们到原点的平均距离等于$\sqrt{2}$
（3）对两幅图独立进行上述变换
因此归一化的DLT算法如下：

2.2 基于几何误差的非线性估计

几何误差分好几种情况，包括单图像误差、对称转移误差和重投影误差，如下图

上图的上半图就是对称转移误差，表示为

上图的下半图就是重投影误差，表示为

可以通过DLT获得其初始值，然后通过牛顿法或者列温伯格法进行迭代下降求得最后的值。

基于代数误差的方法会更快，而基于几何误差的方法会根据鲁棒性

3. 基础矩阵求解过程

3.1 基于代数误差的线性估计

基础矩阵的求解方法和单应矩阵就比较相似啦，不过还是有区别的，首先基本矩阵的方程如下：$$x_{i}F{x}_i^{\prime }=0$$与单应矩阵不同的是，对于基本矩阵一对点只能确定一个约束方程，给定n对匹配点就得到如下方程组

下面我换个思路按照点的数量多少对求解方法进行分类：

3.1.1 七个点——最小配置解情形

当矩阵A的秩为7时，其解空间维数为2，因此会有$F_1$和$F_2$两个解，同时$F$又要满足$det(F)$的要求，因此添加一个强迫约束$det(\alpha F_1+(1-\alpha )F_2)=0$，此种情况下矩阵可能有一种或者三种解。

3.1.2 八个点——线性解法

这就是解解空间为1维的线性方程组

3.1.3 n个点——八点法

多视图几何中将n个点的解法成为八点法（明明不是八个点…）

其实就对应着前面的求解单应矩阵的DLT算法，归一化的8点法就是归一化 DLT算法，在此不赘述，需要注意的一点是，单应矩阵不是奇异矩阵，而基础矩阵是奇异矩阵（为什么是奇异矩阵参见MVG总结——基础矩阵、本质矩阵和单应矩阵的自由度分析），因此需要添加一个强迫约束， 即求解在Frobenius范数下最接近$F$的奇异矩阵$F^{\prime }$代替$F$，采用SVD分解，具体解法如下：

2.2 基于几何误差的非线性估计

多视图几何中介绍的除了重投影误差，还介绍了一种对称对极点距离的几何误差，如下：

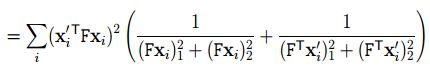
这里顺便插一句，目前state of art的一种过滤动态物体的算法就是基于这种思想完成的DS SLAM

4. 本质矩阵求解过程

4.1 基于代数误差的线性估计

4.1.1 八点法

本质矩阵的八点法求解与基础矩阵是一致的，不同的一点是其强迫约束不同，因为本质矩阵的性质中有一条是其奇异值分解的两个非零奇异值相等，因此再SVD的处理中按照如下方式处理;

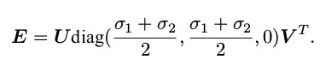
4.1.2 五点法

5点算法的大概思路就是把本征方程展开，再加上本质矩阵的充要条件。化简后得到一个高次多项式方程，该多项式实数解中的一个确定出的本质矩阵是系统的真实本质矩阵，对伪解进行剔除。该方法的具体原理可见论文An efficient solution to the five-point relative pose problem

总结大致如此， 有什么问题欢迎交流～