决策单调性Ⅰ:四边形不等式(bzoj 1563: [NOI2009]诗人小G)
题目描述:
给出n个数字和常数L,你可以任意合并相邻的两个数字a[x]和a[x+1],并得出一个新的数a[x]+a[x+1]+1,一通合并后得到一个有若干个数的序列,这个序列的不协调值为∑|(a[i]-L)^p|,求最小不协调值
例如L=7,初始4个数分别为3 3 1 5,那么肯定是将前两个数合并,后两个数合并得出7 7,这时不协调值一定为0
n<=100000,L<=300000,P<=10
设dp[i]为前i个数的最小不协调度,len[]为第i个数有
复杂度O(n²P),肯定过不去
当P=2时,设sum[]为len[]的前缀和,若k点比j点更优,且j
维护一个下凸包,这样当P=2时,斜率优化复杂度O(n)
斜率优化可见:决策单调性Ⅱ:斜率优化
这就是题目 1010: [HNOI2008]玩具装箱toy 的题解
可这题P不一定等于2,还是过不去
不过以上说明了这个DP可能是有决策单调性的
那么先说:什么是决策单调性?
先提一个词:1D/1D动态规划,指的是状态为O(n),每一个状态决策都需要O(n)遍历前面所有决策才能得出的动态规划,直接求解的复杂度是O(n²),但很多情况下都可以通过一系列手段优化成O(nlogn)或者O(n)(例如平行四边形优化 和斜率优化)
1D/1D动态规划经典模型:
假设j点是当前i点的最优决策,那么决策单调性就是指:
对于所有的x>i,最优决策p(x)一定都大于j
也可这么理解:假设a是dp[x]的最优决策,b是dp[x-1]点的最优决策,a>b,那么对于所有的p>x,从a点转移一定比b点更优,对于所有的p
还可以这么理解:每个决策点能决策的区间一定是连续的一段,并且随着决策点的右移,这个区间也在不断右移
充要条件:
具体证明比较复杂,而且题目不同证明应该也会有不同,这里就略
贴一篇证明https://www.byvoid.com/zhs/blog/noi-2009-poet
一般题目都能看出来,没必要证,等你证完别人都AC了
那么知道了决策单调性,怎么搞?
通过上面蓝色字体,可以这样思考:对于当前决策点,它能影响的区间是哪些?
举个例子假设n=30,一步一步来:
先搞出dp[1],那么所有后续状态dp[x]的目前最优决策一定都是1,决策表如下:
111111111111111111111111111111
然后再算出dp[2],由于决策单调性,决策表一定会变成这样:
111111111122222222222222222
再算出dp[3]:111111111122222233333333333
再算出dp[4]:111111111122222244444444444
再算出dp[5]:111111111122222244555555555
……
那么可以看出,每个决策在决策表中一定会有且只有一个转折点
理论上只要知道这个转折点就可以
具体过程:
用一个栈来维护,里面保存每一个决策的起始位置和终点位置,显然这些位置是首尾相接的
每出现一个新决策,从后往前扫描栈,这个时候有两种情况:
①如果在某个老决策起点处新决策更好,那么把这个老决策直接弹出栈(扔掉),用新决策代替之,就如同上面例子中算出dp[4]之后,决策3被完全抛弃
②如果在某个老决策起点处还是老决策更好,那么转折点必定在这个老决策区间内,二分查找并插入新决策
复杂度分析:每个决策出栈进栈1次,每次二分,所以O(nlogn)
回到这题,看DP式子
这不就是
就用上述方法就ok了
1563: [NOI2009]诗人小G
Time Limit: 100 Sec Memory Limit: 64 MBSubmit: 2736 Solved: 885
[ Submit][ Status][ Discuss]
Description
Input
Output
Sample Input
Sample Output
这题就是上面那个例子,代码里有注释
#include
#include
#include
using namespace std;
#define LL long long
#define Inf 1e18
#define LD long double
int n, L, p, top, st[100005], k[100005], a[100005], sum[100005];
LD dp[100005];
LD Pow(int x, int y)
{
int i;
LD ans = 1;
for(i=1;i<=y;i++)
ans = ans*x;
if(ans<0)
ans = -ans;
return ans;
}
LD Calc(int j, int i)
{
return dp[j]+Pow(sum[i]-sum[j]+i-j-1-L, p);
}
int Find(int x)
{
int l, r, m;
l = 1, r = top;
while(l=k[st[m]])
l = m;
else
r = m-1;
}
return r;
}
int Find_pos(int i, int x)
{
int l, r, m;
l = max(i+1, k[x]+1), r = n+1;
while(li && Calc(i, k[st[top]])Inf)
printf("Too hard to arrange\n--------------------\n");
else
printf("%lld\n--------------------\n", (LL)dp[n]);
}
return 0;
}
/*
1
4 9 2
brysj,
hhrhl.
yqqlm,
gsycl.
*/ 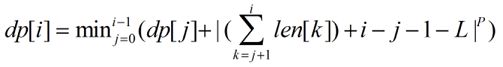
![决策单调性Ⅰ:四边形不等式(bzoj 1563: [NOI2009]诗人小G)_第1张图片](http://img.e-com-net.com/image/info8/5799568be2d2466ea47b89bd1ee78c3f.jpg)