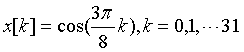信号与系统 Matlab 利用DFT分析离散信号频谱

应用离散傅里叶变换(DFT)，分析离散信号x[k]。根据信号傅里叶变换建立的时域与频域之间的对应关系，可以得到有限长序列的离散傅里叶变换(DFT)与四种确定信号傅里叶变换的之间的关系，实现由DFT分析其频谱。

1. 利用FFT分析信号
   
   的频谱；

   (1) 确定DFT计算的参数；
   (2) 进行理论值与计算值比较，讨论信号频谱分析过程中误差原因及改善方法。
   答：信号下x[k]基频，可以确定基波周期N=16，为显示k=0,1,…31，所以取N=32。

Matlab程序如下：

N=32; k=0:N-1;
x=cos(3*pi*k/8);
X=fft(x);
subplot(2,1,1);
stem(k-N/2,abs(fftshift(X)));
ylabel('Magnitude');   
xlabel('Frequency (rad)');
subplot(2,1,2);
stem(k-N/2,angle(fftshift(X)));
ylabel('Phase');      
xlabel('Frequency (rad)');

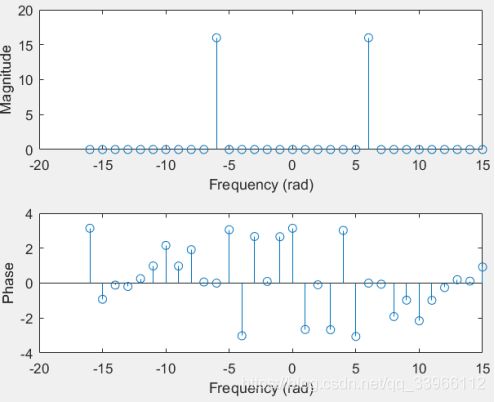
(2)由幅频特性，X[m]在m=6和-6处有值，幅度为16，可以算出基频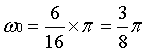，与理论值相符。若选取N不是16或16的整数倍，将发生频谱泄露现象。

2.利用FFT分析信号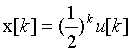的频谱；
(1) 确定DFT计算的参数；
(2) 进行理论值与计算值比较，讨论信号频谱分析过程中误差原因及改善方法。

答：(1)信号无限长，因此需要对其进行截短。该序列单调衰减，当k>=30时，序列已几乎衰减为0，因此只取序列在区间[0，30]上的数值进行分析。
Matlab程序如下：

k=0:30;
k1=-15:15;
x=0.5.^k;
X=fft(x);
subplot(2,1,1);
plot(k-15,abs(fftshift(X)),k1,(1+0.25-cos(k1*pi/15)).^(-0.5),'r');
ylabel('Magnitude');   
xlabel('Frequency (rad)');
subplot(2,1,2);
plot(k-15,angle(fftshift(X)));
ylabel('Phase');      
xlabel('Frequency (rad)');

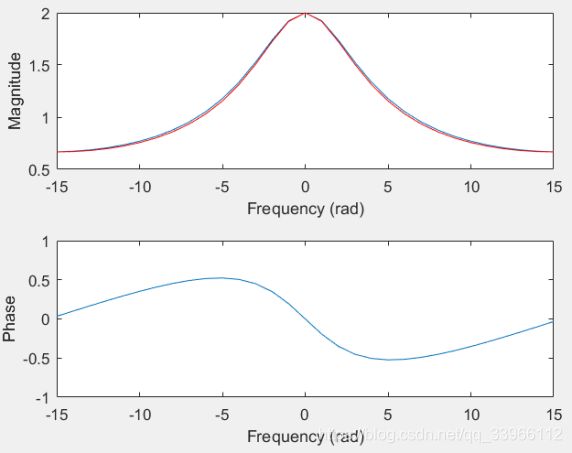
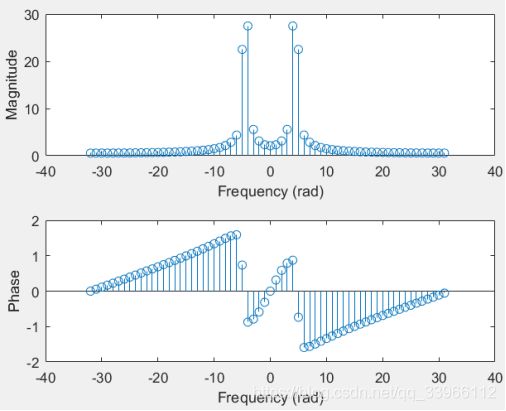
(2)幅频图中蓝线表示计算中，红线表示理论值，可以看出计算值与理论值基本一致，但存在一定误差。因截取序列长度M=30时，该序列几乎衰减为0，且取作FFT点数N>=M，所以计算值与理论值差别不大。若产生较大误差，可能是截取信号长度过短，可以截取较长时间的样点进行分析，或者在截取的离散序列之后补零，得到一个更长的序列，这样可以增加频谱图的更多细节。

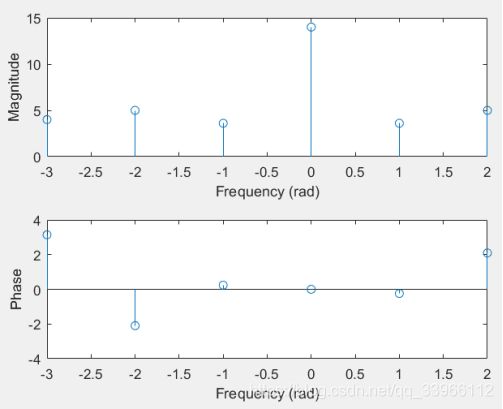
3. 有限长脉冲序列x[k]=[2,3,3,1,0,5;k=0,1,2,3,4,5]，利用FFT分析其频谱，并绘出其幅度谱与相位谱。
   答：原序列长度为6，matlab程序如下：

k=[0,1,2,3,4,5]
x=[2,3,3,1,0,5]
X=fft(x);
subplot(2,1,1);
stem(k-3,abs(fftshift(X)));
ylabel('Magnitude');   
xlabel('Frequency (rad)');
subplot(2,1,2);
stem(k-3,angle(fftshift(X)));
ylabel('Phase');      
xlabel('Frequency (rad)');

4. 某周期序列由3个频率组成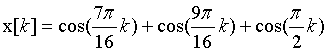： ，利用FFT分析其频谱。如何选取FFT的点数N？此3个频率分别对应FFT计算结果X[m]中的哪些点？若选取的N不合适，FFT计算出的频谱X[m]会出现什么情况？
   答：
   三个余弦信号对应的基波周期分别为N1=32，N2=32，N3=4，最小公共周期N=32,可选取FFT的点数32。matlab程序代码如下：

N=32; k=0:N-1;
x=cos(7*pi*k/16)+cos(9*pi*k/16)+cos(pi*k/2);
X=fft(x);
subplot(2,1,1);
stem(k-N/2,abs(fftshift(X)));
ylabel('Magnitude');   
xlabel('Frequency (rad)');
subplot(2,1,2);
stem(k-N/2,angle(fftshift(X)));
ylabel('Phase');      
xlabel('Frequency (rad)');

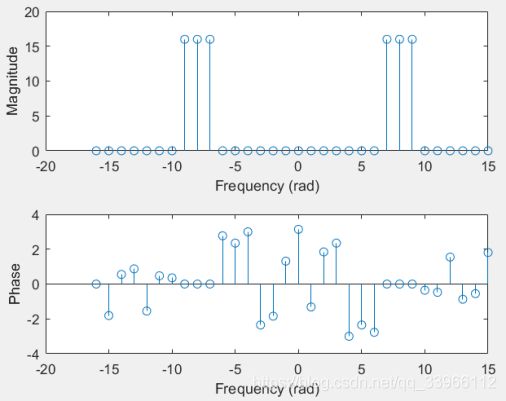
三个基频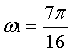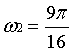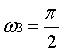，，分别对应频谱图中m=±7，±9，±8这三组点，幅值均为16。若N选取不合适（不是32或32的整数倍），将出现杂频，频谱图X[m]中不能完全分辨出三个频率。

5. 某离散序列由3个频率组成:
   利用FFT分析其频谱。
   (1) 对x[k]做64点FFT，绘出信号频谱，能分辨出其中的两个频率吗？
   (2) 对x[k]补零到256点后计算FFT，能分辨出其中的两个频率吗？
   (3) 选用非矩形窗计算FFT，能够分辨出其中的两个频率吗？
   (4) 若不能够很好地分辨出其中的两个频谱，应采取哪些措施？
   答：(1)

N=64; k=0:N-1;
x=cos(2*pi*k/15)+0.75*cos(2.3*pi*k/15);
X=fft(x);
subplot(2,1,1);
stem(k-N/2,abs(fftshift(X)));
ylabel('Magnitude');   
xlabel('Frequency (rad)');
subplot(2,1,2);
stem(k-N/2,angle(fftshift(X)));
ylabel('Phase');      
xlabel('Frequency (rad)');

对x[k]作64点FFT，出现杂频，不能分辨出两个频率。

(2)对x[k]补零至256点后计算FFT，绘制出频谱图如下:

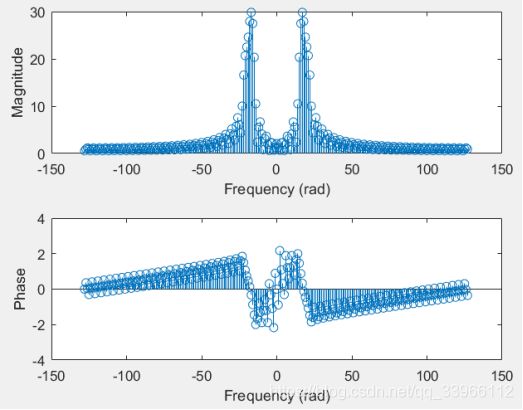
对时域序列补零至256点后，增加了频谱图中更多的细节，但是没有提高频率分辨率，不能分辨出两个频率。

(3)若选用非矩形窗(主要有汉宁窗、哈明窗、布拉克曼窗和凯塞窗)计算FFT，可以分辨出其中两个频率。

(4)可以提高序列样点数，以下是对x[k]作300点FFT得到得频谱图：

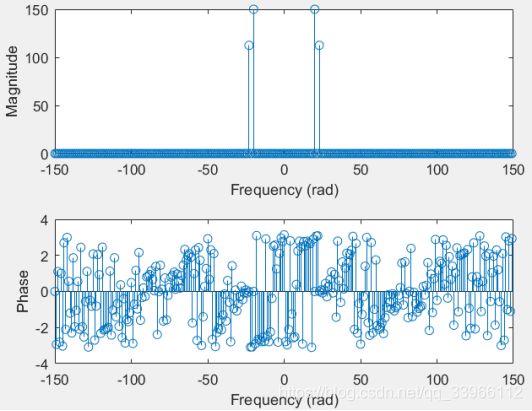
可以分辨出两个频率。

6. 已知序列
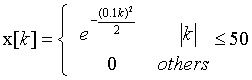
   利用FFT分析下列信号的幅频特性，频率范围为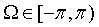，N=500点。
   (1)y[k]=x[2k]
   (2) g[k]=x[4k]
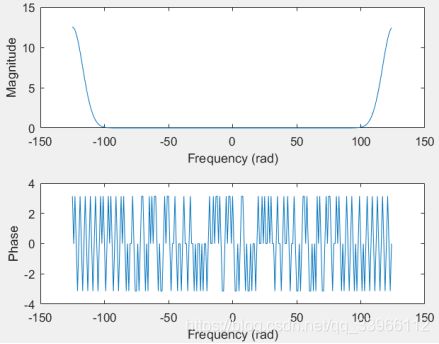
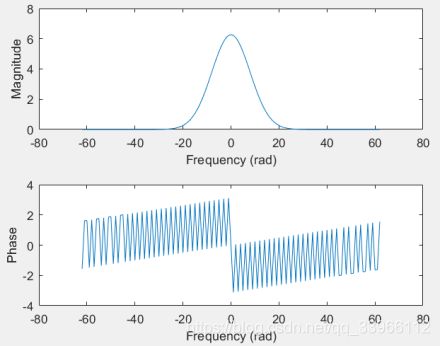
   (3) 若将上述x[k]乘以cos(pk/2) ，重做(1)和(2)。
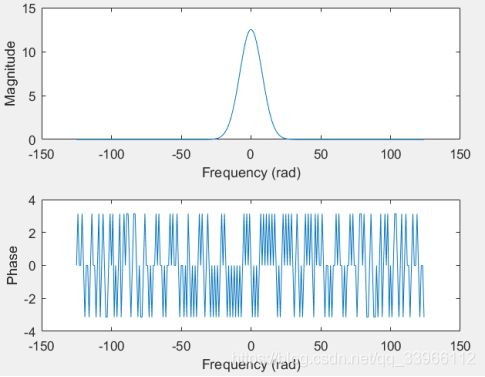
   答：(1)

k=-125:124;
y=(abs(2*k)<=50).*exp(-(0.1*2*k).^2/2);
Y=fft(y);
subplot(2,1,1);
plot(k,abs(fftshift(Y)));
ylabel('Magnitude');   
xlabel('Frequency (rad)');
subplot(2,1,2);
plot(k,angle(fftshift(Y)));
ylabel('Phase');      
xlabel('Frequency (rad)');

(2)

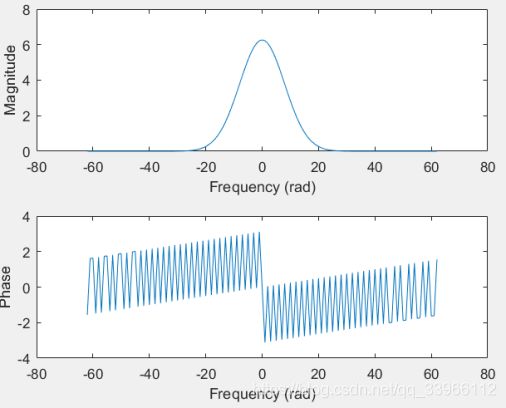
k=-62:62;
g=(abs(4*k)<=50).*exp(-(0.1*4*k).^2/2);
G=fft(g);
subplot(2,1,1);
plot(k,abs(fftshift(G)));
ylabel('Magnitude');   
xlabel('Frequency (rad)');
subplot(2,1,2);
plot(k,angle(fftshift(G)));
ylabel('Phase');      
xlabel('Frequency (rad)');

(3)上述代码中y[k],g[k]用以下表达式替换：

y=(abs(2*k)<=50).*exp(-(0.1*2*k).^2/2).*cos(pi*2*k/2)
g=(abs(4*k)<=50).*exp(-(0.1*4*k).^2/2).*cos(pi*4*k/2)

Y[m]:

G[m]: