2020HDU多校第六场--A Very Easy Graph Problem（最小生成树+DFS序 建立线段树 or 树状数组）

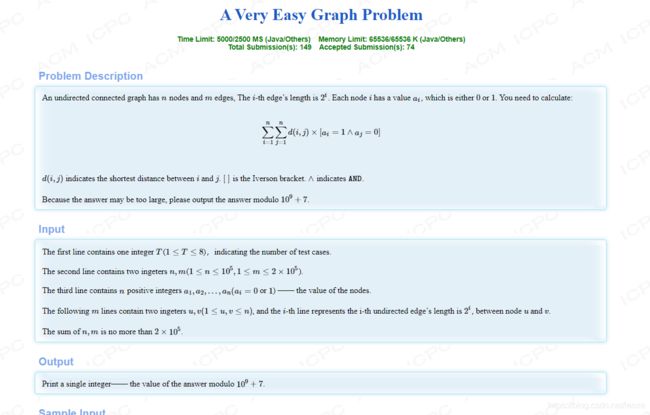
题意：给出一个连通图，对于任意两个标记不同（0或1）的点，找出它们之间的最短路径，然后求和
暴力floyd???
大体思路是求一个最小生成树用到了那些边，同时任意选取一个点进行$DFS$序，记录下每个点的$in$数组和$out$数组，最后遍历用到的每条边，求出他左右0点和1点的个数，对每条边的贡献进行累加求和
-------------------------------
我用的树状数组，书写简单

首先题目说第$i$条边的权值就是$2^i$，那么根据等比数列求和就能得出第$i$条边的权值是大于前面$i-1$条边的权值之和的，所以对于任意两点，当他们第一次连通的时候（处于同一个集合内），那此时它们之间的距离就是 最短距离
所以我们先利用一个类似于$kruskal$的思想进行并查集求出最终图的每条边，（题目已经说明了边的权值是递增的，所以直接并查集就好了
似乎并不需要记录度数…我多此一举了

for(int i = 1; i <= m; ++ i) {
        int u, v; scanf("%d %d", &u, &v);
        // 建立最小生成树
        if(seek(u) != seek(v)) {
            // 记录边
            vec[++ Num] = MP(u, v);
            ++ deg[u];
            ++ deg[v];
            dad[seek(u)] = seek(v);
            LL w = qpow(2, i, mod);
            cup[Num] = w;
            // 储存每个点所相连的点
            G[u].emplace_back(v);
            G[v].emplace_back(u);
        }
    }

之后对于得到的最小生成树的每条边，我们进行一次$DFS$求出$DFS$序，并用这个建立一颗线段树（树状数组也可），用$in$时间戳代表每个点的位置，并把这个点的权值设置为它的标记(0 $or$ 1)

// DFS序记录时间戳
void build(int rt, int fa) {
    in[rt] = ++ tot;
    for(int i = 0; i < G[rt].size(); ++ i) {
        int v = G[rt][i];
        if(v != fa) {
            build(v, rt);
        }
    }
    out[rt] = ++ tot;
}

// 建树
void updata(int x) {
    while(x <= n * 2) {
        Trie[x] ++;
        x += lowbit(x);
    }
}
// 初始化
for(int i = 1; i <= n; ++ i) {
    if(id[i] == 1) {
        updata(in[i]);
    }
}

之后我们开始遍历生成树的每一条边，对于一条边形如($u$,$v$ = $w$)
由于对于一棵树而言。任意两点之间的路径是固定的，所以我们需要求出$u$及$u$前面0和1的数目，$v$及$v$后面0和1的数目，这条边的贡献的次数$cnt$就是前面0乘于后面1加上前面1乘于后面0，贡献的价值就是边权乘于次数$cnt$

至于两边0和1的个数怎么求，就是我们建立线段树的意义所在了，方便起见，我们可以用一次$swap$来把$u$设置为时间戳小的点，$v$设置成时间戳大的点，这样以来，我们只需要求出$v$点的入时间戳和出时间戳这个区间内1的个数，那我们就可以求出这个区间内0的个数了（区间大小减去1的个数），同时我们记录下总的1的个数和0的个数，就直接求出外面的0的个数和1的个数了
详细过程看下面
$vec$数组内储存的最小生成树的每条边

// 累积贡献
for(int i = 1; i <= n - 1; ++ i) {
        int u = vec[i].fi, v = vec[i].se;
        // 方便起见  把u换到左边（时间戳小的地方）
        if(in[u] > in[v]) {
            swap(u, v);
        } 
        // 区间内所有的数的个数
        int cnt = (out[v] - in[v] + 1) / 2;
        // 区间内1的个数
        int right1 = query(out[v]) - query(in[v] - 1);
        // 区间内0的个数
        int right0 = cnt - right1;
        //  区间外面0和1的个数  就是直接总数减区间内的
        int left0 = nn0 - right0;
        int left1 = nn1 - right1;
        // 左0右1的贡献
        res += (LL)(left0 * right1) % mod * cup[i] % mod;
        res %= mod;
        // 左1右0的贡献
        res += (LL)(left1 * right0) % mod * cup[i] % mod;
        res %= mod;
    }

全部代码就是如下（修改了一波代码风格之后贴上来的，，比赛时写的有点丑，全是注释符号啥的
注意似乎并不需要从度数为1的点开始DFS序，我多此一举了，直接任意选取就可以了

#include 
using namespace std;
typedef long long  LL;
typedef pair<int, int>  pii;
#define de(x)   cout << "-----debug----  " << #x << " == " << x << endl;
#define rep(i, a, n)    for(int i = a; i <= n; ++ i)
#define per(i, n, a)    for(int i = n; i >= a; -- i)
#define ms(arr, x)      memset(arr, x, sizeof(arr))
#define MP  make_pair
#define fi  first
#define se  second
const LL mod = 1e9 + 7;
const int inf = 0x3f3f3f3f;
inline int lowbit(int x) { return x & (-x);}
inline LL qpow(LL x, LL n, LL m) { 
    LL res = 1;
    while(n) {
        if(n & 1) {
            res = res * x % m;
        }
        n >>= 1;
        x = x * x % m;
    }
    return res % m;
}
const int maxn = 1e5 + 7;
const int maxm = 2e6 + 7;
vector<int> G[maxn];
pii vec[maxn];
LL cup[maxn], res;
int dad[maxn], id[maxn], deg[maxn];
int seek(int x) { return x == dad[x] ? x : dad[x] = seek(dad[x]);}
int n, m, in[maxn], out[maxn], tot, Num = 0;
int Trie[maxn << 1];
// DFS序记录时间戳
void build(int rt, int fa) {
    in[rt] = ++ tot;
    for(int i = 0; i < G[rt].size(); ++ i) {
        int v = G[rt][i];
        if(v != fa) {
            build(v, rt);
        }
    }
    out[rt] = ++ tot;
}
void updata(int x) {
    while(x <= n * 2) {
        Trie[x] ++;
        x += lowbit(x);
    }
}
int query(int x) {
    int sum = 0;
    while(x >= 1) {
        sum += Trie[x];
        x -= lowbit(x);
    }
    return sum;
}
void Solve(int& kase) {
    ms(Trie, 0);
    Num = 0;
    // 总共0的个数  1的个数
    int nn0 = 0, nn1 = 0;

    scanf("%d %d", &n, &m);
    for(int i = 1; i <= n; ++ i) {
        deg[i] = 0;
        dad[i] = i;
        G[i].clear();
        scanf("%d", &id[i]);
        nn0 += (id[i] == 0);
        nn1 += (id[i] == 1);
    }
    for(int i = 1; i <= m; ++ i) {
        int u, v; scanf("%d %d", &u, &v);
        // 建立最小生成树
        if(seek(u) != seek(v)) {
            // 记录边
            vec[++ Num] = MP(u, v);
            ++ deg[u];
            ++ deg[v];
            dad[seek(u)] = seek(v);
            LL w = qpow(2, i, mod);
            cup[Num] = w;
            G[u].emplace_back(v);
            G[v].emplace_back(u);
        }
    }
    res = 0;
    tot = 0;
    int root;
    // DFS序
    for(int i = 1; i <= n; ++ i) {
        if(deg[i] == 1) {
            root = i;
            build(i, 0);
            break;
        }
    }
    // 初始化
    for(int i = 1; i <= n; ++ i) {
        if(id[i] == 1) {
            updata(in[i]);
        }
    }
    for(int i = 1; i <= n - 1; ++ i) {
        int u = vec[i].fi, v = vec[i].se;
        // 方便起见  把u换到左边（时间戳小的地方）
        if(in[u] > in[v]) {
            swap(u, v);
        } 
        // 区间内所有的数的个数
        int cnt = (out[v] - in[v] + 1) / 2;
        // 区间内1的个数
        int right1 = query(out[v]) - query(in[v] - 1);
        // 区间内0的个数
        int right0 = cnt - right1;
        //  区间外面0和1的个数  就是直接总数减区间内的
        int left0 = nn0 - right0;
        int left1 = nn1 - right1;
        // 左0右1的贡献
        res += (LL)(left0 * right1) % mod * cup[i] % mod;
        res %= mod;
        // 左1右0的贡献
        res += (LL)(left1 * right0) % mod * cup[i] % mod;
        res %= mod;
    }
    printf("%lld\n", res % mod);
}
int main () {

    int Test = 1, kase = 0;
    scanf("%d", &Test);
    while(Test --) {
        ++ kase;
        Solve(kase);
    }
    #ifdef iyua
        system("pause");
    #endif
    return 0;
}