2016湖南省省赛-K:盖房子(单调栈)
链接:https://ac.nowcoder.com/acm/contest/1112/K
时间限制:C/C++ 1秒,其他语言2秒
空间限制:C/C++ 32768K,其他语言65536K
Special Judge, 64bit IO Format: %lld
题目描述
Bobo 在 ICPCCamp 买了一块 n × m n×m n×m 的土地,其中有些格子是障碍。
他想选择两个矩形区域,建造两座房子。
很明显,用于盖房子的区域不能包含障碍。同时,两个区域不能相交(但是可以相邻)。
Bobo 想知道所有可能不同方案的数量除以 ( 1 0 9 + 7 ) (10^9 + 7) (109+7) 的余数。
输入描述:
输入包含不超过 10 组数据。
每组数据的第一行包含两个整数 n , m ( 1 ≤ n , m ≤ 1 0 3 ) . n, m (1 \leq n, m \leq 10^3). n,m(1≤n,m≤103).
接下来 n 行中的第 i 行包含一个长度为 m 的字符串 s i s_i si 。
s i s_i si 的第 j 位是 0 则表示第 i 行第 j 列的格子是空地,是 1 则表示该格子是障碍。
输出描述:
对于每组数据,输出一个整数表示所求的值。
示例1
输入
2 2
00
01
输出
5
示例2
输入
3 4
1000
0001
0100
输出
160
思路: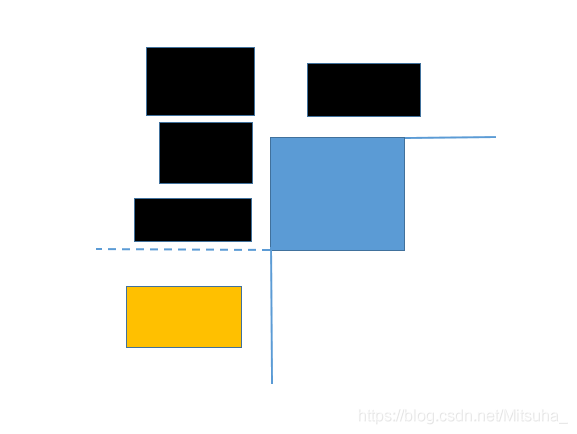
首先利用单调栈求出
A [ i ] [ j ] ( 右 下 角 位 于 ( i , j ) 的 矩 形 个 数 ) A[i][j](右下角位于(i,j)的矩形个数) A[i][j](右下角位于(i,j)的矩形个数), B [ i ] [ j ] ( 右 上 角 位 于 ( i , j ) 的 矩 形 个 数 ) B[i][j](右上角位于(i,j)的矩形个数) B[i][j](右上角位于(i,j)的矩形个数), C [ i ] [ j ] ( 左 下 角 位 于 ( i , j ) 的 矩 形 个 数 ) C[i][j](左下角位于(i,j)的矩形个数) C[i][j](左下角位于(i,j)的矩形个数), D [ i ] [ j ] ( 左 上 角 位 于 ( i , j ) 的 矩 形 个 数 ) D[i][j](左上角位于(i,j)的矩形个数) D[i][j](左上角位于(i,j)的矩形个数)。
我们枚举所有矩形的左上角(如图中蓝色矩形),即每个 D [ i ] [ j ] D[i][j] D[i][j]。
那么位于图中黑色和黄色矩阵所处位置的矩形一定不会与左上角在 ( i , j ) (i,j) (i,j)的矩形相交,因为该区域的矩形的右下角都是在 ( i , j ) (i,j) (i,j)覆盖范围之外的。
那么对于左上角在 ( i , j ) (i,j) (i,j)的 D [ i ] [ j ] D[i][j] D[i][j]个矩形,其对答案的贡献为 D [ i ] [ j ] ∗ ∑ x < i ∣ ∣ y < j A [ x ] [ y ] D[i][j]*\sum_{x
但是这样会产生重复,如图中的黄色和蓝色矩形,他们之间的贡献会被算2次,这时需要去重。
枚举每个左下角在 ( i , j ) (i,j) (i,j)的矩形,即 C [ i ] [ j ] C[i][j] C[i][j],其所产生的重复为 C [ i ] [ j ] ∗ ∑ x > i & & y < j B [ x ] [ y ] C[i][j]*\sum_{x>i\&\&y
#include