Codeforces Global Round 8 （A,B,C,D,F）题解

一段时间没训练了，状态就是下滑了。。。
一场很可惜的cf。。。

比赛链接

								A  C+=

大意：

最初给你两个数a,b,和一个数n；
你可以进行任意操作，每次操作包含两种情况 a+=b，b+=a。
问你你最少经过几次操做可以a,b中出现一个严格大于n的数。

思路：
首先可以发现a,b的值可以互换而没有影响，然后我就让b为a,b中最大的那个数。
然后再发现，你如果只进行一次操作，会出现两种情况
1 (a,a+b);
2 (b,a+b);
很明显操作2更优，然后就是每次操作都选操作二就行了，复杂度大约是log级别的。
代码：

#include
using namespace std;
const int N=1e3+15;
typedef long long ll;
int main()
{
    ll t,b,a,n;
    cin>>t;
    while(t--)
    {
        ll cnt=0;
        cin>>a>>b>>n;
        if(a>b)
            swap(a,b);
        if(a>n)
        {
            cout<<"0"<<endl;
            continue;
        }
        if(a+b>n)
        {
            //cnt++;
            cout<<"1"<<endl;
            continue;
        }
        if(a+2*b>n)
        {
            //cnt++;
            cout<<"2"<<endl;
            continue;
        }
        while(1)
        {
            cnt+=2;
            ll c=a+2*b;
            a=a+b;
            b=c;
            if(a+b>n)
            {
                //cnt++;
                cout<<(1+cnt)<<endl;
                break;//continue;
            }
            if(a+2*b>n)
            {
                //cnt++;
                cout<<(2+cnt)<<endl;
                break;//continue;
            }
        }
    }
    return 0;
}

					B. Codeforces Subsequences

状态太差在这里卡了好久，因为预处理范围弄小了，好像上一场也出现这种情况了，
以后写题要认真一些，不能只是抱着先验证思路的状态，而是刚开始就认真对待它。

题意：
给你一个k，你要找到一个字符串，其中有最少k个子序列是codeforces。

思路：
codeforces 有1个
codeforcess 有2个
codeforceess 有4个
codeforcceess 有8个
…
ccooddeeffoorrcceesss有(512*3=1536)个。
…
规律就是这样。

代码：

#include
using namespace std;
const int N=1e2+15;
typedef long long ll;
ll f[N][N];
int main()
{
    ll t,b,a,n,k;
    for(int i=1;i<=100;i++)
    {
        f[i][0]=1;
        for(int j=1;j<=100;j++)
        {
            f[i][j]=f[i][j-1]*i;
        }
    }
    char str[100];
    str[1]='c';
    str[2]='o';
    str[3]='d';
    str[4]='e';
    str[5]='f';
    str[6]='o';
    str[7]='r';
    str[8]='c';
    str[9]='e';
    str[10]='s';
    cin>>k;
    if(k==1)
    {
        cout<<"codeforces"<<endl;   return 0;
    }
    if(k<=2)
    {
        cout<<"codeforcess"<<endl;   return 0;
    }
    if(k<=4)
    {
        cout<<"codeforceess"<<endl;   return 0;
    }
    for(int i=1;i<=100;i++)
    {
        if(f[i][10]>k)
        {
            for(int j=10;j>=0;j--)
            {
                ll op=f[i-1][j]*f[i][10-j];
                if(op>=k)
                {
                    for(int l=1;l<=j;l++)
                    {
                        for(int r=1;r<=i-1;r++)
                            cout<<str[l];
                    }
                    for(int l=j+1;l<=10;l++)
                    {
                        for(int r=1;r<=i;r++)
                            cout<<str[l];
                    }
                    cout<<endl;
                    return 0;
                }
            }
        }
    }
    return 0;
}

						C. Even Picture

	C也是一个很烦的题，这场真的好多我不喜欢的题呀。。。。

题意：你有一个包含很多个格子的图，你可以把一些格子涂成黑色。
但是你在涂色的时候有一些要求
1 所有灰色格子都是任意可达的，即灰色格子都是联通的。
2 每个灰色格子的邻居中，灰色格子的数量是偶数。
然后给你一个数n，n的意义是上下左右都是灰色格子的格子数。
让你把这个图构造出来
思路：
首先手玩n=1,n=2,n=3 。请看图

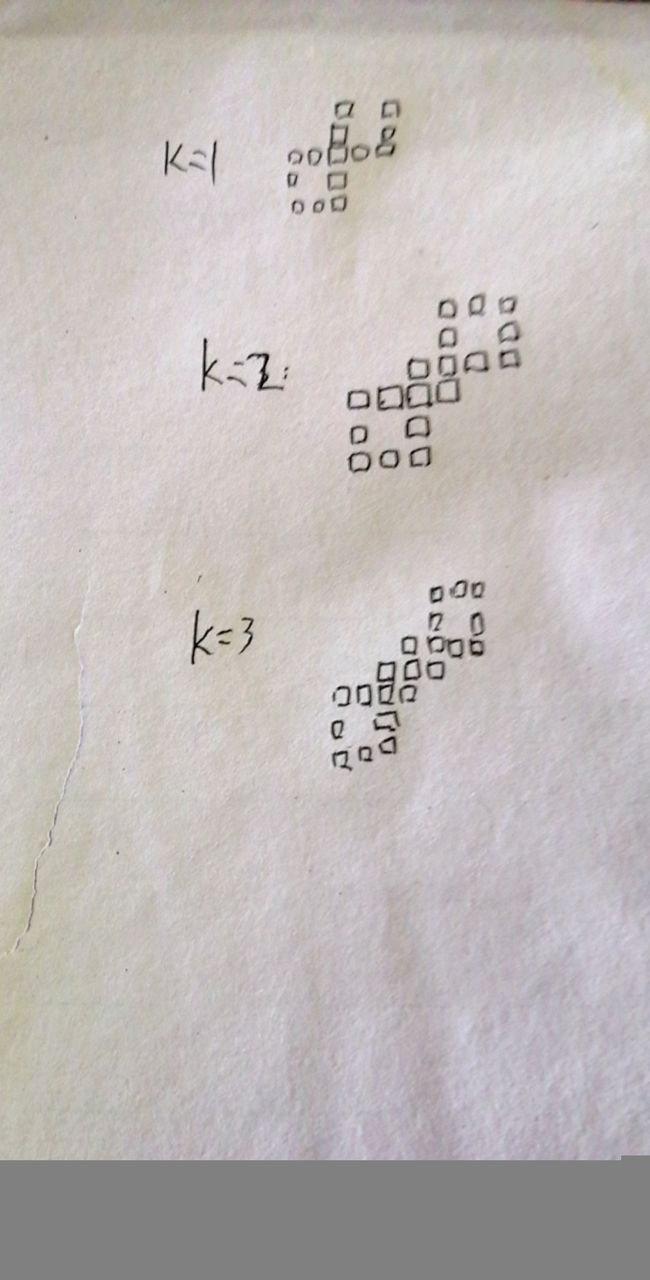
然后规律就是这样，不过我实现了很久，因为现在不是很喜欢写代码。。。(感觉有必要练一练模拟了)。。。
代码：

#include
using namespace std;
const int N=1e6+15;
typedef long long ll;
ll p[N],vis[N],a[N];
int main()
{
    ll k;
    cin>>k;
    ll op=k*3+2+10;
    cout<<op<<endl;
    cout<<"0 0"<<endl;
    cout<<"1 0"<<endl;
    cout<<"2 0"<<endl;
    cout<<"0 1"<<endl;
    cout<<"2 1"<<endl;
    cout<<"0 2"<<endl;
    cout<<(k+3)<<" "<<(k+1)<<endl;
    cout<<(k+3)<<" "<<(k+2)<<endl;
    cout<<(k+3)<<" "<<(k+3)<<endl;
 
    cout<<(k+2)<<" "<<(k+3)<<endl;
    cout<<(k+1)<<" "<<(k+3)<<endl;
    cout<<(k+1)<<" "<<(k+2)<<endl;
 
    for(int i=2;i<=k+1;i++)
    {
        cout<<(i-1)<<" "<<(i)<<endl;
        cout<<(i)<<" "<<(i)<<endl;
        cout<<(i+1)<<" "<<(i)<<endl;
    }
 
    return 0;
}

					D. AND, OR and square sum

题意：
给你一个数n，和 n个数 。
你可以进行任意次操作。
每次操作就是找两个数x,y; 让x = x | y , y = y & x ;
问你 你选择最好的策略来操作，得到的最大的他们这些数的平方之和是多少。

思路：
首先想到
如果x=1,y=1,那么经过一次操作后无影响。
如果x=0,y=0,那么经过一次操作后无影响。
如果x=1,y=0,那么经过一次操作后无影响。
如果x=0,y=1,那么经过一次操作后x=变成1,y变成0。
然后发现这对于所有的二进制对应位数都一样。
然后就想到这代表可以在二进制情况下任意交换0和1。
然后记录二进制下每一位上1的个数，贪心的一直构造目前所能构造的最大数就可以了。

代码：

#include
using namespace std;
const int N=1e6+15;
typedef long long ll;
ll p[N],vis[N],a[N];
int main()
{
    ll n;
    p[0]=1;
    for(int i=1;i<=25;i++)
    {
        p[i]=p[i-1]*2;
    }
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
    }
    for(int i=1;i<=n;i++)
    {
        ll x=a[i];
        for(int j=0;j<=23;j++)
        {
            if(x&p[j])
                vis[j]++;
        }
    }
    ll ans=0;
    for(int i=1;i<=n;i++)
    {
        ll x=0;
        for(int j=0;j<=23;j++)
        {
            if(vis[j]>0)
            {
                vis[j]--;
                x=x|p[j];
            }
        }
        ans+=x*x;
    }
    cout<<ans<<endl;
    return 0;
}

						F. Lamps on a Circle

写的第一道交互题。	
思路很好想，不过格式出了点问题。
以后应该不再烦交互题了。

题意：
刚开始有n盏灯围成一个环，你和imp轮流玩游戏，回合制操作，你先手。
每次轮到你操作，你可以选择结束游戏，或者继续玩下去。
继续玩下去的话你就先选择一个数k,然后选择k盏灯把他们点亮，对于本来就亮着的无影响。
然后imp操作，他选择一个数x，然后从x开始，顺时针关掉k盏灯，对于本来就关着的也无影响。
你想让开着的灯的数量最大，imp想让关着的灯的数量最大。
imp很聪明，你也是。
然后你经过若干次轮回后会得到最大的灯可以亮着的数量。然后结束。

思路：
先看这些
n=5,10100 ,可以亮两盏
n=7，1010100，亮三盏。
n=13,1110111011100，亮9盏。
n=15,111011101110110，亮8盏。
然后就很显然，最终情况都是这样的，你找到一个数k，它亮k-1盏，关1盏，亮k-1盏，关1盏。。。一直到结尾特判。
然后怎么寻找k呢？
你如果选择k，会得到的最大数量是(k-1)*n/k - (k-1)
然后你如果选择k+1,会得到的最大数量是(k)*n/(k+1)-k;
比较选择k可以获得的最大数量和选择k+1获得的最大数量。
就是比较(k-1)*n/k - (k-1) 和 (k)*n/(k+1)-k 的大小。
用减法，来比较，化简后得到 下面式子：
k · (k+1) > n;
找到第一个k 就行，因为k再变大的话数量也会出现衰减。
然后代码写起来也还行，不过我那时以为imp会一直做最优决策，但发现并不是，这就是交互提吧，需要加个特判。

#include
using namespace std;
const int N=1e3+15;
typedef long long ll;
int main()
{
    ll n,d;
    cin>>n;
    if(n<=3){
        cout<<"0"<<endl;
        return 0;
    }
    for(d=1;;d++)
        if(d*(d+1)>n)
            break;
    ll op=d+1,x=1;
    for(ll i=1;;i++){
        if(op>=n)
            break;
        cout<<d<<" ";
        for(int j=1;j<=d-1;j++){
            if(x+j-1<=n)
                cout<<(x+j-1)<<" ";
            else
                cout<<(x+j-1-n)<<" ";
        }
        ll lx=x+d-2;
        if(lx>op)
            cout<<(x-1)<<endl;
        else
            cout<<op<<endl;
        op++;
        if(op%d==0)
            op++;
        cin>>x;
    }
    cout<<"0"<<endl;
    return 0;
}