无监督学习 | 层次聚类 之凝聚聚类原理及Sklearn实现

相关文章：

机器学习 | 目录

机器学习 | 聚类评估指标

机器学习 | 距离计算

无监督学习 | KMeans 与 KMeans++ 原理

无监督学习 | DBSCAN 原理及Sklearn实现

无监督学习 | GMM 高斯混合聚类原理及Sklearn实现

1. 层次聚类

层次聚类（hierarchical clustering）试图在不同层次对数据集进行划分，从而形成树形的聚类结构。数据集的划分可采用“自底向上”的聚合策略，也可采用“自顶向下”的分拆策略。^[1]

因此其优点是可以层次化聚类，将聚类结构视觉化；而缺点是计算量大，我们将在后面提到这一点。

1.1 凝聚聚类

凝聚聚类（Agglomerative Clustering）是一种采用自底向上聚类策略的层次聚类算法。它先将数据集中的每个样本看作一个初始聚类簇，然后在算法运行的每一步中找出距离最近的两个聚类簇进行合并。该过程不断重复，直到达到预设的聚类簇个数。这里的关键是如何计算聚类簇之间的距离。实际上，每个簇是一个样本集合，因此，只需要采用关于集合的某种距离即可。例如，给定聚类簇 $C_i$ 与 $C_j$，可通过下面的式子来计算距离：

$$最小距离：d_{\min }\left(C_i,C_j\right)=\underset{\mathbf{x}\in C_i,\mathbf{z}\in C_j}{\min }\mathrm{dist}(\mathbf{x},\mathbf{z})\text{\hspace{1em}(1)}$$

$$最大距离：d_{\max }\left(C_i,C_j\right)=\underset{\mathbf{x}\in C_i,\mathbf{z}\in C_j}{\max }\mathrm{dist}(\mathbf{x},\mathbf{z})\text{\hspace{1em}(2)}$$

$$平均距离：d_{\mathrm{avg}}\left(C_i,C_j\right)=\frac{1}{\left|C_i\right|\left|C_j\right|}\sum _{\mathbf{x}\in C_i}\sum _{\mathbf{z}\in C_j}\mathrm{dist}(\mathbf{x},\mathbf{z})\text{\hspace{1em}(3)}$$

显然，最小距离由两个簇的最近样本决定，最大距离由两个簇的最远样本决定，而平均距离则由两个簇的所有样本共同决定。

此外，也可以使用离差平方和 ESS（Error Sum of Squares）来进行聚类，通过最小化聚类前后的离方平方和之差 $\Delta (C_i,C_j)$，来寻找最近的簇。^[2]

$$离差平方和：ESS=\sum _{i=1}^n{x}_i^2-\frac{1}{n}(\sum _{i=1}^n{x}_i{)}^2\text{\hspace{1em}(4)}$$

$$\Delta (C_i,C_j)=ESS(C_i\cup C_j)-ESS(C_i)-ESS(C_j)\text{\hspace{1em}(5)}$$

---

当聚类簇距离由 $d_{min}$、$d_{max}$、$d_{avg}$ 或 $\Delta (C_i,C_j)$ 计算时，凝聚聚类算法被相应地称为单链接（single-linkage）、全链接（complete-linkage）)、均链接（average-linkage）和 Ward-linkage 算法。

凝聚聚类算法描述如下图所示：

• 在第 1-9 行，算法先对仅包含一个样本的初始聚类簇和相应的距离矩阵进行初始化；

• 在第 11-23 行，凝聚算法不断合并距离最近的聚类簇，并对合并得到的聚类簇的距离矩阵进行更新；

上述过程不断重复，直到达到预设的聚类簇数。

图1 凝聚聚类算法

1.2 层次图

下面以单链接为例子，介绍层次聚类的层次图（系统图，dendrogram）。假设我们有以下八个点，使用单链接聚为 3 个类。

首先将每个点设为一个单独的簇类，因此此时有 8 个簇，大于预期 3 个簇，故需要继续进行聚类。

图2 初始化聚类簇

因此我们重复算法 11-23 行 3 次，每次将距离最近的两个样本聚为同一簇，对应右图的层次图。此时仍剩下 5 个簇，因此需要继续进行聚类。

图3 5个聚类簇

可以看到，此时样本 7 与簇 {6,8} 的距离（$dis{t}_{min}=dist(6,7)$）最近，因此可以将他们聚为一簇，如下图所示：

图4 4个聚类簇

同理，继续进行聚类，考虑各个簇之间的距离，可以看出，样本 3 与簇 {4,5} 的距离（$dis{t}_{m}in=dist(3,4)$）最近，因此有：

图5 3个聚类簇

此时已经达到了我们所要求的聚类簇数，故算法停止，对应的层次图如右方所示。

---

1.3 不同凝聚算法比较

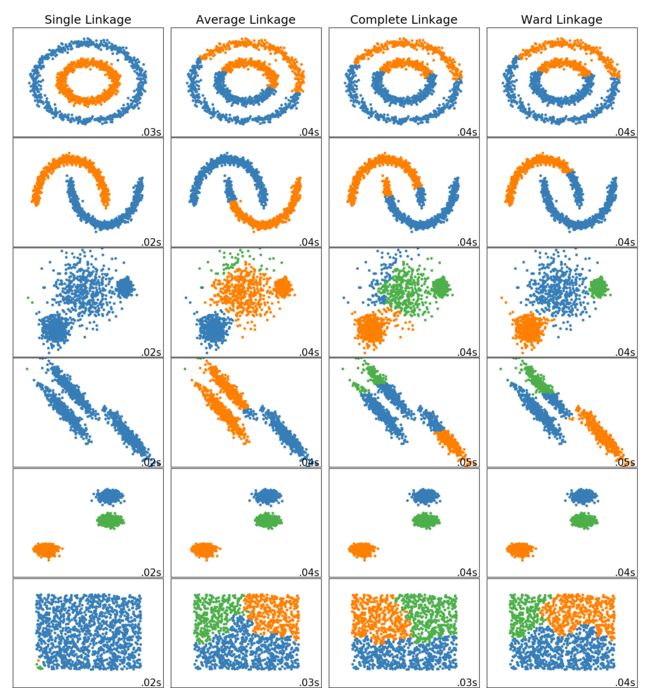
通过下面图片，我们可以看到各类凝聚算法在不同类型数据上的聚类效果，

需要注意的是，由于单链接和全链接只考虑簇中两个代表性的点，故受噪声和异常点影响大；而单链接容易出现一个簇囊括大多数样本（左下方图），而全链接则比单链接更紧凑些。

图6 不同凝聚算法比较

2. Sklearn 实现

sklearn.cluster.AgglomerativeClustering(n_clusters=2, affinity=‘euclidean’, memory=None, connectivity=None, compute_full_tree=‘auto’, linkage=‘ward’, distance_threshold=None)

n_clusters：聚类簇数

affinity： string or callable, default: “euclidean” 【距离计算参数】

Metric used to compute the linkage. Can be “euclidean”, “l1”, “l2”, “manhattan”, “cosine”, or “precomputed”. If linkage is “ward”, only “euclidean” is accepted. If “precomputed”, a distance matrix (instead of a similarity matrix) is needed as input for the fit method.

linkage： {“ward”, “complete”, “average”, “single”}, optional (default=”ward”)

Which linkage criterion to use. The linkage criterion determines which distance to use between sets of observation. The algorithm will merge the pairs of cluster that minimize this criterion.

• ward minimizes the variance of the clusters being merged.

• average uses the average of the distances of each observation of the two sets.

• complete or maximum linkage uses the maximum distances between all observations of the two sets.

• single uses the minimum of the distances between all observations of the two sets.

2.1 层次图可视化

由于 Sklearn 中并不支持可视化层次图，因此我们使用 Scipy：

from scipy.cluster.hierarchy import dendrogram, ward, single
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt

X = load_iris().data[:10]

linkage_matrix = ward(X)

dendrogram(linkage_matrix)

plt.show

图7 层次树可视化

参考文献

[1] 周志华. 机器学习[M]. 北京: 清华大学出版社, 2016: 214.

[2] Ward J H , Jr. Hierarchical Grouping to Optimize an Objective Function[J]. Journal of the American Statistical Association, 1963, 58(301):236-244.