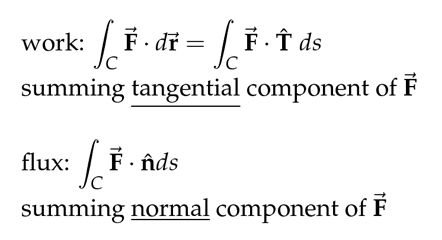Multivariable Calculus 总结（第二部分）

Line Integrals

三种基本的曲线积分种类

line integrals with respect to arc length

求曲线长度的积分一目了然： L=∫bads ，其中的 ds=(dx)2+(dy)2−−−−−−−−−−−√=(dxdt)2+(dydt)2−−−−−−−−−−−−√dt . 根据这个我们有了对弧长的线积分，它的基本形式如下：

∫Cf(x,y)ds

从上面的曲线积分中可以看出，它的积分是一重的，而 differential 却有2个，因此我们一定需要参数化方程，从而去掉一个变量，在上面求曲线长度的积分中，变量 x,y 被参数化成了一个变量 t 。下图是我从 Paul’s Online Math Notes 截下来几种基本曲线的参数方程形式：

对于 piecewise smooth curves（比如下图） 来说，它的计算也很简单，就是把各个部分的积分累加起来，公式如下：

∫Cf(x,y)ds=∫C1f(x,y)ds+∫C2f(x,y)ds+∫C3f(x,y)ds+∫C4f(x,y)ds

关于这种类型的曲线积分有以下2种性质：

1. Not Path-independence. 起点终点相同，但是积分路径不同，会导致不同的积分结果
2. 在同一条积分路径上，积分方向不会影响积分结果

line integrals with respect to x, y, and/or z

The line integral of f with respect to x is,

∫Cf(x,y)dx

The line integral of f with respect to x is,

∫Cf(x,y)dy

从上面的定义可以看出，它和对弧长的线积分唯一不同就是 differential. 上面的2种积分经常一起出现，因此通常用下面的 notation 去表示它们：

∫CP(x,y)dx+∫CQ(x,y)dy=∫CPdx+Qdy

对于这种类型的积分来说，积分方向相反会导致积分的结果相反，因此得到如下3种表达：

∫Cf(x,y)dx=−∫−Cf(x,y)dx∫Cf(x,y)dy=−∫−Cf(x,y)dy∫CPdx+Qdy=−∫−CPdx+Qdy

Line Integrals of Vector Fields

下图中是关于 Vector Fileds 的定义：

这种类型的积分定义如下：

∫CF⃗ ⋅dr⃗ =F⃗ ⋅T⃗ ds

• 上述公式中的 F⃗  是 vector field， F⃗ (x,y,z)=P(x,y,z)i⃗ +Q(x,y,z)j⃗ +R(x,y,z)k⃗ 
• 上述公式中的 r⃗  是位置向量， r⃗ =x(t)i⃗ +y(t)j⃗ +z(t)k⃗ 
• T⃗  是轨迹各处的切线方向， ds 是 dr⃗  的大小

那么我们如何求解这种类型的线积分呢？可以直接用下图中推导出的结果来求：

上图之所以 ds=||r′→(t)||dt ，是因为 speed 乘以时间等于路程。文章中 的例子给出了用这种方法求解的例子，很简单。

上面介绍的方法是直接求解，我们还有另一种方法也可以求解。由于 F⃗ =⟨P,Q,R,⟩,dr⃗ =⟨dx,dy,dz⟩ ，因此得：

∫CF⃗ ⋅dr⃗ =∫CPdx+Qdy+Rdz

从上面的结果可以看到，它同时也是一个 line integrals with respect to x, y, and z，因此这给我们另一种求解的方式。由于它也属于对坐标的线积分，因此它也具体如下性质：

沿路径积分的方向相反会导致积分结果相反

上述介绍的只是冰冷的公式，而 MIT 的教授在课上给出了物理意义，在下面的小节中，我把这些物理意义总结下来。

Fundamental Theorem for Line Integrals

In Calculus I we had the Fundamental Theorem of Calculus that told us how to evaluate definite integrals. This told us,

∫baF′(x)dx=F(b)−F(a)

这个定理与之类似。定理内容摘自 Fundamental Theorem for Line Integrals，同时这篇文章的内容也给出了定理的证明：

If F⃗ =∇f is a gradient field and C is any curve with endpoints P0=(x0,y0) and P1=(x1,y1) then:

∫CF⃗ ⋅dr⃗ =f(x1,y1)−f(x0,y0)

That is, for gradient fields the line integral is independent of the path taken, i.e., it depends only on the endpoints of C.

由于在梯度域中，积分的大小只取决于2个端点，因此如果路径是 closed 的，那么积分等于0，书写成如下公式：

∮CF⃗ ⋅dr⃗ =0

同样的，如果 for any closed curve 上述公式成立，那么也可以说明是 path independence. 上面的链接文章中有相应的证明，很简单。也就是说：path independence is equivalent to conservative.

Conservative Vector Fields

有了 Fundamental Theorem for Line Integrals，我们就可以很容易地求出曲线积分了。但是应用这个定理并不是无条件的，因此在这个小节中，主要解决以下2个问题：

1. 如何判断 F⃗  是否为 conservative vector fields？
2. 如果是的情况下，如何找到它的 potential function？

在回答第一个问题之前，先理解下面的准则：

Let F⃗ =Mi⃗ +Nj⃗  be continuously differentiable in a region D Then, in D ,

F⃗ =∇fforsomef(x,y)⇒My=Nx

上面得出的公式很容易证明：由于 f 在 i⃗  方向（即 x 轴方向）上的导数为 fx=M ，同理 fy=N ，又 fxy=fyx ，因此可证。

那么，上面的准则反过来是否成立呢？也就是说，如果 My=Nx,F⃗  是 conservative vector fields 吗？ 幸运的是，答案是肯定的，
Green’s Theorem and Conservative Fields 给出了证明，注意定理成立的条件。

现在已经知道如何判断 F⃗  是否为 conservative vector fields 了，接下来，我们来看看如何找到它的 potential function？下面2种方法可以做到这一点（具体细节参考：Gradient Fields and Exact Differentials）：

1、Fundamental Theorem for Line Integrals

∫(x,y)(x0,y0)F⋅dr⃗ =f(x,y)−f(x0,y0)⇒f(x0,y0)=c为常量

2、Antiderivatives

由于 F⃗ =∇f=⟨M,N⟩=⟨fx,fy⟩ ，因此 fx=M,fy=N ，知道了这些，通过固定的步骤（算法）就能得到答案了。具体算法很简单，通过一个 文章 中的例子2中的a，一下就能明白算法是什么了。

曲线积分在求物理量上的应用

曲线积分与做功

2D

在这个小节中，教授主要介绍了 force vector field 在给定的 trajectory 下做了多少功，这样的问题需要用到曲线积分来求解。下图是求解这个问题的主要思想，用点积是因为需要找出力在轨迹各个点的切线方向上做的功。

由于我们已经知道在轨迹上某一小段的做功表达，剩下的只需要沿着轨迹积分就能求出总体做的功。

W=∫CF⃗ ⋅dr⃗ 

由于 F⃗ =⟨M,N⟩ , dr⃗ =⟨dx,dy⟩ , 因此我们可以把上面的公式写成如下形式：

W=∫CF⃗ ⋅dr⃗ =∫CMdx+Ndy

由于这是单变量积分，而上面的公式中有2个变量，所以没法求解它。因此如果想要求解出上面的积分，需要把变量 x,y 参数化成同一个变量。当然了，你可以自由地选择任何你想要的变量，但是你应该选择使你解题最简单的那一个。

比如下图中的例子， x,y 被参数化成同一个变量 t ，下图中的 dr⃗ dt=⟨dxdt,dydt⟩ 实际上是 velocity vector.

当然了，如果你不想参数化成变量 t ，你也可以参数化成变量 x . 由于 y=x2,dy=2xdx ，然后你把所有关于变量 y,dy 全部替换成 x,dx 依然可以得到相同的结果。总之，你必须要把2个不同的变量用同一个变量表示，只有这样，才能求出积分。

3D

在 3D 中的做功与 2D 中的没有什么区别，只是多出一个 component，如下图所示：

求解上图中曲线积分的方法也和 2D 相似，参数化曲线 C ，用同一个变量表达 x,y,z,dx,dy,dz . 有些时候可能用时间 t 做为参数，而有些时候需要用角度 θ 来做参数，或者用 x,y,z 中的某个变量做参数。

在 3D 中，如何判断给定的 vector field F⃗  是否为 conservative 与 2D 有些不同，但大体思路不变。推导过程如下图所示：

从上图可以看出，与 2D 没什么区别，只不过是由于多出了一个 component，多出了2种组合，需要使各个组合的二阶导数相等，当然了如果超过3个变量也是同样的道理，只不过组合会变得更多。

如果知道 F⃗  是梯度 field 以后，如何找出 potential function 呢？和 2D 中的一样，一个方法是用曲线积分，另一个方法是 Antiderivatives. 参考 Gradient Fields in Space 中给出的详细步骤，一下就能明白这2种方法了，很简单，需要多加练习。

定理：如果 F⃗  是 conservative 的，那么 curlF⃗ =0

关于 curl 在 3D 中的公式，在下面我已经给出了，Del 操作符来帮助我们记住它的公式。

通量

Flux 也属于曲线积分的一种，它的积分公式如下：

∫CF⃗ ⋅n^ds

那么如何解释上面的公式呢？如果 F⃗  为 velocity field 的情况下，通量测量着 how much fluid passes through curve C per unit time. 下图是微分观的放大，清晰地解释了为什么 integrand 是上面公式的样子。更详细的解释看 Lec 23 9:06-15:00.

那么现在的问题是，我们应该如何求出上面的曲线积分呢？其实很简单，如下图所示：

下图是我用手画的，顺时针或逆时针旋转坐标发生的变化，方便理解上图中的坐标变化。

因此，如果 F⃗ =⟨P,Q⟩ ，那么

∫CF⃗ ⋅n^ds=∫C⟨P,Q⟩⋅⟨dy,−dx⟩=∫C−Qdx+Pdy

做功与通量之间的比较

对于数学家来说，它们都只是线积分的计算，没什么区别;但是从物理学家的角度来看，它们度量的是不同的物理量。由于测量的物理量不同，导致它们下图所示的不同：

接下来，我们来看一下格林定理分别应用到它们身上会有什么不同的结果。在下个小节中给出格林定理的定义，给出了线积分与二重积分之间的关系。这里我们只需要机械地把它们各自的表达公式代入定理之中，从而看看得到什么结果。假设 F⃗ =⟨P,Q⟩ ，它们各自的表达公式如下：

通量：∫CF⃗ ⋅n^ds=∫C−Qdx+Pdy做功：∫CF⃗ ⋅T^ds=∫CPdx+Qdy

把它们分别代入到格林要定理之中(注意区分每个字母所代表的 component)，得：

通量：∮CF⃗ ⋅n^ds=∬R(Px+Qy)dA=∬RdivF⃗ dA做功：∮CF⃗ ⋅T^ds=∬R(Qx−Py)dA=∬RcurlF⃗ dA

Curl and Divergence

Del 操作符

严格来说，del 不是一个具体的操作符，而是一个方便的数学记号便于书写和记住一些等式。在三维空间直角坐标系下，它可以记作 ∇=⟨∂∂x,∂∂y,∂∂z⟩

Del is used as a shorthand form to simplify many long mathematical expressions. It is most commonly used to simplify expressions for the gradient, divergence, curl, directional derivative, and Laplacian.

1. The vector derivative of a scalar field f is called the gradient, and it can be represented as: gradf=⟨∂f∂x,∂f∂y,∂f∂z⟩=∇f
2. The divergence of a vector field v⃗ =⟨P,Q,R⟩ is a scalar function that can be represented as: divv⃗ =∂P∂x+∂Q∂y+∂R∂z=∇⋅v⃗ 
3. The curl of a vector field v⃗ =⟨P,Q,R⟩ is a vector function that can be represented as: curlv⃗ =⎡⎣⎢⎢i⃗ ∂∂xPj⃗ ∂∂yQk⃗ ∂∂zR⎤⎦⎥⎥=∇×v⃗ 

Divergence

这个小节的内容来自于对 Divergence 的总结。

为了更好的理解 divergence，解释 a vector field as representing a fluid flow. 在流体流动的过程中，有些区域变得 less dense，而有些区域变得 more dense，或者 dense 保持不变。Divergence 可以测量这些区域的 change in density. 下图就是 divergence 对各种情况的解释：

从上图可以看出，当 divergence 小于0时，区域会变得 more dense，依此依此类推。我们也可以从 “Sources and sinks” 的观点来看待上面的现象：negative divergence are often called “sinks”，positive divergence are often called “sources”. 当然了，上图中只是二维的描述，三维空间也是同样的道理。

因此 divergence 的物理解释可以总结为：

If we think of v⃗  as the velocity field of a flowing fluid, then divv⃗  represents the net rate of change of the mass of the fluid flowing from the point (x,y,z) per unit volume. This can also be thought of as the tendency of a fluid to diverge from a point.

Curl

Curl 的计算方法在 “Del 操作符 “小节中已经给出了。我们可以把 curl 看成是一个 operator：It takes in a function representing a three-dimensional vector field, and gives another function representing a different three-dimensional vector field.

Curl 的物理解释：If a fluid flows in three-dimensional space along a vector field, the rotation of that fluid around each point, represented as a vector, is given by the curl of the original vector field evaluated at that point. The curl vector field should be scaled by a half if you want the magnitude of curl vectors to equal the rotational speed of the fluid.

Suppose that v⃗  is the velocity field of a flowing fluid. Then curlv⃗  represents the tendency of particles at the point (x,y,z) to rotate about the axis that points in the direction of curlv⃗ 

Green’s Theorem

格林定理实际上就是关于特定类型的线积分(on closed paths)与二重积分之间的关系。格林定理必须满足下面几个要素：

• C a simple closed curve (simple means it never intersects itself)
• R the interior of C
• C must be positively oriented（就是当你沿着路径方向走的时候，区域总会在你的左侧）
• C must be piecewise smooth

下图是符合上面要素的例子：

格林定理内容如下：

With the above ingredients for a vector field F⃗ =⟨M,N⟩ we have:

∮CMdx+Ndy=∬RNx−MydA

由于二维平面 curl 的定义为 curlF⃗ =Nx−My ，因此我们也可把定理写成如下形式：

∮CF⃗ ⋅dr⃗ =∬RcurlF⃗ dA

关于格林定理的证明参考：Proof of Green’s Theorem

如果区域存在 holes，我们照样可以应用格林定理，正如下图所示，我们可以把中间的 hole 连通，边界由于方向相反，它们的积分可以抵消掉。对于有 hole 的这种，你要注意的就是二重积分的边界会发生改变，也就是区域 R 发生了变化。

Green’s Theorem 的例子3就是一个关于有 hole 的例子，并且这篇文章中有详细的推导步骤为什么有 hole 的情况依然可以应用格林定理。

同样的道理，比如我想求出下图中的曲线积分，由于它们都是 positively oriented，因此我们可以得： ∫C1F⃗ ⋅dr⃗ +∫C2F⃗ ⋅dr⃗ +∫C3F⃗ ⋅dr⃗ +∫C4F⃗ ⋅dr⃗ =∬RcurlFdA ，如果没有这3个 holes，区域就是整个 C4 内部。

Triple integrals 和坐标系

Triple integrals 的基本形式如下：

∭RfdV

• R is some region in three-dimensional space
• f(x,y,z) is some scalar-valued function which takes points in three-dimensional space as its input
• dV is a tiny unit of volume

像二重积分一样，难点就是为它找到恰当的边界，这需要多加练习。在下面不同的坐标系中，我们主要的任务就是如何表示 dV

Triple integrals in Rectangular coordinates

在普通的空间直角坐标系中，我们已经知道 dV=dxdydz ，因此三重积分写成如下形式：

Triple integrals in cylindrical coordinates

柱面坐标系其实有点类似于 2D 中的极坐标系，只不过现在多了 z 坐标。从下图我们可以看出 dV=rdθdrdz

Khan academy 中有关于柱面坐标系的例子。 Using cylindrical coordinates can greatly simplify a triple integral when the region you are integrating over has some kind of rotational symmetry about the z -axis.

Triple integrals in spherical coordinates

球坐标系的表示如下图所示，接下来的问题就是，如何用下图中的3个变量表示 dV 呢？

从下图可以看出，每一个 tiny volume 表示出如下形式，因此在球坐标系下的三重积分可以表示为：

Converting to spherical coordinates can make triple integrals much easier to work out when the region you are integrating over has some spherical symmetry.

物理应用：万有引力

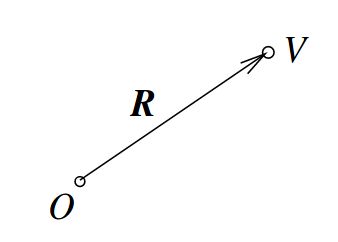
下图中有2个 point mass，其中一个在原点，它们的 mass 分别为 m1,m2 ，它们之间的引力（大小和方向）为：

F⃗ =Gm1m2|R⃗ |2r⃗ 

• 力的大小为 Gm1m2|R⃗ |2 ，其中 G 为常量
• 力的方向为 r⃗ =R⃗ |R⃗ |

然而，如果不在原点的那个物体有体积的情况下，我们必须要用到积分，因为物体各处对原点 point mass 的引力不相同。有了上面的基础，可以很容易地写出关于引力的积分,假设原点的 point mass 为 m ，公式如下：

F⃗ =∭RGmdM|R⃗ |2⟨x,y,z⟩x2+y2+z2−−−−−−−−−−√=∭RGmδdV|R⃗ |2⟨x,y,z⟩|R⃗ |

由于上述公式中的 integrand 存在向量，想要求出结果，必须分别对每个 component 进行积分，从而得到引力的各个 component. 比如，现在我只想求 z component 的引力，因此方向就变成了 ⟨x,y,z⟩|R⃗ |⋅k^=R^⋅⟨0,0,1⟩=|R^||k^|cosϕ=cosϕ ，这里面向量 R⃗  的大小相当于球坐标系中的 r ，而 ϕ 为它与 z 轴之间的夹角。有了这些，积分可以改写成如下形式：

F⃗ =∭RGmdM|R⃗ |2⟨x,y,z⟩x2+y2+z2−−−−−−−−−−√⋅k^=∭RGm|R⃗ |2cosϕδdV=Gm∭R1|R⃗ |2cosϕδρ2sinϕdρdϕdθ=Gm∭Rcosϕδsinϕdρdϕdθ

Surface Integrals

Flux in 3D

其实它和 2D 的通量没有什么太大的区别，主要就是 infinitesimal element 不同，3D 是无限小的曲面面积，而 2D 是无限小的曲线长度。下图中， F⃗  是空间的 vector field，而 S 是空间中的一个曲面， n^ 是 曲面 S 的 unit normal vector，它的方向只有2个选择（选择任意一个都可以）。

下图是它的几何解释：

知道了如何表示通量，接下来我们需要知道如何求解它。下面几幅图是教授总结关于在特殊曲面上如何找出 n^ 和 dS

下图是关于如何在球体和柱体中找出 n^ 和 dS ，Surface Integrals 里面有2个具体的例子，都有具体的步骤，看一下就可以明白如何求解这样的曲面积分了。

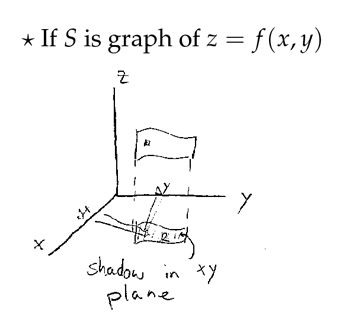
正如教授所说，我们的生活中并不只有这些特殊形体，那么如何求解在一般形体上的曲面积分呢？在上面介绍的特殊形体中，都是把 n^ 和 dS 分开来找，但是对于一般的形体来说，把它们结合起来一起表达更容易，也就是说： n^dS=dS⃗  ，下图就是一般的形体，关于曲面的函数是任意的 z=f(x,y) ，之所以对其进行投影，是想找出 dx,dy 的 bounds.

下图就是表达 dS⃗  的公式，Surface Integrals 中给出了2个公式的证明，并且其中的例子3和例子4分别是针对下面2个公式的例子。

上面公式的证明其实很简单，下图是对老师课上证明的总结，它是对上图中 11a 的证明，通过 11a，用链式法则和求导就能推导出 11b，详细步骤就参考上面那个文章吧！

---

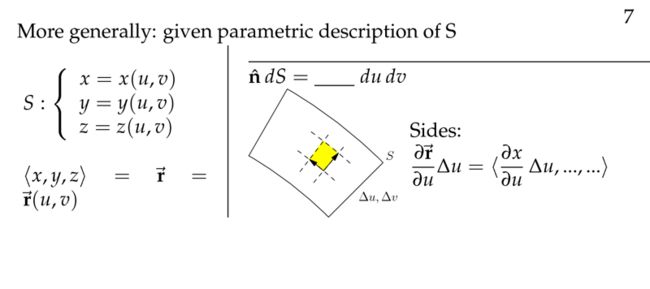
在上面的内容中，假设我们的曲面已经可以用 z=f(x,y) 来表示。但是，对于一些十分复杂的曲面来说，我们只知道它的参数化表示形式。就像曲线一样，比如圆形曲线，你可以写成 x2+y2=a ，你也可以用另外一个变量把它参数化。只不过现在是曲面，需要2个变量来参数化。假设现在有个曲面，它的参数化表达如下图左侧所示：

因此，位置向量 r⃗  只取决于变量 u,v ，看上图黄色的部分，当我固定其中一个变量，改变另一个变量时，位置向量 r⃗  是如何变化的，因此分别得： ∂r⃗ ∂uΔu=⟨∂x∂uΔu,∂y∂uΔu,∂z∂uΔu⟩ ，同样的道理可得： ∂r⃗ ∂vΔv=⟨∂x∂vΔv,∂y∂vΔv,∂z∂vΔv⟩ ，求出了2边的向量，用 cross product 就可以求出 n^dS 了：

---

在上面的情况中，我们都已经知道曲面的方程或其参数化形式。但是，如果我只知道曲面的 normal vector 呢？我依然可以找出 n^dS ，当然了，如果知道 normal vector 以后，你可以找出曲线方程，然后用上面给出的方法。但是，这种方式会更简单，不需要找原方程。下图是2个法向量与原方程关系的例子，在文章最上面，我已经介绍了梯度垂直于 level surface.

下面2幅图给出了找 n^dS 的过程，很清晰，没什么好解释的了。注意：下图的那个斜面是 ΔS ，不是整个曲面。

下图是一个把上图中公式应用到 z=f(x,y) 的一个例子，你会发现结果和上面证明的一样：

Calculating general surface integrals

如果已经明白了如何求通量，求一个普通的曲面积分就很简单了。由于 n^dS=dS⃗  ，因此 dS 就是 dS⃗  的大小，通过上面的 11a 和 11b 就可以得到如下2个公式了：

Divergence Theorem

上面我介绍了很多方法来求解曲面积分，而这个定理让我们在某些情况下，可以避免求解曲面积分。下面2幅图是 Divergence Theorem 的内容：

下图是一个应用 Divergence Theorem 的例子：

Proof of the Divergence Theorem

Stokes’ theorem

Stokes’ theorem is the 3d version of Green’s theorem, relating the surface integral of a curl vector field to a line integral around that surface’s boundary.

为了更直观的理解上面的公式，可以把上述公式中的 S 和 C 理解成下图中的关系，起初有个闭合的的 curve C ，然后起泡一个 surface S ，这个表面 S 可以是任意的，当然了应该选择一个最容易计算曲面积分的 surface。你会发现，公式中的右半部分正是 Flux in 3D 中的公式，也就是说，它计算的实际上是通量，vector field 是 curlF⃗  。为什么是这样呢？

还有一个就是方向的问题，也就说，curve C 和 surface S 的 orientations 应该是 compatible 的，不然最终的结果会相反 by -1. 从上图可以看出，curve C 的方向有2个（顺时针和逆时针），同样 surface S 的 normal vector 也有2个方向（向内或向外）。如何使它们的方向 compatible 呢？假设我先指定 surface S 的 normal vector 向外，让你的头部与它的方向一致，然后沿着 curve C 走，使得 surface 在你的左部。如果先指定 surface S 的 normal vector 向内，也是同样的道理。可以看一下 Khan 的视频讲解 Orientation and stokes

Green’s theorem 是 Stokes’ theorem 的一个特例。不信的话看下图，有一个 curve C 在 x−y 平面上，由于我上面已经说了，可以起泡任意的 surface S ，这里我就让 surface S 是曲线内部的区域，用 Stokes’ theorem 来计算这个积分，最终会得到 Green’s theorem 的公式，详细计算步骤参考 Stokes’ Theorem 文章中间的部分。

总结

下图是对整个多变量微积分中3个最重要的难点总结，并给出了 divergence theorem 和 Stokes’ theorem 作为桥梁把它们之间连接起来。