特征抽取篇之Isomap(Isometric Mapping)
前言
Isomap,中文名叫“等度量映射”,是一篇发表在超一流期刊Science的大作。据百度学术的数据显示,截止2019年4月,它的被引量已经高达1.3万。作为一种降维算法,它同样可以应用于降维、可视化等领域。Isomap算法核心在于发现并利用流形空间的特点,引入测地线距离和提出对应的距离计算方法。相信本文能对一些对降维和距离度量学习的朋友有所帮助。
准备知识
流形
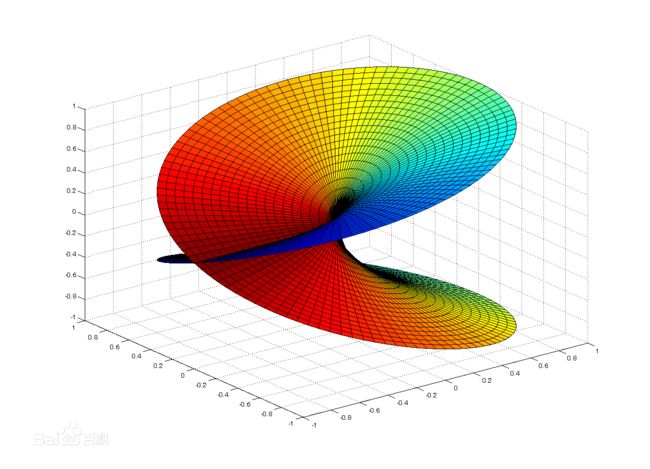
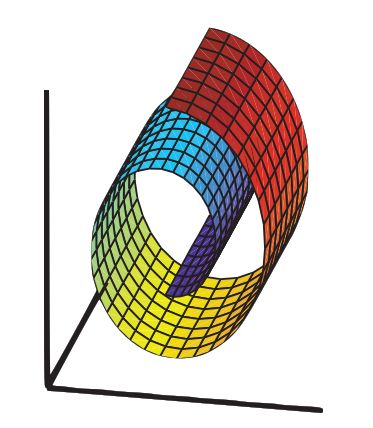
流形是在局部区域与欧氏空间同胚的空间,即在局部区域具有欧氏空间的性质,能用欧氏距离来进行距离计算。下面两幅流形图片可以给你一个直观的认识:
数据结构-图论:计算两点间的最短距离
有一定数据结构基础的朋友一定知道,这个问题通常用来求解的算法是:迪杰斯特拉和弗洛伊德算法。在此,我强调的是它们各自的前提条件,Dijkstra算法要求图中路径长度必须大于等于0,Floyd算法只要求没有总和小于0的环路。庆幸地是,在Isomap算法中不存在这两种异常情况。
算法思想
Isomap算法没有多少公式推导的内容,它的创新点是引入测地线距离和提出对应的距离计算方法。此算法出发点,是认识到流形在高维空间中,两个样本之间的距离不该直接使用欧式距离计算直线距离,更应该是采用“测地线”距离:就像我们日常生活中送快递的例子,两个城市之间如果没有直达的路线,快递就会经过许多中转站才能送到。测地线距离就是讲这样的距离,下图中的红线和黑线可以直观地告诉你测地线距离与直线距离的区别。
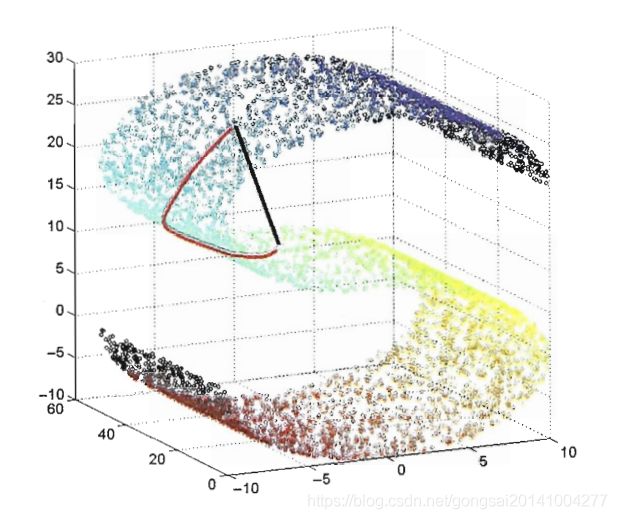
其中,红线长度是测地线距离,黑线长度是欧式距离。
直观上,在流形空间中,较远的两个点之间测地线距离更适用。那么接下来便有两个问题:一,如何确定局部这个范围?二,如何计算测地线距离呢?Isomap算法对这两个问题给出了一份答案,前者使用K近邻的思想确定局部范围;后者采用最短路径算法计算测地线距离。就这样,我们可以得到一个距离矩阵,接下来便把这个距离矩阵当做MDS算法(上一篇文章)的输入,从而实现降维任务。
算法步骤
输入:样本集 D = { x 1 , x 2 , ⋅ ⋅ ⋅ , x m } D=\{\boldsymbol x_1,\boldsymbol x_2,\cdot\cdot\cdot,\boldsymbol x_m\} D={x1,x2,⋅⋅⋅,xm};近邻参数 k k k;低维空间维数 d ′ d' d′。
步骤:
1:for i=1,2,…,m do
2: 确定 x i \boldsymbol x_i xi的 k k k近邻;
3: x i \boldsymbol x_i xi与 k k k近邻点之间的距离设置为欧式距离,与其他点的距离设置为无穷大;
4:end for
5:调用最短路径算法计算较远两个样本点之间的距离 d i s t i j dist_{ij} distij;
6:将距离矩阵 D i s t Dist Dist作为MDS算法的输入;
7:return MDS算法的输出
输出:样本集 D D D在低维空间的投影 Z = { z 1 , z 2 , ⋅ ⋅ ⋅ , z m } Z=\{ \boldsymbol z_1,\boldsymbol z_2,\cdot\cdot\cdot,\boldsymbol z_m \} Z={z1,z2,⋅⋅⋅,zm}。
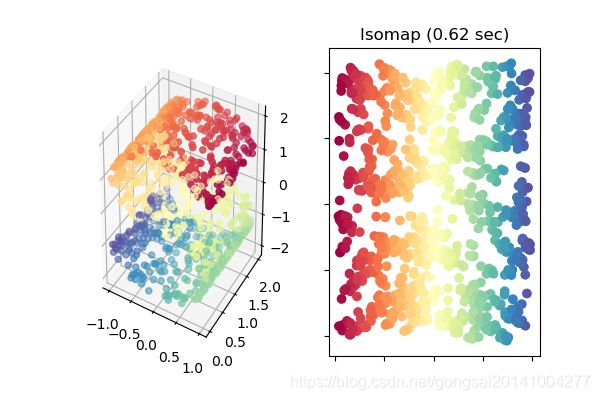
实验效果
调用sklearn库
"""
Isomap : Isometric mapping
Refercences :
[1]周志华.机器学习[M].清华大学出版社,2016:425.
[2]http://scikit-learn.sourceforge.net/dev/modules/generated/sklearn.manifold.Isomap.html
Author : Ggmatch
Date : 2019/4/12
"""
from time import time
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.ticker import NullFormatter
from sklearn import manifold, datasets
# 制造样本
n_points = 1000
X, color = datasets.samples_generator.make_s_curve(n_points, random_state=0)
n_neighbors = 10
fig = plt.figure(figsize=(6, 4)) #画板
gs = fig.add_gridspec(1,2) #共2副子图
ax1 = fig.add_subplot(gs[0,0], projection='3d') #第一幅子图表示原始样本分布
ax1.scatter(X[:, 0], X[:, 1], X[:, 2], c=color, cmap=plt.cm.Spectral)
# Isomap降维
n_components = 2
t0 = time() #计时开始
Y = manifold.Isomap(n_neighbors, n_components).fit_transform(X)
t1 = time() #计时结束
ax2 = fig.add_subplot(gs[0,1])
ax2.scatter(Y[:, 0], Y[:, 1], c=color, cmap=plt.cm.Spectral) #第2副子图表示降维后样本分布
ax2.set_title("Isomap (%.2g sec)" % (t1 - t0))
ax2.xaxis.set_major_formatter(NullFormatter())
ax2.yaxis.set_major_formatter(NullFormatter())
plt.show()
实验效果
总结
1)Isomap算法对比MDS算法的实验效果,可以看出经过Isomap算法降维过的样本更有利于后续分类算法学习;
2)Isomap算法并非无懈可击,其中k近邻思想的引入,使之更具灵活性,但也不免带来弊端,就是需要针对具体任务来进行人工调参。
参考文献
[1]Tenenbaum J B, De V S, Langford J C. A global geometric framework for nonlinear dimensionality reduction.[J]. Science, 2000, 290(5500):2319-2323.
[2]https://baike.baidu.com/item/流形/2884058?fr=aladdin
[3]周志华.机器学习[M].清华大学出版社,2016:425.
[4]http://scikit-learn.sourceforge.net/dev/modules/generated/sklearn.manifold.Isomap.html#sklearn.manifold.Isomap