「HNOI2014」世界树 虚树

「HNOI2014」世界树

前置技能：虚树。

（本题可以通过以下相似的思想用线段树维护子树信息和倍增找中点完成，代码短很多，但本篇题解不涉及）

题解部分

这种总询问点数不大，但是询问次数多，可以想到用虚树来优化。

我们把所有询问点看成关键点建一颗虚树。对于虚树上的点我们是可以求出离它最近的点。那么对于那些被隐藏的点。这里有两种被隐藏的点。（以下为有根树）

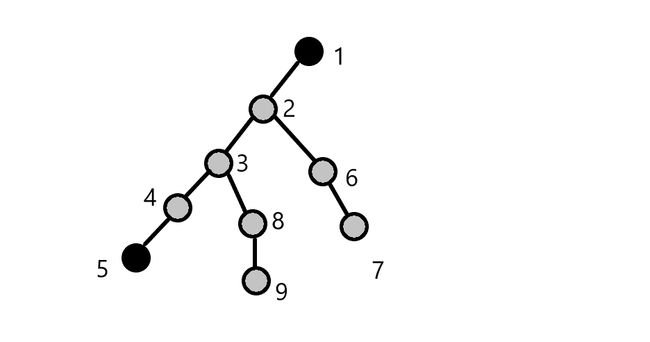
其中黑色和橙色的为虚树上的点，灰色的就是被隐藏的点。对于这些被隐藏的点，离他们最近的临时议事处就是离橙色的点最近的临时议事处。这个可以通过维护一个sz数组，sz[i]表示i在原树中的子树的节点个数。那么答案就是sz[1]减去所有P类子节点的sz（P类子节点就是这个子节点的子树在虚树中有出现，P类这个名字是乱取的）

已知点1,5为虚树上的点，其他点为虚树上的点，点1的深度较低。我们如果知道了不在2的子树内的离1最近的临时议事处离1的距离及其编号，也知道5的子树内的离5距离最近临时议事处的的距离及其编号。对于1,到5这条链上的点，那么我们就可以求出一个深度临界值，在这个深度及其以上的都被离1最近的临时议事处所管辖，在这个深度以下的都被离5最近的临时议事处所管辖。由于像8,9的这些点，他们归属的临时议事处和他们所对应的链上的点（如8,9对应3）是一样的，故和他们一起考虑。

那么我们要预处理出每个点子树内离它最近与次近的临时议事处，每个点子树内除它和除它子树内节点离他最近的临时议事处。用每个点子树内离它次近的临时议事处与每个点除子树内节点离他最近的临时议事处就可求出每个点除任意一个子节点的子树外离它最近的临时议事处。

记离5最近的临时议事处编号为X，离1最近的临时议事处编号为Y。

假设3,4归X管辖，2归Y管辖。那么X管辖这一部分的点数为sz[3]-sz[5]，Y管辖这一部分的点数为sz[2]-sz[3]。（这里可以用倍增的方式维护父亲，就可以找到1,5这条链上1的子节点）

#include
#include
#include
#include
#define M 300005
using namespace std;
struct E{
	int to,nx;
}edge[M<<1];
int tot,head[M];
void Addedge(int a,int b){
	edge[++tot].to=b;
	edge[tot].nx=head[a];
	head[a]=tot;
}
int fa[M][20],dep[M],sz[M];
int Dfn[M],tot_id;
void dfs_Init(int now){
	sz[now]=1;
	Dfn[now]=++tot_id;//预处理DFS序 
	for(int i=1;i<20;i++)fa[now][i]=fa[fa[now][i-1]][i-1];//倍增的fa数组 
	for(int i=head[now];i;i=edge[i].nx){
		int nxt=edge[i].to;
		if(nxt==fa[now][0])continue;
		fa[nxt][0]=now;
		dep[nxt]=dep[now]+1;
		dfs_Init(nxt);
		sz[now]+=sz[nxt];
	}
}
int Up(int x,int y){//求x这个点的第y个父亲 
	for(int i=0;i<20;i++)if((1<<i)&y)x=fa[x][i];
	return x;
}
int LCA(int x,int y){//倍增求LCA 
	if(dep[x]<dep[y])swap(x,y);
	x=Up(x,dep[x]-dep[y]);
	if(x==y)return x;
	for(int i=19;i>=0;i--){
		if(fa[x][i]!=fa[y][i])x=fa[x][i],y=fa[y][i];
	}
	return fa[x][0];
}
bool cmp_dfn(int x,int y){
	return Dfn[x]<Dfn[y];
}
int stk[M];
int tmp[M];
void i_Build(int Q[],int len){//建虚树 
	for(int i=1;i<=len;i++)tmp[i]=Q[i];
	sort(tmp+1,tmp+len+1,cmp_dfn);//按dfs序排序 
	int top=0;
	if(tmp[1]!=1)stk[++top]=1;
	for(int i=1;i<=len;i++){
		if(top<=1){stk[++top]=tmp[i];continue;}
		int lca=LCA(tmp[i],stk[top]);
		if(lca==stk[top]){stk[++top]=tmp[i];continue;}
		while(top>1&&Dfn[lca]<=Dfn[stk[top-1]]){
			Addedge(stk[top-1],stk[top]);
			top--;
		}
		if(stk[top]!=lca){
			Addedge(lca,stk[top]);
			stk[top]=lca;
		}
		stk[++top]=tmp[i];
	}
	while(top>1){
		Addedge(stk[top-1],stk[top]);
		top--;
	}
}
bool mark[M];
int Q[M];
int Near[M][2];//Near[i][0]在这个点下面的离它最近的 1在这个点上面
int dis[M][2];
int se_near[M],se_dis[M]; 
bool check(int x,int y,int a){//y这个点是否比x离a更近(这里的x，y分别于a有祖先关系） 
	if(x==0)return 1;
	if(y==0)return 0;
	int dis1=abs(dep[x]-dep[a]),dis2=abs(dep[y]-dep[a]);
	if(dis1==dis2)return y<x;
	return dis2<dis1;
}
bool check(int x,int dis1,int y,int dis2){//y这个点是否比x离a更近
	if(x==0)return 1;
	if(y==0)return 0;
	if(dis1==dis2)return y<x;
	return dis2<dis1;
}
void dfs_low(int now){//预处理出一个点的子树内离他最近和次近的临时议事处 
	int &res=Near[now][0];
	int &res0=se_near[now];
	dis[now][0]=1e9;
	se_dis[now]=1e9;
	res=res0=0;
	if(mark[now])res=now;
	for(int i=head[now];i;i=edge[i].nx){
		int nxt=edge[i].to;
		dfs_low(nxt);
		if(check(res,Near[nxt][0],now))res0=res,res=Near[nxt][0];
		else if(check(res0,Near[nxt][0],now))res0=Near[nxt][0];
	}
	if(res)dis[now][0]=dep[res]-dep[now];
	if(res0)se_dis[now]=dep[res0]-dep[now];
}
void dfs_upp(int now,int pre,int pre_dis){//预处理一个点除它和它子树的点离他最近的临时议事处 
	int &res=Near[now][1];
	dis[now][1]=1e9;
	res=0;
	if(mark[now]){
		res=now;
		dis[now][1]=0;
		pre=now;
		pre_dis=0;
	}else res=pre,dis[now][1]=pre_dis;
	for(int i=head[now];i;i=edge[i].nx){
		int nxt=edge[i].to;
		int nxt_near=pre,nxt_dis=pre_dis;
		if(Near[nxt][0]==Near[now][0]){//求除nxt的子树外其他now子树的点离now的最近的临时议事处 
			if(check(nxt_near,nxt_dis,se_near[now],se_dis[now]))nxt_near=se_near[now],nxt_dis=se_dis[now];
		}else if(check(nxt_near,nxt_dis,Near[now][0],dis[now][0]))nxt_near=Near[now][0],nxt_dis=dis[now][0];
		dfs_upp(nxt,nxt_near,nxt_dis+dep[nxt]-dep[now]);//注意这里的两点间的距离不是1而是 dep[nxt]-dep[now] 
	}
}
int Ans[M];
void dfs_ans(int now){
	int mx_Near;
	if(check(Near[now][1],dis[now][1],Near[now][0],dis[now][0]))mx_Near=Near[now][0];
	else mx_Near=Near[now][1];
	int add=sz[now];
	for(int i=head[now];i;i=edge[i].nx){
		int nxt=edge[i].to;
		//决策now到nxt这条边上（对应原树）的点（不包括两端）
		int cnt=dep[nxt]-dep[now]-1,top,now_son,val,dis1,dis2,del_dis;
		//cnt为这条链上不包括两端的点的数量，now_son表示now到nxt的链上now的子节点。
		//dis1表示nxt子树内到nxt的最近的临时议事处到nxt的距离（这个点的编号记为X） 
		//dis2表示除now_son及其子树内的点到now的最近的临时议事处到now的距离 （这个点的标号记为Y） 
		//del_dis表示dis2-dis1 
		//val表示Y可以控制多少个now到nxt的链（原树上）上（不包括端点）的点
		//top Y能控制深度最浅的now到nxt的链上的点的编号 
		int up_Near=Near[now][1],up_dis=dis[now][1];//求出除nxt所对应now的子节点的子树的点外离now最近的临时议事处 
		if(Near[now][0]==Near[nxt][0]){if(check(up_Near,up_dis,se_near[now],se_dis[now]))up_Near=se_near[now],up_dis=se_dis[now];}
		else if(check(up_Near,up_dis,Near[now][0],dis[now][0]))up_Near=Near[now][0],up_dis=dis[now][0];
		if(cnt>0){
			dis1=dis[nxt][0],dis2=up_dis,del_dis=dis2-dis1;
			if(abs(del_dis)>=cnt){
				if(del_dis>=0)val=cnt;
				else val=0;
			}else {//减去del_dis后平均分配，若为奇数则编号小的那个多1 
				if(del_dis>0)val=del_dis+floor(1.0*(cnt-del_dis)/2.0);
				else if(del_dis<=0)val=floor(1.0*(cnt+del_dis)/2.0);
				if((cnt-abs(del_dis))%2==1&&Near[nxt][0]<up_Near)val++;
			}
			val=max(val,0); 
			top=Up(nxt,val),now_son=Up(nxt,dep[nxt]-dep[now]-1);
			Ans[Near[nxt][0]]+=sz[top]-sz[nxt];//计算答案 
			Ans[up_Near]+=sz[now_son]-sz[top];
		}else now_son=Up(nxt,dep[nxt]-dep[now]-1);
		add-=sz[now_son];
		dfs_ans(nxt);
	}
	Ans[mx_Near]+=add;//算题解中所说的情况1的答案 
}
void dfs_clear(int now){
	for(int i=head[now];i;i=edge[i].nx){//清空 
		dfs_clear(edge[i].to);
	}
	head[now]=0;
}
int main(){
	int n,m;
	scanf("%d",&n);
	for(int i=1;i<n;i++){
		int a,b;
		scanf("%d%d",&a,&b);
		Addedge(a,b);
		Addedge(b,a);
	}
	dfs_Init(1);
	memset(head,0,sizeof(head));tot=0;
	scanf("%d",&m);
	while(m--){
		int q;
		scanf("%d",&q);
		for(int i=1;i<=q;i++)scanf("%d",&Q[i]),mark[Q[i]]=1,Ans[Q[i]]=0;
		i_Build(Q,q);
		dfs_low(1);
		dfs_upp(1,0,1e9);
		dfs_ans(1);
		for(int i=1;i<=q;i++)printf("%d ",Ans[Q[i]]),mark[Q[i]]=0;
		puts("");
		dfs_clear(1);tot=0;
	}
	return 0;
}