线性代数的本质（笔记内容 by Mr. Aries）
线性代数的本质
- 1 向量究竟是什么？
- 2 线性组合、张成的空间与基
- 3 矩阵与线性变化
1 向量究竟是什么？
物理专业学生的角度
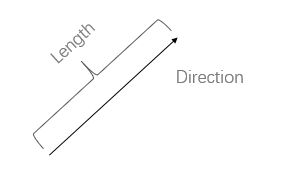
vectors are arrows pointing in space
只要以上的两个特征相同，你可以自由移动一格向量而保持它不变
计算机专业学生的视角
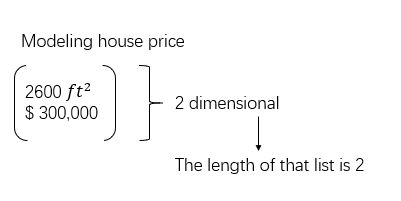
vectors are ordered lists of number
数学家
向量可以表示任何东西，只要保证两个向量相加以及数乘是有意义的
在线代中，向量通常以原点作为起点
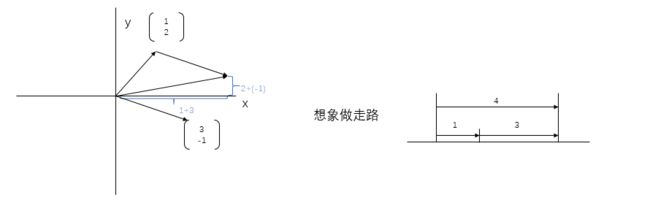
一个向量的坐标由一对数构成，这对数指导你如何从向量起点出发到达它的尖端（向量终点）
两个向量相加
( 1 2 ) + ( 3 − 1 ) = ( 1 + 3 2 + ( − 1 ) ) \binom{1}{2}+\binom{3}{-1}= \binom{1+3}{2+(-1)} (21)+(−13)=(2+(−1)1+3)
数乘
Scaling，几何角度看是缩放，实际上是数乘
In fact，throughout linear algebra，one of the main things that numbers do is scale vectors
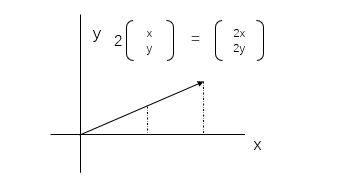
实际上无论你如何看待向量都是可以的，或把向量看做空间中的箭头（这种观点恰好有漂亮的数值表示与之对应），或把向量看做数字列表（这种观点又恰好有漂亮的几何意义与之对应），线代的效用很少体现在这些观点的其中一个上，而更多地体现在它能够在这些观点中相互转化
e.g.
（1）线代为数据分析提供了一条将大量数据列表概念化、可视化的渠道
（2）线代给物理学家和计算机图形程序员提供了一种语言通过机器能处理的数字来描述并操作空间
2 线性组合、张成的空间与基
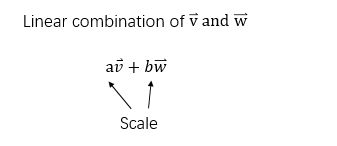
The idea of adding together two scaled vectors
we could have chosen different basis vectors，and gotten a completely reasonable，new coordinate system
每当我们用数字描述向量时，它都依赖于我们正在使用的基
如果固定其中一个标量，让另一个标量自由变化，所产生的向量的终点会描绘出一条直线
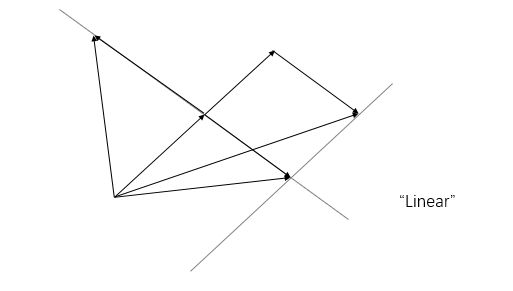
（1）大部分情况下，对于一对初始向量，你能到达平面中的每一个点，所有二维点尽在掌握
（2）当两个初始向量恰好共线时，所产生的向量终点被限制在一条直线上
（3）两个都是零向量，那就只能乖乖待在原点上了
vector vs. point
想象所有二维向量填满平面时，将会变得十分的拥挤。所以，为了应对这种情况，通常我们就用向量的终点代表向量
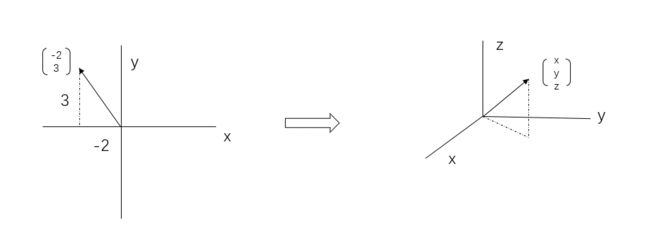
what does the span of 3d vectors look like ?
（1）如果第三个向量恰好落在前两个向量所张成的平面上，它们所张成的空间不变，仍是一个平面
（2）当如果随机选一个向量，它几乎不可能落在前两个向量所张成的平面中，这样由于第三个向量指向不同的方向，我们就能得到所有的三维向量
Linear dependent（线性相关）
你有多个向量，并且可以移除其中一个而不减小张成的空间，当这种情况发生时，我们称它们 “线性相关的”
换句话说，也就是其中一个向量可以表示为其他向量的线性组合，因为这个向量已经落在其他向量张成的空间中
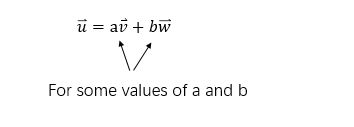
另一方面，如果所有向量都给张成的空间增添了新的维度，它们就被称为是 “线性无关的”
Technical definition of basis（基）
A basis of a vector space is a set of linearly independent vectors that span the full space
向量空间的一组基是张成该空间向量的一个线性无关向量组
3 矩阵与线性变化
如果一个变换具有以下两条性质，我们就称它是线性的：
- 直线变换后任然保持为直线
- 原点保持固定
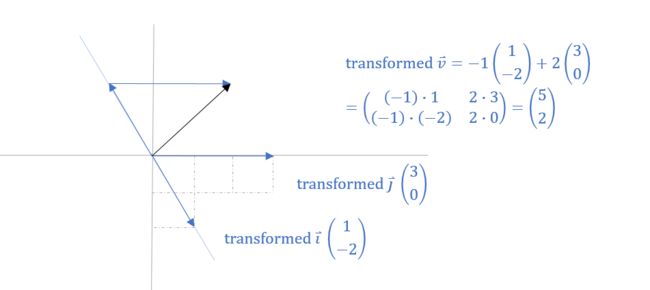
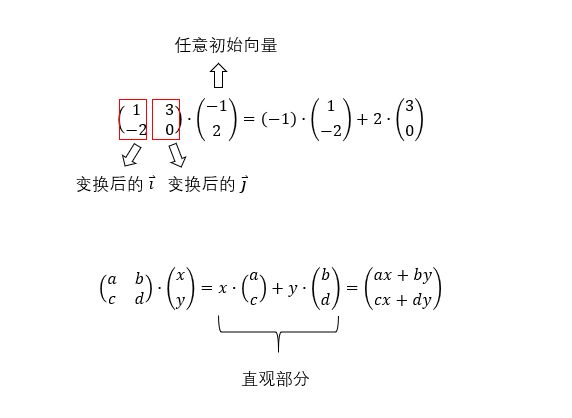
How would you describe one of these numerically ？
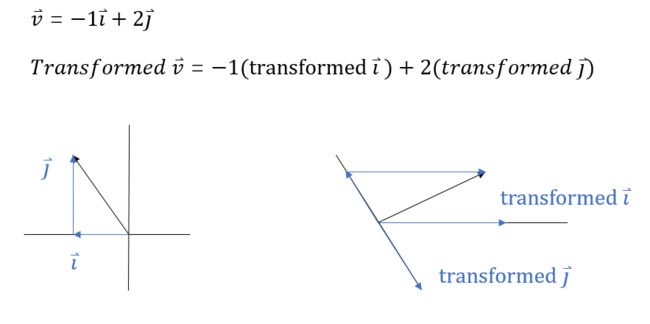
那么你可以只根据变换后的 i ⃗ \vec{i} i 和 j ⃗ \vec{j} j 就推出变化后的 v ⃗ \vec{v} v
