ButterWorthFIlter(巴特沃斯滤波器)

ButterWorthFIlter(巴特沃斯滤波器)

一、背景

这种滤波器最先由英国工程师斯蒂芬·巴特沃斯（Stephen Butterworth）在1930年发表在英国《无线电工程》期刊的一篇论文中提出的。

二、特点

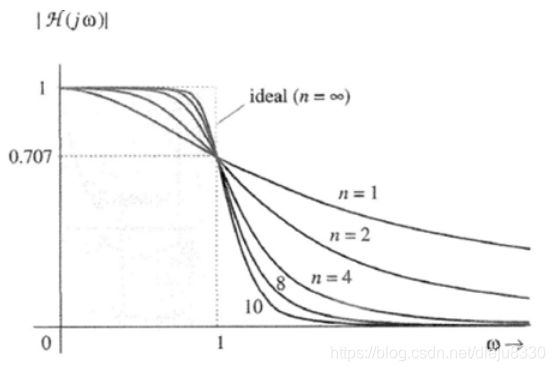
巴特沃斯滤波器的特点是通频带内的频率响应曲线最大限度平坦，没有起伏，而在阻频带则逐渐下降为零。 在振幅的对数对角频率的波特图上，从某一边界角频率开始，振幅随着角频率的增加而逐步减少,趋向负无穷大。一阶巴特沃斯滤波器的衰减率为每倍频6分贝，每十倍频20分贝。二阶巴特沃斯滤波器的衰减率为每倍频12分贝、三阶巴特沃斯滤波器的衰减率为每倍频18分贝、如此类推。巴特沃斯滤波器的振幅对角频率单调下降，并且也是唯一的无论阶数，振幅对角频率曲线都保持同样的形状的滤波器。只不过滤波器阶数越高，在阻频带振幅衰减速度越快。其他滤波器高阶的振幅对角频率图和低阶数的振幅对角频率有不同的形状。

由图可见，当N趋于无穷时，将会得到一个理想的低通滤波器

三、原理

1. 幅值平方

$$|H_a(jw){|}^2=\frac{1}{1+(\frac{w}{wc}{)}^{2N}}$$

2. 拉普拉斯变换

令
$$s=\sigma +j\omega$$
其中，
$$\sigma =0$$
所以有，
$$w=\frac{s}{j}$$
重新带入幅值平方
$$|H(s){|}^2=\frac{1}{1+(\frac{-s^2}{w{c}^2}{)}^N}$$

$$H(s)=\frac{{\omega }_c^N}{a_0{\omega }_c^N+a_1{\omega }_c^{N-1}s+...a_{n-1}{\omega }_c^1{s}^{n-1}+s^N}$$
其中，
$$a_0=1$$
设数组sb的各个元素为上式分母中关于s的幂次方项的系数
$$sb=\{sb[0],sb[1],...sb[N]\}=\{a_0{\omega }_c^N,a_1{\omega }_c^{N-1},...a_{n-1}{\omega }_c^1,1\}$$

3. Z域变换（离散化）

由
$$z=e^{sT}=\frac{e^{\frac{sT}{2}}}{e^{\frac{-sT}{2}}}$$
得到
$$s=\frac{1}{T}lnz$$

3.1 线性化

试图使用泰勒公式对s进行展开，但是lnz在z=0处没有定义，于是令
$$z^{{}^{\prime }}=\frac{z-1}{z+1}$$
于是
$$z=\frac{1+z^{{}^{\prime }}}{1-z^{{}^{\prime }}}$$
对上式在z‘=0处泰勒展开，有
$$\ln z=\ln \frac{1+z^{{}^{\prime }}}{1-z^{{}^{\prime }}}=2(z^{{}^{\prime }}+\frac{1}{3}{z}^{{}^{\prime }3}+\frac{1}{5}{z}^{{}^{\prime }5}...)$$
带入s的定义，整理，得到
$$s=\frac{1}{T}lnz=\frac{2}{T}(\frac{z-1}{z+1}+\frac{1}{3}{\frac{z-1}{z+1}}^3+\frac{1}{5}{\frac{z-1}{z+1}}^5...)$$
取一阶近似，最终得到
$$s=\frac{1}{T}lnz=\frac{2}{T}(\frac{z-1}{z+1})=\frac{2}{T}(\frac{1-z^{-1}}{1+z^{-1}})$$

3.2 双线性变换

双线性变换就是使用这种一阶估计法，将连续时间传递函数H(s)中的s替换成离散域中的z变量
即 $$H_d(z)=H_a(s){|}_{s=\frac{2}{T}(\frac{z-1}{z+1})}=H_a(\frac{2}{T}\frac{z-1}{z+1})$$

进行整理后，最终得到
$$H(z)=\frac{{\omega }_c^N(1+z^{-1}{)}^N}{a_0{\omega }_c^N(\frac{2}{T}{)}^N(1-z^{-1}{)}^N+a_1{\omega }_c^{N-1}(\frac{2}{T}{)}^{N-1}(1-z^{-1}{)}^{N-1}(1+z^{-1}{)}^1+...a_{N-m}{\omega }_c^{N-m}(\frac{2}{T}{)}^{N-m}(1-z^{-1}{)}^{N-m}(1+z^{-1}{)}^m+...a_N(1+z^{-1}{)}^N}$$

最终将上式写成如下：
$$H(z)=\frac{num[0](z^{-1}{)}^0+num[1](z^{-1}{)}^1+...num[N](z^{-1}{)}^N}{den[0](z^{-1}{)}^0+den[1](z^{-1}{)}^1+...den[N](z^{-1}{)}^N}$$
上式中的序列num、den就是离散化的目标。

四、巴特沃斯滤波器的设计（数字滤波器实现）

1.确定参数

需要确定参数如下：

• passF:通带截止频率
• stopF:阻带截止频率
• fs:采样频率
• rp:通带最大衰减
• rs:阻带最小衰减

2.计算预畸参数

双线性变换具有从根本上避免脉冲响应不变法中的频率混叠现象，缺点是引入了频率失真，因此，引入预畸变的概念，即在双线性变换之前，进行预畸来校正频率失真的问题，使得进行双线性变换之后的频率与预期一致。

2.1 预畸原理

由
$$s=\frac{2}{T}(\frac{z-1}{z+1})=\sigma +j\Omega$$
使用下式进行变量代换
$$z=e^{jw}$$
得到
$$\begin{array}{rl}s=& \frac{2}{T}(\frac{z-1}{z+1})\\ =& \frac{2}{T}(\frac{1-e^{-jw}}{1+e^{-jw}})\\ =& \frac{2}{T}(\frac{1-(cos\omega -j\sin \omega )}{1+(cos\omega -j\sin \omega )})\\ =& \frac{2}{T}(\frac{2j\sin \omega }{2+2\cos \omega })\\ =& \frac{2}{T}(\frac{j2\sin \frac{\omega }{2}\cos \frac{\omega }{2}}{4{\cos }^2\frac{\omega }{2}})\\ =& \frac{2}{T}j\tan \frac{\omega }{2}=\sigma +j\Omega \end{array}$$
所以有
$$\begin{array}{rl}\Omega =& \frac{2}{T}\tan \frac{\omega }{2}\\ =& \frac{2}{T}\tan \pi f\end{array}$$

2.2 计算第一步确定的参数预畸值

$$pass\Omega =\tan \frac{\pi \ast passF}{fs}$$
$$stop\Omega =\tan \frac{\pi \ast stopF}{fs}$$

3. 计算低通滤波器阶数

由
$$\begin{array}{r}rp=10\lg (1+(\frac{pass\Omega }{{\Omega }_c}{)}^{2N})\\ rs=10\lg (1+(\frac{stop\Omega }{{\Omega }_c}{)}^{2N})\end{array}$$
可得，阶数N
$$\begin{array}{r}N=\frac{1}{2}=\frac{\lg \frac{10^{0.1rs-1}}{10^{0.1rp-1}}}{\lg \frac{stop\Omega }{pass\Omega }}\end{array}$$

4. 计算截止频率\Omega_c

由
$$\begin{array}{r}rs=10\lg (1+(\frac{stop\Omega }{{\Omega }_c}{)}^{2N})\end{array}$$
有
$$\begin{array}{r}{\Omega }_c=\frac{stop\Omega }{(10^{0.1rs-1}{)}^{\frac{1}{2N}}}\end{array}$$

5. 确定分子分母系数数组长度length

$$length=N+1$$

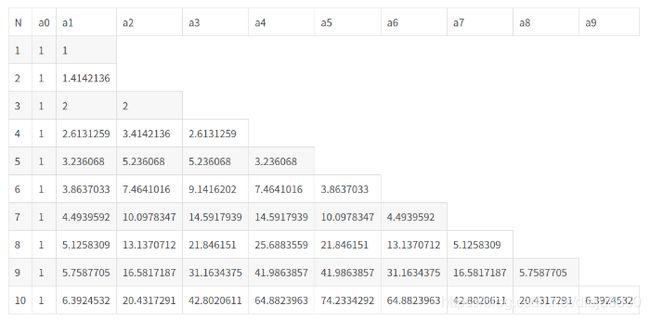
6. 查表，获取拉氏变换下传递函数的分母系数

$$H(s)=\frac{{\Omega }_c^N}{a_0{\Omega }_c^N+a_1{\Omega }_c^{N-1}s+...a_{n-1}{\Omega }_c^1{s}^{n-1}+s^N}$$

即计算:
$$a_0{\Omega }_c^N+a_1{\Omega }_c^{N-1}s+...a_{n-1}{\Omega }_c^1{s}^{n-1}+s^N$$

其中，关于a可查表获得

最终返回数组sb数组sb的各个元素为上式分母中关于s的幂次方项的系数
$$sb=\{sb[0],sb[1],...sb[N]\}=\{a_0{\omega }_c^N,a_1{\omega }_c^{N-1},...a_{n-1}{\omega }_c^1,1\}$$

代码如下：

    for(int i = 0; i < length; i++)
    {
        //a0*Wc^N+a1*Wc^(N-1)*S+....+an-1*Wc^0*S^(n-1)
        returnSb[i] = g_butterPb[length - 1][i] * pow(Wc, length-i); //计算系数
    }
    
    returnSb[length] = 1.0; //最高次幂的系数为1

7. 双线性变换

根据前面得出来的公式：
$$H(z)=\frac{{\omega }_c^N(1+z^{-1}{)}^N}{a_0{\omega }_c^N(\frac{2}{T}{)}^N(1-z^{-1}{)}^N+a_1{\omega }_c^{N-1}(\frac{2}{T}{)}^{N-1}(1-z^{-1}{)}^{N-1}(1+z^{-1}{)}^1+...a_{N-m}{\omega }_c^{N-m}(\frac{2}{T}{)}^{N-m}(1-z^{-1}{)}^{N-m}(1+z^{-1}{)}^m+...a_N(1+z^{-1}{)}^N}$$

7.1 利用杨辉三角计算多项式(1-z^-1)、(1+z^-1)次方项内各自关于(z^-1)的系数

图片来源：https://blog.csdn.net/NDHuaErFeiFei/article/details/88379163

• 对于 (1+z^-1)，
  $$\begin{array}{rl}(z^{-1}+1{)}^1=& 1\ast z^{-1}+1\ast 1\\ (z^{-1}+1{)}^2=& 1\ast (z^{-1}{)}^2+2\ast z^{-1}+1\ast 1\\ (z^{-1}+1{)}^3=& 1\ast (z^{-1}{)}^3+3\ast (z^{-1}{)}^2+3\ast z^{-1}+1\ast 1\end{array}$$

以3次方为例，杨辉三角函数输出[1,3,3,1]

• 对于 (1-z^-1)=(-z^-1+1)
  $$\begin{array}{rl}(-z^{-1}+1{)}^1=& -1\ast z^{-1}+1\ast 1\\ (-z^{-1}+1{)}^2=& 1\ast (z^{-1}{)}^2-2\ast z^{-1}+1\ast 1\\ (-z^{-1}+1{)}^3=& -1\ast (z^{-1}{)}^3+3\ast (z^{-1}{)}^2-3\ast z^{-1}+1\ast 1\end{array}$$

以3次方为例，杨辉三角函数输出[-1,3,-3,1]

杨辉三角函数代码:

/*======================================================================
 * 函数名：  pascalTriangle
 * 函数功能：计算杨辉三角的第N行的值（数组），该系列值为(x+1)^N的系数，
 *         加改进(x-1)^N的系数
 *
 * 变量名称：
 *          N      - 杨辉三角第N行，N=0,1,...,N
 *          symbol - 运算符号，0——(x+1)^N，1——(x-1)^N
 *          vector - 返回数组，杨辉三角的第N行的值
 *
 * 返回值：  void
 *=====================================================================*/
void pascalTriangle(
		int		N,
		int		symbol,
		int		*vector)
{
    vector[0] = 1;
    if(N == 0)
    {
        return;
    }
    else if (N == 1)
    {
        if(symbol == SYMBOL_ADD)
        {
            vector[1] = 1;
        }
        else
        {
            vector[0] = -1; //如果是减号，则第二项系数是-1
            vector[1] = 1;
        }
        return;
    }
    int length = N + 1; //数组长度

	int *temp = (int *)malloc(sizeof(int) * length);
	/*
    int temp[length];   //定义中间变量
    */
    
    temp[0] = 1;
    temp[1] = 1;
    
    for(int i = 2; i <= N; i++)
    {
        vector[i] = 1;
        for(int j = 1; j < i; j++)
        {
            vector[j] = temp[j - 1] + temp[j]; //x[m] = x[m-1][n-1] + x[m-1]
        }
        if(i == N) //最后一次不需要给中间变量赋值
        {
            if(symbol == SYMBOL_SUB) //运算符为减号
            {
                for(int k = 0; k < length; k++)
                {
                    vector[k] = vector[k] * pow((float)-1, length - 1 - k);
                }
            }
            return;
        }
        for(int j = 1; j <= i; j++)
        {
            temp[j] = vector[j];
        }
    }

	if (temp != NULL)
		free(temp);
}

具体实现：

for(int i = 0; i <= length; i++)
{
    for(int j = 0; j<= length; j++)
    {
        tempCoef1[j] = 0;     //tempCoef1和tempCoef2进行初始化
        tempCoef2[j] = 0;
    }
    
    //i ：1 - z^(-1)幂次数
    //otherN : 1 + z^(-1)幂次数
    otherN = length - i;

    pascalTriangle(3, SYMBOL_SUB, tempCoef1);      //利用杨辉三角计算1 - z^(-1)幂的系数
    pascalTriangle(otherN, SYMBOL_ADD, tempCoef2); //利用杨辉三角计算1 + z^(-1)幂的系数

    coefficientEquation(tempCoef1, i+1, tempCoef2, otherN+1); //两个多项式相乘，求其系数
}

7.2 利用杨辉三角计算(1-z^-1)^{N-m}*(1+z^-1)^{m}多项式关于z^-1项的系数

最终的系数数组长度:L=N-m+1+m+1-1=N+1

计算的目标多项式：
$$(1-z^{-1}{)}^{N-m}(1+z^{-1}{)}^m$$

最终得到如下形式：
$$C_0(z^{-1}{)}^N+C_1(z^{-1}{)}^{N-1}+...+C_N(z^{-1}{)}^0$$

返回：
return [C0,C1,C2…CN]

核心函数coefficientEquation()实现两个系数数组相乘后得到的多项式数组

/*======================================================================
 * 函数名：  coefficientEquation（整数）和coefficientEquation2（浮点数）
 * 函数功能：计算多项式相乘的系数
 *
 * 变量名称：
 *          originalCoef - 原来的系数数组，计算后的系数也存储在该数组内
 *          N            - 上面系数对应的多项式系数个数
 *          nextCoef     - 与原数组相乘的数组的系数
 *          nextN        - 上面系数对应的多项式系数个数
 *
 * 返回值：  void
 *=====================================================================*/
void coefficientEquation(
		int		*originalCoef,
		int		N,
		int		*nextCoef,
		int		nextN)
{
    int *tempCoef = (int *)malloc(sizeof(int) * (N+nextN-1));
	/*
    double tempCoef[N + nextN - 1];    //中间变量
    */
    for(int i = 0; i < N + nextN - 1; i++)
    {
        tempCoef[i] = originalCoef[i]; //中间变量初始化
        originalCoef[i] = 0;
    }
    
    //乘完之后有多少项= N + nextN - 1
    //设 (1,2,3) ===>N=3
    //   (3,4,5) ===>nextN=3
    // original[0]=1*3              | (z^-1)^4
    // original[1]=2*3+1*4          | (z^-1)^3
    // original[2]=3*3+2*4+1*5      | (z^-1)^2
    // original[3]=2*5+3*4          | (z^-1)^1
    // original[4]=3*5              | (z^-1)^0
    for(int j = 0; j < nextN; j++)
    {
        for(int i = j; i < N + nextN - 1; i++)
        {
            //printf("%d %d ",tempCoef[i-j],nextCoef[j]);
            originalCoef[i] += tempCoef[i-j] * nextCoef[j];
            //printf("%d %d \n",originalCoef[i],i);
        }
    }
	if (tempCoef != NULL)
		free(tempCoef);
}

7.3 计算H(z)分母系数

分母形式:
$$den[0](z^{-1}{)}^0+den[1](z^{-1}{)}^1+...den[N](z^{-1}{)}^N$$

其中,
$$\begin{array}{rl}den[0]=& (\frac{2}{T}{)}^0\ast C_N\ast sb[0]+(\frac{2}{T}{)}^1\ast C_N\ast sb[1]+...+(\frac{2}{T}{)}^N\ast C_N\ast sb[N]\end{array}$$

$$\begin{array}{rl}den[1]=& (\frac{2}{T}{)}^0\ast C_{N-1}\ast sb[0]+(\frac{2}{T}{)}^1\ast C_{N-1}\ast sb[1]+...+(\frac{2}{T}{)}^N\ast C_{N-1}\ast sb[N]\end{array}$$

$$......$$

$$\begin{array}{rl}den[N]=& (\frac{2}{T}{)}^0\ast C_0\ast sb[0]+(\frac{2}{T}{)}^1\ast C_0\ast sb[1]+...+(\frac{2}{T}{)}^N\ast C_0\ast sb[N]\end{array}$$

最终计算结果：
return [den[0],den[1], … den[N]]

实现代码：

//分母
length=N;
for(int i = 0; i <= length; i++)
{
    for(int j = 0; j <= length; j++)
    {
        denominator[j] += pow(Fsx2, i) * (float)tempCoef1[length - j] * sb[i];
    }
}

7.4 计算H(z)分子系数

(1)如7.2一样，由杨辉三角计算得到(1+z^-1)^N的系数[tmpC0,tmpC1, … tmpCN]
(2)分子形式:

根据双线性变换得到的分子：

$${\omega }_c^N(1+z^{-1}{)}^N$$

可以写成如下形式：

$$num[0](z^{-1}{)}^0+num[1](z^{-1}{)}^1+...num[N](z^{-1}{)}^N$$

其中，

$$\begin{array}{rl}num[0]=& tmp{C}_N\ast sb[0]\end{array}$$

$$\begin{array}{rl}num[1]=& tmp{C}_{N-1}\ast sb[0]\end{array}$$

$$......$$

$$\begin{array}{rl}num[N]=& tmp{C}_0\ast sb[0]\end{array}$$

(3)实现代码:

length=N;
for(int i = 0; i <= length; i++)
{
    //分子系数
    if(i == 0)
    {
        for(int j = 0; j <= length; j++)
        {
            numerator[j] = sb[0] * tempCoef2[length - j];
        }
    }
}

7.5 系数归一化（分子分母同除）

目标：使分母常数项=1

即：
num=num/den[0]
den=den/den[0]

实现代码：

length=N;
for(int i = 0; i <= length; i++)
{
    //系数归一化，分母的常数项为1
    for(int i = length; i >= 0; i--)
    {
        numerator[i] = numerator[i] / denominator[0];
        denominator[i] = denominator[i] / denominator[0];
    }
}

7.6 设计完成

得到了num和den数组，即得到如下形式的H(z)
$$H(z)=\frac{num[0](z^{-1}{)}^0+num[1](z^{-1}{)}^1+...num[N](z^{-1}{)}^N}{den[0](z^{-1}{)}^0+den[1](z^{-1}{)}^1+...den[N](z^{-1}{)}^N}$$